23.3. Верхние и нижние суммы Дарбу

    Пусть функция f определена на отрезке [a,b],  - разбиение этого отрезка, _k = [x_k-1,x_k],
x_k = x_k - x_k-1. Положим

		k = 1, 2, ..., ,	(23.5)
			(23.6)

    Сумма , называется верхней, а сумма - нижней суммой Дарбу функции f. Очевидно, что в случае, когда  функция f ограничена, то нижние m_k и верхние грани M_k (23.5) конечны, и потому суммы Дарбу (23.6) при любом разбиении принимают конечные значения. В дальнейшем будем предполагать, что функция f ограниченна - это естественно, так как нас будут интересовать свойства интеграла от функции f, а он, согласно теореме 1, может существовать только в том случае, когда функция ограниченна. Из того, что выполняется неравенство m_k < M_k, k = 1, 2, ..., , следует, что при любом разбиении выполняется неравенство

    Очевидно также, что в силу определения (23.5) чисел m_k и M_k для любых _{k k} имеет место неравенство

m_k <  f(_k) < M_k,    k = 1, 2, ..., .

Отсюда следует справедливость неравенства

<

< .

(23.8)

    Отметим еще следующие свойства сумм Дарбу.
    1^o. Каждая нижняя сумма Дарбу не превосходит любой верхней:

( ₁ и ₂ - разбиения отрезка [a,b]).
Пусть сначала * , , - разбиения отрезка [a,b],

k = [xk-1,xk],

    Условие * означает, что каждый отрезок _k разбиения является объединением некоторых отрезков разбиения *. Обозначим эти отрезки , тогда , где суммирование ведется по всем таким индексам j_k, что _k . Отсюда следует, что

Кроме того, выполняются неравенства

так как при переходе от отрезка _k к содержащемуся в нем отрезку  нижняя грань значений функции может только увеличиваться.
    Теперь легко доказать неравенство

В самом деле,

Аналогично доказывается неравенство

Пусть теперь ₁ и ₂ - два произвольных разбиения отрезка [a,b]. Возьмем какое-либо разбиение , вписанное в разбиения ₁ и ₂, т. е. ₁ и ₂ . Тогда неравенство (23.9) вытекает из следующей цепочки неравенств:

    2^o. Нижняя (верхняя) сумма Дарбу является нижней (верхней) гранью интегральных сумм Римана, соответствующих данному разбиению:

Пусть  - разбиение отрезка [a,b] и _{k k} = [x_k-1,x_k] , k = 1, 2, ..., . Тогда в силу того, что нижняя грань арифметической суммы числовых множеств равна сумме нижних граней этих множеств, и того, что положительный постоянный множитель можно внести под знак нижней грани (п. 4.3*), получим

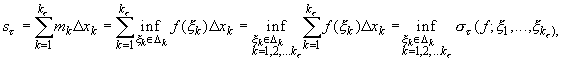
т. е. равенство (23.14) доказано. Аналогично доказывается равенство (23.15). 

    3^o. Имеет место равенство

где _k(f) - колебание функции f на отрезке [x_k-1,x_k] разбиения , k = 1, 2, ..., (см. п. 7.4).
Формула (23.16) следует из того, что для любого множества X Rⁿ справедливо равенство

sup(X - X) = (x' - x) = sup X - inf X,

т. е. разность верхней и нижней граней двух множеств (в данном случае одного и того же) равна верхней грани разности этих множеств (п. 4.3*). В самом деле, так как

M_k - m_kf(x) - f(x) = [f(x') - f(x)] = _k(f),
k = 1, 2, ..., ,

то

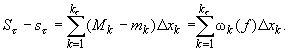
    При заданной на отрезке [a,b] ограниченной функции f верхние и нижние суммы Дарбу являются функциями, заданными на множестве {} всех разбиений отрезка [a,b]. Для таких функций можно определить их предел по аналогии с понятием предела интегральных сумм Римана.
    Пусть на множестве {} всех разбиений отрезка [a,b] задана функция F: F() R.
    Определение 3. Число A назовем пределом функции F() при ||0, если для любой последовательности {_n} разбиений _n отрезка [a,b] такой, что |_n| = 0 , имеет место

F() = A.

    Если A - предел функции F() при ||0, то пишут

    Определение предела (23.17) можно сформулировать и на "языке -".
    Определение 4. Число A называется пределом функции F(x) при ||0, если для любого > 0 существует такое > 0, что для всех разбиений отрезка [a,b], имеющих мелкость || < , выполняется неравенство

|F() - A| < .

    Поскольку определения предела (23.17) так же, как и определения предела интегральных сумм (23.1), могут быть сформулированы в терминах пределов последовательностей, то на эти пределы переносятся обычные свойства пределов, в частности возможность предельного перехода в неравенствах.
    В смысле предела (23.17) мы и будем в дальнейшем говорить о пределах нижних и верхних сумм Дарбу: и .

Ограниченность интегрируемых функций  Оглавление    Нижний и верхний интегралы