28.2. Вычисление площадей в полярных координатах

    Пусть P - замкнутое множество, граница которого состоит из некоторой кривой, заданной уравнением в полярных координатах = (), <  < (() - непрерывная функция), и двух отрезков (которые могут превращаться в точки) лучей = и = (рис. 112), т. е.

P = {(, ):  <  < ,  0 < < ()}.

    Найдем формулу для вычисления площади S = P множества P.
Возьмем какое-либо разбиение отрезка [,] и положим

_k = [_k-1,_k],   _k = _k - _k-1,
 
= {(x, y):  x_k-1 <  x < x_k,  0 < y < m_k},
= {(x, y):  x_k-1 <  x < x_k,  0 < y < M_k},
k = 1, 2, ..., .
= ,  = .

    Множества и представляют собой круговые секторы с углом _k и радиусами соответственно m_k и M_k, а и  - ступенчатые фигуры, составленные из указанных секторов и соответственно содержащиеся в множестве P и содержащие его: P . Из этих включений следует, что

Согласно формуле для площади сектора

= ,   = ,

поэтому

= = ,   = = ,

Получившиеся суммы являются соответственно нижней и верхней  суммами Дарбу функции
²():  = , = . Таким образом, в силу (28.14)

Поскольку суммы Дарбу и при ||0 стремятся к одному и тому же пределу - интегралу от функции
²() :

 = = ²()d,

то из неравенств (28.15) следует, что

    Пример. Найдем площадь S множества, ограниченного кривой

= a(1 + cos),   0 < < 2

(она называется кариотидой; рис. 113):

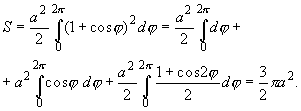
Вычисление площадей криволинейных трапеций  Оглавление   Вычисление длины кривой