S = s(b) - s(a)
= 
s'(t) dt = |r'(t)| dt
(s(a) = 0).
(28.17)
Применение определенного интеграла
к задачам вычисления площадей множеств было
основано на его равенстве пределу интегральных
сумм. Приведем теперь пример применения
определенного интеграла, который основан на
формуле Ньютона-Лейбница, позволяющий найти
значение функции, если известна ее производная.
Пусть Г - кривая, заданная своим
непрерывно дифференцируемым векторным
представлением r = r(t), a < t < b;
тогда она спрямляема, и если s = s(t) -
ее переменная длина дуги, отсчитываемая от
начала, то функция s(t) дифференцируема и
s'(t) = |r'(t)|. По
формуле Ньютона-Лейбница для длины S = s(b)
кривой имеем формулу
S = s(b) - s(a)
= |
(28.17) |
Если r'(t) = (x(t), y(t), z(t)), то
|
(28.18) |
В случае, когда кривая Г является графиком функции y = f(x), a < x < b, для ее длины S в силу (28ю18) справедлива формула
|
(28.19) |
|
Пример. Вычислим длину астроиды
x = a cos3 t, y = a sin3 t
(рис. 114). В силу симметричности астроиды
относительно координатных осей ее длина S
равна учетверенной длине ее части, лежащей в
первом координатном угле, т. е.
соответствующей изменению параметра на
отрезке [0,
/2]. Заметив, что
x' = -3a cos2 t sin t, y' = 3a sin2 t cos t,
согласно формуле (28.18), в которой надо положить z' = 0, получим
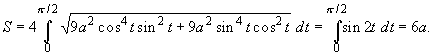
Вычисление площадей в полярных координатах Оглавление Площадь поверхности вращения
