28.1. Вычисление площадей криволинейных трапеций

    Теорема1. Если функция f неотрицательна и интегрируема на отрезке [a,b], a

P = {(x, y):  a <  x < b,  0 < y < f(x)},

(28.1)

то площадь P множества S выражается формулой

S =  f(x)dx.

(28.2)

Рис. 108
Рис. 108

    Множество вида (28.1) называется криволинейной трапецией, порожденной графиком функции f (рис. 108).
начало Пусть - разбиение отрезка [a,b],

дельтаk = [xk-1,xk],  дельтаxk = xk - xk-1,

k = 1, 2, ..., .

(28.3)

    Обозначим соответственно через и замкнутые прямоугольники, составленные из всех прямоугольников вида

= {(x, y):  xk-1 <  x < xk,  0 < y < mk},

(28.4)

= {(x, y):  xk-1 <  x < xk,  0 < y < Mk},

(28.5)

т. е.

= ,  = .

(28.6)

    Из (28.3) следует, что для любого разбиения tau выполняется включение включает P включает , а следовательно (см. теорему в п. 27.1),

mu < muP  < mu.

(28.7)

Из (28.4) и (28.5) следует, что mu = mkдельтаxk, mu = Mkдельтаxk , и так как прямоугольники , соответственно , не имеют общих внутренних точек, то в силу (28.6)

mu = mu = mkдельтаxk = ,

(28.8)

mu = mu = Mkдельтаxk = .

(28.9)

Иначе говоря, площади многоугольников и равны соответственно нижней и верхней суммам Дарбу функции f (рис. 109). Поэтому из неравенства (28.7) следует, что

< muP  < .

(28.10)

А так как = =  f(x)dx, то muP =  f(x)dx. конец

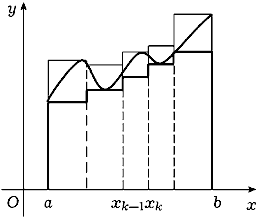Рис. 109
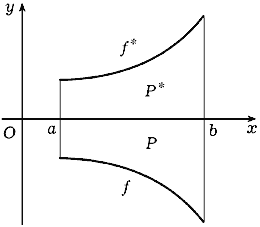Рис. 109		 Рис. 110
Рис. 110

    Если функция f неположительна и непрерывна на отрезке [a,b] и

P = {(x, y):  a <  x < b,  f(x) < y < 0},

то

muP = - f(x)dx.

(28.11)

начало     Действительно, если

f*(x) определение -f(x),    x принадлежит [a,b],

(28.12)

а P* - множество, симметричное с множеством P относительно оси x (рис. 110), то в силу формулы (28.2)

muP* =  f*(x)dx,

(28.13)

ибо функция f* уже неотрицательна. Поскольку площади симметричных множеств равны, т. е. muP* =muP, а

 f*(x)dx - f*(x)dx,

то из равенства (28.13) сразу следует формула (28.11). конец
    Если функция f непрерывна и знакопеременна на отрезке [a,b], то интеграл от нее равен "алгебраической сумме", вообще говоря, бесконечного числа слагаемых, равных площадям криволинейных трапеций, образованных частями графика функции f, расположенными соответственно в полуплоскостях y > 0 и y < 0, причем площади первых берутся со знаком плюс, а площади вторых - со знаком минус.

Рис.111
Рис.111

    Примеры.
    1. Найдем площадь, образованную одной аркой синусоиды:

sin x dx = -cos x = 2.

    2. Найдем площадь S(x) криволинейной трапеции, ограниченной дугой гиперболы y = 1/x, отрезком [1,x] оси x и соответствующими отрезками, параллельными оси y (рис. 111):

S(x) = = ln t = ln x.

Понятие объема  Оглавление  Вычисление площадей в полярных координатах