28.4. Площадь поверхности вращения

    Пусть на отрезке [a,b] задана неотрицательная функция y = f(x):

f(x) > 0,   a < x < b.

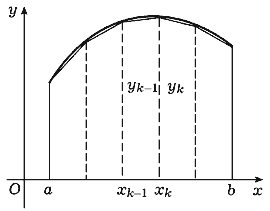
    Множество, получающееся вращением графика функции f(x) вокруг оси Ox, называется поверхностью вращения (этого   графика). Определим ее площадь. Пусть - какое-либо разбиение отрезка [a,b]. Впишем в график функции f ломаную , соответствующую разбиению , т. е. ломаную с вершинами в точках (x_k, y_k), где

(рис. 115). Звено этой ломанной с концами в точках (x_k-1, y_k-1) и (x_k, y_k) (будем называть его k-м звеном ломаной ) при вращении его вокруг оси x описывает боковую поверхность усеченного конуса ( в частности, при y_k-1 = y_k - боковую поверхность цилиндра), площадь которой равна

где y_k-1 и y_k-1 - соответственно радиусы оснований усеченного конуса, а - длина его образующей, x_k = x_k - x_k-1 , y_k = y_k - y_k-1, k = 1, 2, ..., . Поэтому площадь поверхности , получающейся от вращения ломаной вокруг оси Ox, выражается формулой

    Если существует предел , то он называется  площадью поверхности вращения, образованной вращением графика функции вокруг оси x. Таким образом, обозначив через L площадь указанной поверхности вращения, будем иметь

Пусть теперь функция f непрерывно дифференцируема на отрезке [a,b]; тогда для площади поверхности можно получить удобную для вычислений формулу в виде некоторого интеграла.

    Теорема 2. Если функция f непрерывно дифференцируема и неотрицательна на отрезке [a,b], то для площади поверхности вращения, образованной вращением графика функции f вокруг оси Ox, имеет место формула

L = 2 f(x)dx.

    Функция f непрерывно дифференцируема на отрезке [a,b], т. е. ее производная непрерывна, и, следовательно, ограничена на этом отрезке. Это означает, что существует такая постоянная c > 0, что для всех точек x [a,b] выполняется неравенство

По формуле конечных приращений Лагранжа имеем

y_k = y_k - y_k-1 = f'(_k)x_k,     x_k-1 < _k < x_k,    k = 1, 2, ..., .

Поэтому = x_k, откуда

Эта сумма не является интегральной, так как в ней значения y_k-1 = f(x_k-1), y_k = f(x_k) и f'(_k) берутся в разных точках x_k-1, x_k-1 и _k отрезка [x_k-1,x_k] разбиения . Сравним ее с интегральной суммой

функции 2f(x). Снова применив формулу Лагранжа, получим

Теперь имеем

Поэтому

|-|[(f(_k) - y_k-1) - (y_k - f(_k))]x_k <
< (| f(_k) - y_k-1)| - | y_k - f(_k)|)x_k2c||x_k = 2c(b - a)||.

Отсюда следует, что

Но является интегральной суммой функции 2y, где y = f(x), поэтому

И так как в силу формулы (28.29) = , то для площади L поверхности вращения получается формула

    Вспоминая, что dx = ds (см. п. 17.3), т. е. является дифференциалом длины дуги, формулу (28.31) для площади поверхности вращения можно записать в более компактном виде

    Можно показать, что эта формула остается справедливой для площади поверхности вращения, образованной вращением вокруг оси x любой непрерывно дифференцируемой кривой, заданной параметрическим представлением x = x(t), y = y(t),  a < t < b, и не пересекающей ось x. В этом случае в развернутом виде формула (28.32) имеет вид

Пример. Найдем площадь L поверхности, полученной вращением вокруг оси x одной арки синусоиды y = sin x. Согласно формуле (28.31) имеем

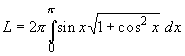
Интеграл, стоящий в правой части этого равенства, был вычислен раньше (пример 2 в п. 26.2), он равен
ln(1 + ) + . Поэтому сразу находим значение искомой площади

L = 2(ln(1 + ) + ).

Вычисление длины кривой  Оглавление   Объем тел вращения