30.1. Определение ряда

    Определение1. Пара последовательностей {u_n} и {s_n}, где u_n, s_n C, n = 1, 2, ...,

называется рядом (а также бесконечной суммой) и обозначается

u₁ + u₂ + ... + u_n + ...

или

    Элементы последовательности {u_n} называются членами ряда, а элементы последовательности {s_n} - его частичными суммами.
    Если существует конечный предел

то он называется суммой ряда. В этом случае ряд называется сходящимся и пишут

u_n = s.

    Если последовательность частичных сумм {s_n} не стремится к конечному пределу, то ряд (30.2) называется расходящимся.
    Очевидно, что

    Из формул (30.1) и (30.4) видно, что каждая из последовательностей {u_n} и {s_n} однозначно определяет другую. Таким образом, чтобы задать ряд (30.2), достаточно задать одну из последовательностей {u_n} или {s_n}. В этом смысле изучение рядов равносильно изучению последовательностей.
    Часто нумерацию членов ряда производят не натуральными числами, а целыми, начиная с нуля, т. е. числами 0, 1, 2, ..., а иногда - начиная с некоторого целого n₀, т. е. числами n₀, n₀ + 1, ...  
    Примеры.
   1. Примером сходящегося ряда является ряд

членами которого являются элементы геометрической прогрессии {qⁿ}, q C, |q|. В самом деле, в этом случае

s_n q^k = ,    n = 1, 2, ...,

и потому

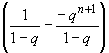s_n = = = - qⁿ = .

Следовательно, ряд (30.5) при |q| < 1 сходится и

qⁿ  = .

    2. Примером расходящегося ряда является ряд, все члены которого равны единице: u_n = 1, n = 1, 2, ... В этом случае s_n = 1 = n, поэтому

s_n = +.

Оглавление  Интегралы от комплекснозначных функций действительного аргумента  Оглавление  Свойства сходящихся рядов