30.3. Критерий Коши

    Теорема 4 (критерий Коши сходимости ряда). Для того чтобы ряд u_n сходился, необходимо и достаточно, чтобы для любого > 0 существовало такое n₀, что для всех n > n₀ и всех целых p > 0 имеет место неравенство

    Это утверждение сразу следует из критерия Коши существования конечного предела последовательности, примененного к последовательности частичных сумм {s_n} данного ряда, ибо

u_n +  u_n+1 + ... + u_n+p = s_n+p -  s_n-1. 

    Замечание. При p = 0 из теоремы следует, что если ряд u_n сходится, то для любого > 0 существует такой номер n₀, что для всех n > n₀ выполняется неравенство |u_n| < , а это означает, что u_n = 0. Таким образом, мы получим еще одно доказательство необходимого условия сходимости ряда (см. теорему 1).

    Пример. Рассмотрим ряд

называемый гармоническим, и докажем, что он расходится.
    При любом натуральном n имеем

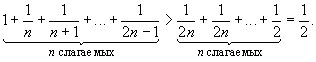
Поэтому если 0 < < 1/2 , то для ряда (30.10) нельзя подобрать номера n₀, указанного в критерии Коши, так как при любом n = 1, 2, ... и p = n - 1 не выполняется условие (30.9). Следовательно, гармонический ряд расходится.
    Отметим, что последовательность {1/n} членов гармонического ряда стремится к нулю:

(1/n) = 0.

    Таким образом, условие стремления к нулю последовательности членов ряда, являсь необходимым условием сходимости ряда, не является достаточным для этого.

Свойства сходящихся рядов  Оглавление  Признаки сходимости рядов с неотрицательными членами