30.4. Признаки сходимости рядов с неотрицательными членами

    Лемма 1. Если члены ряда неотрицательны, то он сходится тогда и только тогда, когда его частичные суммы ограничены сверху.
    Если члены ряда

неотрицательны (u_n > 0, n = 1, 2, ...) , то

т. е. последовательность частичных сумм {s_n} данного ряда возрастает, а возрастающая последовательность имеет конечный предел тогда и только тогда, когда она ограничена сверху. 
    Замечание 1. Если члены ряда (30.11) неотрицательны, то последовательность его частичных сумм {s_n}, согласно (30.12), возрастает и, следовательно, всегда имеет конечный или бесконечный предел s, причем

и поэтому

Если s+, то пишут u_n = +.
    Замечание 2. Ряд с неотрицательными членами сходится тогда и только тогда, когда сходится по крайней мере одна подпоследовательность последовательности его частичных сумм. Действительно, последовательность частичных сумм ряда с неотрицательными членами возрастает и потому всегда имеет конечный или бесконечный предел, совпадающий, конечно, с пределом любой ее подпоследовательности.
     Теорема 5 (интегральный признак Коши сходимости ряда). Если функция f неотрицательна и убывает на полупрямой x > 1, то для того чтобы ряд

сходился, необходимо и достаточно, чтобы сходился интеграл

    В силу монотонности функции f на промежутке [1,+] она интегрируема по Риману на любом конечном отрезке (1,], [1,+), и потому имеет смысл говорить о несобственном интеграле (30.16).
    Если

k < x < k + 1,   k = 1, 2, ...,

то в силу убывания функции  будем иметь

f(k) >  f(x) >   f(k + 1).

Проинтегрировав это неравенство по отрезку длины 1 (рис. 122), получим

f(k)dx >  f(x)dx >  f(k + 1)dx,

т. е.

f(k) >  f(x)dx >  f(k + 1).

Просуммировав получившиеся неравенства по k от 1 до n, придем к основному неравенству

f(k + 1) < f(x)dx < f(k),

т. е. к неравенству

где

s_n = f(k),    n = 1, 2, ...

Если интеграл f(x)dx сходится, то из неравенства (30.17) в силу неотрицательности подынтегральной функции следует, что

а поэтому последовательность частичных сумм s_n, n = 1, 2, ..., ряда (30.13) с неотрицательными членами ограничена сверху числом  f(1) + f(x)dx. Отсюда согласно лемме 1 следует, что этот ряд сходится.
    Если же интеграл f(x)dx расходится, то в силу неотрицательности подынтегральной функции f(x) имеем

а так как согласно неравенству (30.17)

s_n >  f(x)dx,

то, перейдя к пределу в этом неравенстве при x, получим s_n+. Это означает, что ряд (30.13) расходится. 
    Для применения интегрального признака к исследованию сходимости ряда u_n с неотрицательными членами надо подобрать такую убывающую функцию f, что f(n) = u_n, n = 1, 2, ..., и затем исследовать сходимость интеграла (30.16).
    Применим этот метод к исследованию сходимости рядов вида

В этом случае при > 0 требуемой функцией, очевидно, является функция . Поскольку интеграл

сходится при > 1 и расходится при < 1, то и ряд (30.20) сходится при > 1и расходится при < 1. Расходимость ряда (30.20) при < 0 ясна непосредственно: последовательность его членов не стремится к нулю, ибо > 1 при < 0.
    Теорема 6 (признак сравнения). Пусть

    Тогда:
    1) если ряд v_n сходится, то и рядu_n сходится;
    2) если ряд u_n расходится, то расходится и ряд v_n.

    Следствие. Пусть u_n > 0, v_n > 0, n = 1, 2, ..., и

    Тогда:
    1) если ряд v_n сходится и 0 < l < +, то сходится и ряд u_n ;
    2) если ряд v_n расходится и 0 < l < +, то расходится и ряд u_n .
    В частности, если = 1, то ряды u_n и v_n сходятся и расходятся одновременно.
    Доказательство теоремы. Если ряд v_n сходится, т. е. имеет конечную сумму

= v_n, _n v_k,

то для любого n = 1, 2, ... выполняется неравенство

Следовательно,

а это в силу леммы означает, что ряд u_n сходится.
    Если ряд u_n расходится, то расходится и ряд v_n, так как если бы он сходился, то в силу уже доказанного сходился бы и ряд u_n . 
    Доказательство следствия. Пусть ряд v_n сходится.
    Поскольку l < +, то в силу условия (30.22) существует такой номер n₀, что для всех n > n₀ выполняется неравенство < l + 1 , а следовательно, и неравенство

    Если ряд v_n сходится, то сходится и ряд (l + 1)v_n (теорема 2), а поэтому по признаку сравнения (теорема 6) в силу неравенства (30.25) сходится и ряд , а тогдa (см. теорему 3) сходится и ряд u_n.
    Пусть ряд v_n расходится. По условию l > 0 ; выберем число l' так, чтобы 0 < l'  < l. В силу условия (30.22) существует такой номер n₀, что для всех n > n₀ выполняется неравенство > l', а следовательно, и неравенство

Поскольку из расходимости ряда v_n вытекает, очевидно, и расходимость ряда l'v_n, то согласно второму утверждению теоремы 6 из неравенства (30.26) следует расходимость ряда , а потому и ряда u_n. 
    Заметим, что при применении признака сравнения для исследования сходимости ряда с неотрицательными членами в качестве ряда, с которым сравнивается данный ряд, часто бывает удобным брать ряд вида .
    Примеры.
    1. Ряд сходится, ибо

0 < < ,  n = 1, 2, ...,

и ряд сходится.
    2. Ряд расходится, ибо

> = ,

и ряд расходится.

    Теорема 7 (признак Даламбера). Пусть для ряда

существует предел

Тогда если l < 1, то ряд (30.27) сходится, а если  l > 1, то расходится.
    Пусть сначала   l < 1. Выберем число q так, чтобы  l < q < 1. Тогда в силу условия (30.28) существует такой номер n₀ > 1, что для всех n > n₀ выполняется неравенство < q и, следовательно, неравенство u_n > qu_n-1. Применяя это неравенство последовательно для , n = n₀ + 1, n₀ + 2, ... получим

,
,
......................................
,
......................................

Но ряд силу условия 0 < q < 1 сходится, поэтому, согласно признаку сравнения, сходится и ряд
, а следовательно, и ряд (30.27).
    Пусть теперь l > 1; тогда в силу условия (30.28) существует такой номер n₀, что для всех n > n₀ выполняется неравенство > 1, а поэтому и неравенство u_n > u_n-1. Применяя его последовательно для n = n₀ + 1, n₀ + 2, ..., получим

u_n+1 > u_n > ... > > > 0.

Поэтому последовательность членов ряда (30.27) не стремится к нулю, откуда и следует его расходимость. 
    Теорема 8 (признак Коши). Пусть для ряда

существует предел

Тогда если l < 1, то ряд (30.29) сходится, а если l > 1, то расходится.
    Пусть сначала l < 1. Выберем число q так, чтобы l < q < 1. Тогда в силу условия (30.30) существует такой номер n₀, что для всех n > n₀ выполняется неравенство u_n^1/n < q и, следовательно, u_n < qⁿ. Поскольку ряд
qⁿ сходится, то сходится ряд , а поэтому и ряд (30.29).
    Если l > 1, то в силу условия (30.30) существует такой номер n₀, что при n > n₀ выполняется неравенство u_n^1/n > 1, т. е. u_n > 1, и, следовательно, последовательность членов ряда (30.29) не стремится к нулю, поэтому этот ряд расходится. 
    Примеры.
    3. Ряд (1/n!) сходится. Это устанавливается, например, с помощью признака Даламбера:

= (1/n) = 0.

    4. Ряд (1/nⁿ) сходится. Это сразу можно установить с помощью признака Коши:

 (1/nⁿ)^1/n = (1/n) = 0.

    5. Для ряда с общим членом  u_n = , > 0, имеем

,

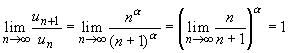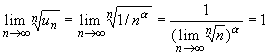
(см. пример 4 в п. 13.2). Таким образом, при применении признаков Даламбера и Коши соответствующие пределы равны единице, т. е. при помощи этих признаков нельзя определить, сходятся или расходятся рассматриваемые ряды. Среди них есть как сходящиеся при > 1, так и расходящиеся при < 1. Иначе говоря, среди рядов u_n с неотрицательными членами, для которых (u_n+1/u_n) = 1, соответственно
(u_n)^1/n = 1, имеются как сходящиеся например, (1/n²), так и расходящиеся например, (1/n) ряды.

Критерий Коши  Оглавление  Знакочередующиеся ряды