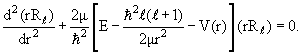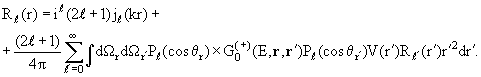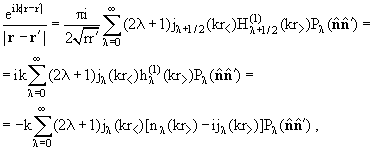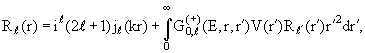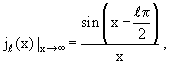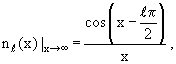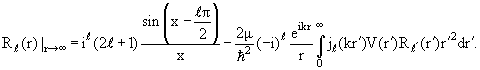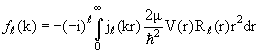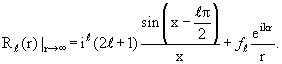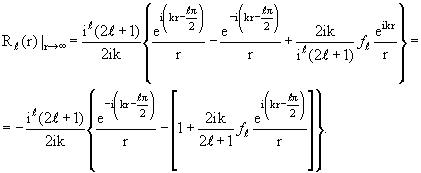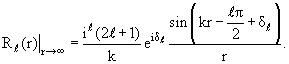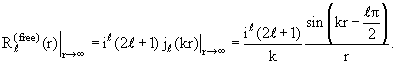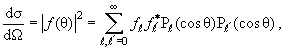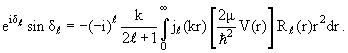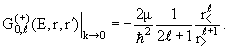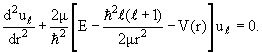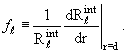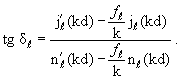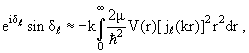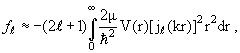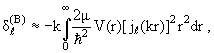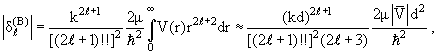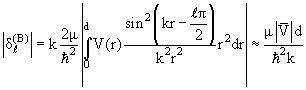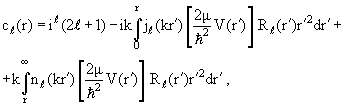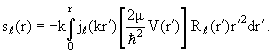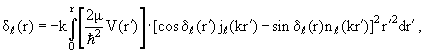Лекция 3. Рассеяние на сферически-симметричном потенциале. Разложение по парциальным волнам

§ 3.1. Дифференциальное и интегральное уравнения для радиальных волновых функций

    В сферически-симметричном поле орбитальный момент частицы сохраняется. Применительно к задаче рассеяния это означает, что если представить падающий поток частиц как совокупность парциальных волн, соответствующих определенным значениям орбитального момента частицы, то каждая такая волна рассеивается на силовом центре независимо от других парциальных волн. С математической точки зрения это создает упрощение задачи, поскольку, решая волновое уравнение для каждой парциальной волны в отдельности, легко разделить переменные волновой функции и, в отличие от общего случая (1.4) или (1.9), свести дело к одномерным дифференциальным или интегральным уравнениям. С физической точки зрения важнейшим новым для нас аспектом при решении задачи рассеяния методом парциальных волн является вопрос о том, как интерферируют между собой разные парциальные волны, попадая в детектор рассеянных частиц. Рассмотрев взаимное поведение парциальных волн на больших расстояниях от рассеивающего центра, мы увидим, что вклад каждой из них в амплитуду рассеяния (а следовательно, в дифференциальное и полное сечения рассеяния) определяется всего лишь одним вещественным параметром − фазой рассеяния. Величина и энергическая зависимость фаз рассеяния определяются видом потенциальной энергии V(r).
    Перейдем к последовательному изложению метода парциальных волн.
    Из симметрийных соображений вполне ясно, что в случае рассеяния частицы сферически-симметричным потенциалом амплитуда рассеяния /(k,k') зависит лишь от модуля импульса
k = |k| = |k'| (т. е. от энергии частицы Е) и от угла Э между векторами k и k' − угла рассеяния. Волновая функция задачи рассеяния (r) удовлетворяет теперь уравнению

(3.1)

где, в отличие от (1.32), вместо V(r') стоит V(r') и поэтому она тоже зависит лишь от r и угла θ_r между k и r, но не зависит от азимутального угла. Представим (r) в виде разложения по полиномам Лежандра от косинуса угла θ_r:

(3.2)

Функции R_ℓ(r) будем называть радиальными функциями задачи рассеяния. Они, конечно, удовлетворяют тому же дифференциальному уравнению − радиальному уравнению Шредингера, что и радиальные волновые функции в задаче о связанных состояниях частицы:

(3.3)

Однако, имея дело с задачей рассеяния, где более тонко стоит вопрос о дополнительных условиях к решению волнового уравнения, удобно наряду с дифференциальным уравнением (3.3) построить также и интегральное уравнение для функции R^(r), соответствующее интегральному уравнению (3.1).
    Для этого подставим (3.2) в (3.1), разложим по парциальным волнам плоскую волну [1, с. 271]:

(3.4)

где j_ℓ(kr) − сферическая функция Бесселя, и, умножив правую и левую части уравнения на P_ℓ(cosθ_r), воспользуемся свойством ортонормированности полиномов Лежандра:

(3.5)

В результате

(3.6)

Воспользуемся вьфажением (1.21) для функции Грина, а также известным в теории специальных функций разложением [3]:

(3.7)

где r_< − меньшее, a r_> − большее из значений r и r', и ' − единичные векторы в направлении векторов r и r', а n_λ(x) − сферическая функция Неймана. Подставляя (3.7) в (3.6) и используя известные формулы

(3.8)

(3.9)

получаем интегральное уравнение для радиальных функций R_ℓ(r) в окончательном виде:

(3.10)

где

(3.11)

функция Грина для ℓ-й парциальной волны свободной частицы.
    Рассмотрим асимптотику радиальных функций R_ℓ(r) при больших r. Для этого нам понадобятся асимптотические выражения сферических функций Бесселя и Неймана, входящих в (3.10) и
(3.11) [1, с. 269]:

(3-12)

(3-13)

Подставляя их в (3.11), получаем

(3.14)

Здесь мы ограничились случаем потенциала конечного радиуса. Введем обозначение

(3.15)

и запишем с его помощью асимптотическое выражение (3.14) более компактно:

(3.16)

Подставляя это выражение в (3.2) и снова используя (3.4), получаем

(3.17)

Отсюда видно, что ƒ_ℓ − это коэффициент разложения амплитуды рассеяния по полиномам Лежандра:

(3.18)

Мы будем называть их парциальными амплитудами рассеяния.

§ 3.2. Фазы рассеяния

    Перестроим асимптотическое выражение (3.16), придав ему вид суперпозиции сходящейся и расходящейся сферических волн:

(3.19)

При движении частиц в поле, описываемом вещественным потенциалом, число частиц сохраняется. Это значит, что на асимптотически большом расстоянии от силового центра (r >> d) интенсивности сходящейся к центру сферической волны e^-ikr/r и расходящейся из центра сферической волны e^ikr/r равны друг другу. В свою очередь это означает, что на коэффициент перед расходящейся волной в (3.19) наложено условие:

(3.20)

    Условие (3.20) позволяет ввести для описания каждой парциальной амплитуды рассеяния ƒ_ℓ(k), являющейся, вообще говоря, комплексной функцией энергии (импульса) частицы, одну вещественную функцию δ_ℓ(k), называемую фазой рассеяния:

(3.21)

To же соотношение полезно записать и по-другому:

(3.22)

    При каждом значении энергии (импульса) частицы фазы рассеяния δ_ℓ полностью определяют асимптотический вид радиальной функции R_ℓ(r) соответствующей парциальной волны. Подставляя (3.21) в (3.19), получаем

(3.23)

Как видно из (3.15), при «выключении» взаимодействия частицы с силовым центром (V→0) обращаются в нуль все парциальные амплитуды рассеяния ƒ_ℓ, а вместе с ними, согласно (3.21), и все фазы δ_ℓ. При этом асимптотическое выражение (3.23) превращается в асимптотику ℓ-й составляющей волновой функции свободной частицы:

(3.24)

Сравнение выражений (3.24) и (3.23), отличающихся фазовым сдвигом в аргументе синуса, позволяет лучше понять смысл термина «фаза рассеяния».
    Выразив через фазы рассеяния  δ_ℓ парциальные амплитуды ƒ_ℓ, мы можем, пользуясь соотношениями (3.18) и (1.41), выразить через них полную амплитуду рассеяния, дифференциальное сечение, а затем и полное сечение рассеяния:

(3.25)

(3.26)

(3.27)

(при получении последней формулы мы воспользовались свойством ортонормированности полиномов Лежандра (3.5)). Формула (3.26) показывает, что угловое распределение рассеянных частиц зависит от интерференции между парциальными волнами с разными значениями орбитального момента частицы. Однако в полном сечении рассеяния а после интегрирования по всем углам вьшета рассеянной частицы эффект интерференции пропадает.
    Сравнение формул (3.25) и (3.27) позволяет установить интересное соотношение между мнимой частью амплитуды рассеяния вперёд и полным сечением рассеяния:

(3.28)

Это так называемая оптическая теорема. Доказанная нами для случая потенциального рассеяния, она (мы увидим это в дальнейшем) справедлива и в общем случае многоканального рассеяния. Мы будем обращаться к оптической теореме как к строгому и модельно независимому соотношению при оценке качества приближенных методов теории столкновений.

§ 3.3. Энергетическая зависимость фаз рассеяния при низких энергиях

    При низких энергиях, когда импульс падающих частиц много меньше обратного радиуса взаимодействия (kd << 1), зависимость фаз рассеяния от энергии носит универсальный характер. Чтобы установить эту зависимость, обратимся сначала к формулам (3.15) и (3.21). Исключив из них ƒ_ℓ(k), получаем

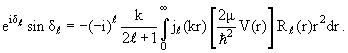(3.29)

Это строгое соотношение, связывающее фазу рассеяния ℓ-й парциальной волны с соответствующей радиальной функцией R_ℓ(r) во внутренней области r < d, аналогично соотношению (1.34) в общей формулировке задачи потенциального рассеяния. Рассмотрим правую часть соотношения (3.29) при kd << 1. Для этого нам понадобятся предельные выражения сферических функций Бесселя и сферических функций Неймана при малых значениях аргумента:

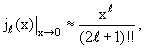(3.30)

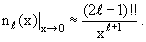(3.31)

Рассматривая с учетом этих свойств функций j_ℓ(х) и n_ℓ(х) соотношение (3.11), видим, что функция Грина 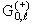(E,r,r') при k → 0 теряет зависимость от энергии (импульса) частицы:

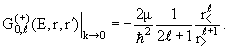(3.32)

Обращаясь теперь к интегральному уравнению (3.10), получаем, что при k → 0 решение этого уравнения R_ℓ(r) ведет себя в зависимости от к так же, как сферическая функция Бесселя j_ℓ(kr), т.е. пропорционально k^ℓ. Следовательно, из (3.29) вытекает

Это и есть искомая зависимость фаз рассеяния от энергии (импульса) частиц при малых энергиях. Она носит универсальный характер и присуща рассеянию на любом потенциале конечного радиуса.

§ 3.4. Методы вычисления фаз рассеяния

    Точное решение задачи рассеяния с целью вычисления фаз рассеяния возможно лишь для отдельных искусственно придуманных потенциалов. На практике, когда приходится иметь дело с реалистическими потенциалами, фазы рассеяния всегда вычисляются приближенно, что связано либо с использованием тех или иных физических аппроксимаций, либо с проведением численного счета. Мы познакомимся с методами и того и другого родов.

а) Метод решения радиального уравнения Шредингера

Перепишем уравнение (3.3) в виде

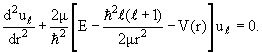(3.34)

Здесь, как и при решении задачи о связанных состояниях частицы [1, с.114], функции u_ℓ(r) связаны с R_ℓ(r) соотношением

и при малых r ведут себя согласно степенному закону:

Поведение u_ℓ(r) при асимптотически больших г получаем из (3.23):

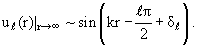(3.37)

    В общем случае уравнение (3.34) интегрируется численно, начиная от r = 0; для «разгонки» численного интегрирования удобно использовать свойство (3.36). Мы не будем вдаваться в чисто вычислительные аспекты этой процедуры. Для нас важно, что задачей интегрирования является построение всего «профиля» функции u_ℓ(r) с выходом при r → ∞ на асимптотику (3.37); при этом должно быть соблюдено условие непрерывности функции u_ℓ(r) и ее первой производной u'_ℓ(r) во всей области 0 < r < ∞.
    При рассеянии на потенциале конечного радиуса (пусть d − размеры области взаимодействия) в задаче имеются два масштаба измерения расстояний r: параметр d и длина волны 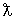= 1/k. Соотношение (3.37), как и соотношение (3.23), из которого оно получено, справедливы, если выполняются два неравенства: kr >> 1, r > d. Если энергия частицы Е и размеры области взаимодействия d таковы, что условие kr >> 1 не выполняется, то асимптотическое поведение (3.37) начинается далеко за границей области взаимодействия (r >> d). В этом случае не рационально доводить численное интегрирование до асимптотически больших значений r >> d, поскольку уже при r > d частица движется свободно и уравнение (3.3) переходит в уравнение движения свободной частицы:

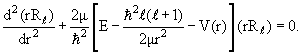(3.38)

При Е > 0 его линейно независимыми решениями являются сферическая функция Бесселя j_ℓ(kr) и сферическая функция Неймана n_ℓ(kr), а общее решение уравнения (3.34) при r > d имеет вид

Вместо констант интегрирования А_ℓ и В_ℓ удобно выбрать две другие:

Следовательно,

С учетом (3.12) и (3.13) отсюда видно, что общее решение (3.39) имеет требуемую асимптотику (3.37).
    Таким образом, практическая задача интегрирования уравнения (3.34) заключается в том, чтобы, начиная с r = 0, выйти в область свободного движения частицы r > d и «сшить» волновую функцию, найденную для внутренней области, с функцией (3.41). Пусть 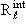(r) = 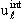/r − решение уравнения (3.3), (3.34), удовлетворяющее условию (3.36) и справедливое во всей внутренней области 0 < r < d. Его «сшивание» с (3.41) означает:

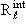(d) = Cℓ{cos δℓ jℓ(kd) − sin δℓ nℓ(kd)}, d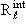/dr|r=d = kCℓ{cos δℓ j'ℓ(kd) − sin δℓ n'ℓ(kd)},

(3.42)

где j'_ℓ(x) ≡ dj_ℓ(x)/dx. Введем логарифмическую производную волновой функции 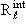(r) на границе области взаимодействия:

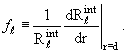(3.43)

Исключая из (3.42) константу C_ℓ (а вместе с ней и произвольно выбираемый при интегрировании уравнения (3.3) нормировочный множитель в 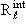(r)), выражаем фазу рассеяния δ_ℓ через логарифмическую производную ƒ_ℓ:

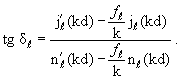(3.44)

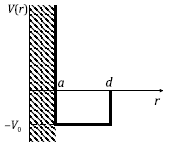
    В качестве примера рассчитаем фазы рассеяния частицы на прямоугольной яме:

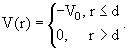(3.45)

В этом случае для получения волновой функции R_ℓ(r) во внутренней области не требуется численного интегрирования:

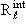(r) = const · jℓ(Kr) ,

(3.46)

где

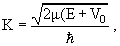(3.47)

Отсюда находим логарифмическую производную (3.43):

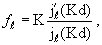(3.48)

а далее по формуле (3.44) и фазу рассеяния:

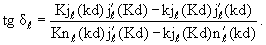(3.49)

В качестве другого примера рассмотрим рассеяние частицы абсолютно твердой сферой. На поверхности такой сферы (r = d) «внешняя» волновая функция обращается в нуль:

Подставляя сюда (3.41), находим

В частности, при малых энергиях частицы отсюда получаем

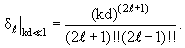(3.52)

б) Теория возмущений

    Если V(r) мало, то радиальную функцию R_ℓ(r), входящую в формулу (3.29) для фазы и удовлетворяющую уравнению (3.10), можно заменить во внутренней области (r < d) выражением
R_ℓ(r) → i^ℓ(2ℓ + 1)j_ℓ(kr). Тогда получаем приближенное выражение для фазы:

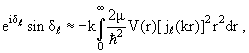(3.53)

а вместе с ним и для парциальной амплитуды рассеяния:

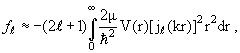(3.54)

    Согласно (3.54), амплитуда рассеяния ƒ(0) вещественна. С точки зрения оптической теоремы (3.28) такой результат, на первый взгляд, бессмыслен: мнимая часть амплитуды рассеяния вперед Im ƒ(0) равна нулю, а полное сечение σ, конечно, нет. Правда, если фазы рассеяния малы, то и мнимые части парциальных амплитуд Im ƒ_ℓ = (2ℓ + l)k^-1 sin² δ_ℓ, интегральные парциальные сечения
σ_ℓ = (4π/k²)(2ℓ + l) sin² δ_ℓ квадратичны относительно δ_ℓ; поэтому можно сказать, что при малых δ_ℓ, оптическая теорема выполняется приближённо − с точностью до членов, пропорциональных δ_ℓ².

Таким образом, условие применимости теории возмущений для фаз − это малость фаз:

Приближение (3.53) для фаз при соблюдении требования (3.55) будем называть борновским приближением для фаз рассеяния. Согласно (3.53) и (3.55), в этом приближении фазы вычисляются по формуле

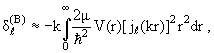(3.56)

Она показывает, в частности, что если V(r) везде отрицательно (потенциал притяжения), то все борновские фазы 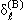положительны; формула (3.23) показывает, что в этом случае вся осцилляционная картина внешней волновой функции частицы как бы «подтягивается» в области взаимодействия. При положительном V(r) все борновские фазы отрицательны; волновая функция частицы в этом случае как бы «выталкивается» из области взаимодействия.
    Выясним условия, при которых соблюдается требование малости фаз (3.55). Как и в §2.2, рассмотрим два предельных случая: длина волны частицы 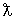= k^-1 много больше и много меньше, чем область взаимодействия.
    Если 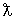>> d, т.е. kd << 1, то, подставляя в (3.56) аппроксимацию (3.30), получаем

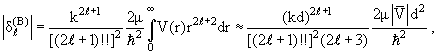(3.57)

где d − средний радиус области взаимодействия, a |V| − средняя амплитуда взаимодействия. Известно, что если сферически симметричный потенциал притяжения аппроксимируется прямоугольной ямой, то условие существования в нем связанного состояния − это

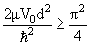(3.58)

Если же в потенциальной яме имеются два-три уровня, то параметр (2μ|V|d²)/ћ², которому пропорциональна величина |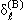| составляет несколько единиц. Формула (3.57) показывает, что условие применимости борновского приближения (3.55) может выполняться для фаз с большими ℓ и не выполняться для фаз с малыми ℓ. Хуже всего борновское приближение годится для фазы s-волны. С другой стороны, как видно из (3.25), относительный вклад s-волны в амплитуду рассеяния меньше всего при самых малых углах рассеяния. Отсюда следует важный качественный вывод: если энергия частицы и протяженность потенциала конечного радиуса таковы, что kd << 1, то при рассеянии на малые углы условия применимости борновского приближения всегда в среднем более благоприятны, чем при рассеянии на большие углы.
    Если 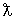<< d, т. е. kd << 1, то для оценки фаз рассеяния следует подставить в (3.56) аппроксимацию (3.12):

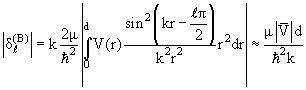(3.59)

В этом случае условие применимости борновского приближения

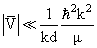(3.60)

не содержит ℓ и полностью совпадает с тем, что для случая kd >> 1 было получено в § 2.2.

в) Метод фазовых функций

    С точки зрения математики метод фазовых функций представляет собой особый способ решения радиального уравнения Шредингера (3.3), являющегося линейным дифференциальным уравнением второго порядка, или соответствующего ему интегрального уравнения (3.10). Он очень удобен для получения фаз рассеяния, так как по этому методу не требуется сначала вычислять в широкой области радиальные волновые функции задачи рассеяния и уже лишь потом, по их асимптотике, находить фазы. Сводя дело к решению нелинейного дифференциального уравнения первого порядка, метод фазовых функций очень удобен также с точки зрения выполнения численных расчетов на ЭВМ. Ниже мы изложим лишь основную идею этого метода.
    Будем отправляться от интегрального уравнения (3.10), куда подставим функции Грина (E,r,r') в форме (3.11). Тогда радиальную функцию R_ℓ(r) можно представить в виде

где c_ℓ(r) и s_ℓ(r) - две новые вспомогательные функции, определённые соотношениями

(3.62)

(3.63)

Используя (3.29), легко показать, что отношение этих функций при асимптотически больших г дает фазу рассеяния:

    Фазовой функцией называется функция δ_ℓ(r), определенная соотношением

Как видно из (3.64), ее предел при r → ∞ есть фаза рассеяния:

(3.66)

Легко убедиться путем непосредственной подстановки выражения (3.65), что фазовая функция δ_ℓ(r) удовлетворяет при всех r уравнению

(3.67)

которое надо решать с дополнительным условием:

Конечно, для получения предельного значения δ_ℓ(∞) достаточно интегрировать уравнение (3.67) от нуля до границы области взаимодействия. Это хорошо видно также, если уравнению (3.67) придать вид интегрального уравнения:

(3.69)

Уравнения (3.68) и (3.69) раскрывают физический смысл функции δ_ℓ(r): фазовая функция δ_ℓ(r), соответствующая заданному потенциалу V(r), − это фаза рассеяния частицы потенциалом, который «обрезан» в точке r, а на меньших расстояниях совпадает с V(r).

Упражнения

3.1. Найти связь между функцией Грина (Е,r,r') и функциями Грина (E,r,r'). 3.2. Получить общую формулу для фаз рассеяния δ_ℓ частицы потенциальной ямой глубины V₀ радиуса d с бесконечной отталкивающей серединой paдиуса а в центре ямы (см. рис.).

3.3. Вычислить борновскую фазу s-волны (k) при рассеянии частицы прямоугольной потенциальной ямой (3.45). Сравнить с точным решением (3.49). В случае kd << 1 выяснить, при каком соотношении параметров V₀ и d различие между точным и борновским значениями фазы δ₀ максимально; что означает такое соотношение?

3.4. С помощью уравнения (3.69) для фазовых функций получить формулу борновского приближения для фаз.

3.5. Пользуясь методом фазовых функций, показать, что если V(r) везде отрицательно (положительно), то не только борновская фаза δ_ℓ, но и точно значение фазы δ_ℓ положительны (отрицательны).

3.6. Используя соотношения (3.2) и (3.23), показать, что волновую функцию (r) можно записать в виде

(3.70)

где - вещественное решение уравнения (3.3) с асимптотикой

Показать, что тогда для волновой функции (r) справедливо выражение:

(3.71)