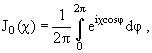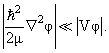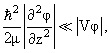Лекция 4. Рассеяние при низких и при высоких энергиях

§ 4.1. Рассеяние при низких энергиях. Длина рассеяния, обобщенная длина рассеяния, эффективный радиус взаимодействия

    Разложение по парциальным волнам является и удобным способом приближенного решения задачи рассеяния на сферически-симметричном потенциале, и способом параметризации экспериментальных данных о процессе рассеяния. Согласно соотношению (3.33), при малых энергиях частиц вклад высших парциальных волн в амплитуду рассеяния быстро падает с ростом ℓ. Если kd << 1, то достаточно знать лишь несколько первых фаз δ_ℓ, а в пределе k → 0 вообще лишь фазу s-волны δ₀, чтобы хорошо описать процесс рассеяния. На этом основан так называемый фазовый анализ рассеяния, который, будучи модельно независимым способом параметризации амплитуды рассеяния, широко применяется в разных областях физики. Как видно из (3.25), (3.26), характерным признаком процесса рассеяния в условиях kd << 1 («длинноволновое приближение») является малая (а в пределе k → 0 вообще исчезающая) угловая анизотропия рассеяния.
    Перейдем к описанию процесса рассеяния при предельно малых энергиях, когда достаточно ограничиться взаимодействием частицы с силовым центром в s-состоянии.
    Из (3.33) следует, что при Е → 0 фаза s-волны δ₀(k) пропорциональна импульсу частицы к. Соответствующий коэффициент пропорциональности является единственным параметром, через которые выражаются все характеристики процесса рассеяния при малых энергиях частицы. Определим длину рассеяния предельным соотношением

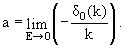(4.1)

Подставляя (4.1) в (3.25), а также учитывая, что при k → 0 все фазы δ_ℓ с ℓ ≠ 0 стремятся к нулю быстрее, чем δ₀, получаем

т.е. длина рассеяния есть амплитуда рассеяния (с обратным знаком) в пределе нулевой энергии частицы. При этом

    Что говорят величина и знак длины рассеяния о характере взаимодействия частицы с силовым центром? Для ответа на этот вопрос рассмотрим, каков с точки зрения профиля волновой функции «геометрический» смысл длины рассеяния. Во внешней области (r > d) волновая функция, описывающая s-рассеяние частиц, имеет, согласно (3.41), вид

при этом мы выразили сферическую функцию Бесселя и сферическую функцию Неймана через тригонометрические функции:

Распространим вьфажение (4.4) и на внутреннюю область:

При k → 0 и малых r функция v₀(r) − прямая линия:

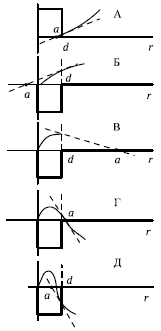
Рис. 4.1. Профиль волновой функции и длина рассеяния частицы.

Таким образом, значение длины рассеяния а − это координата точки, в которой пересекается с осью абсцисс касательная к функции v₀(r), если построить эту функцию при к → 0 (точнее при выполнении двух условий: кг << 1 и |ка| << 1). Геометрический смысл длины рассеяния виден из рис. 4.1. Здесь показаны три ситуации, возможные при сшивании внутренней и внешней волновых функций по «границе» области взаимодействия. Случай А относится к потенциалу отталкивания, случаи Б и В − к потенциалу притяжения; во всех случаях d − средний радиус взаимодействия.
    В случае А и В длина рассеяния а положительна. Однако в случае
А (0 < а < d) волновая функция u(r) «выталкивается» из внутренней области (отталкивание частицы силовым центром), а в случае В (а > d) она «втягивается» в неё (притяжение). Добавим, что в случае А волновая функция u₀(r) ведёт себя во всей внешней области г > d так же, как при рассеянии частицы абсолютно твердой (отталкивающей) сферой, радиус которой равен а.
    В случае Б длина рассеяния а отрицательна (фаза положительна). Из рисунка видно, что в этом случае волновая функция также «втягивается» в область взаимодействия, но значительно слабее, чем в случае В: поведение функций u₀(r) и функции v₀(r) во внутренней области не так сильно различается между собой в случае Б, как в случае В. Переход от одной ситуации к другой легко понять, предположив, что, отправляясь от случая Б мы постепенно увеличиваем амплитуду взаимодействия частицы с силовым центром. При этом будет возрастать скорость осцилляции волновой функции u₀(r) во внутренней области, и при каком-то значении амплитуды взаимодействия, где-то в районе r = d возникнет максимум функции u₀(r), так что наклон функции
v₀(r) изменится на противоположный (длина рассеяния а изменит знак): мы перешли к случаю В. Нетрудно предположить, что такой переход должен быть сопряжен с качественным изменением и каких-то других свойств системы.
    Действительно, при переходе от ситуации Б к ситуации В в яме возникает связанное состояние частицы. Рассмотрим случай, когда энергия связи ε_b такого только что возникшего связанного состояния еще очень мала:

здесь V − средняя глубина взаимодействия. Пусть u_b(r) = rR_b(r) − волновая функция этого состояния. Её поведение во внешней области не зависит от характера потенциала:

где κ = (2με_b)^1/2/ћ. Сравним волновую функцию u_b(r) с волновой функцией u₀(r), описывающей процесс рассеяния на том же потенциале при очень малых энергиях. Очевидно, что форма этих двух функций во внутренней области (r < d) при ε_b → 0 и k → 0 одна и та же. А это значит, что и логарифмические производные этих двух функций на границе внутренней и внешней областей также совпадают:

Подставляя сюда u₀(r) из (4.4), a u_b(r) из (4.9), получаем при к → 0

или в соответствии с (4.1)

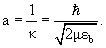(4.12)

Итак, если в потенциальной яме имеется слабо связанное s-состояние, длина рассеяния частицы такой ямы положительна, а её величина а полностью определяется энергией связи частицы.
    Приведенные выше рассуждения относительно перехода от ситуации Б к ситуации В, изображенных на рис. 4.1, полезно продолжить. Проследим за изменением профиля волновой функции u₀(r) при дальнейшем увеличении амплитуды взаимодействия (глубина ямы). Переход от случая В к случаю Г сопровождается непрерывным уменьшением длины рассеяния. Далее (случай Д) длина рассеяния попадает в интервал 0 < а < d. Это происходит одновременно с тем, как нуль функции u₀(r), который в случае Б −Г находится где-то справа от d, перемещается во внутреннюю область. При дальнейшем увеличении глубины ямы длина рассеяния проходит через нуль, и возникает ситуация, сходная со случаем Б.
    Таким образом, по мере непрерывного увеличения глубины ямы происходит циклическое изменение параметра сшивания внутренней и внешней волновых функций задачи рассеяния, а вместе с ними − и величины и знака длины рассеяния. Завершению каждого «цикла» сопутствует появлению в яме нового связанного состояния.
    Рассмотренные выше случаи Б, В, Г, Д относились к потенциалу притяжения, а случай А − к потенциалу отталкивания. Заметим, однако, что поведение функции v₀(r) во внешней области в случае Д сходно с тем, что происходит в случае А (изменение знака всей функции, конечно, несущественно). Другими словами, если в яме притяжения существует связанное состояние, то может случиться, что при к → 0 s-волна искажается (во внешней области) этой ямой так же, как потенциалом отталкивания.

Пример: s-рассеяние на прямоугольной яме.

    Задача s-рассеяния на прямоугольной яме − одна из немногих, когда без численных расчетов удается получить точные результаты для фазы и всех других характеристик рассеяния. Мы воспользуемся этим случаем, чтобы проиллюстрировать общие выводы, сделанные выше.
    Пусть V₀ − глубина, a d − радиус прямоугольной ямы. Число связанных s-состояний N_s в такой яме определяется неравенством [1, с. 121]

где

Таким образом, первое связанное состояние появляется при k₀d > π/2, n-е − при k₀d > (n − 1/2)π.
    Фазу s-волны при рассеянной частице такой ямы легко получить из (3.49):

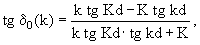(4.15)

где, согласно (3.47), K = (2μ(V₀ + E)/ћ²)^1/2. Отсюда получаем для длины рассеяния

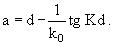(4.16)

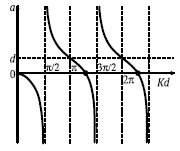
Рис. 4.2. Длина рассеяния частицы прямоугольной ямой в зависимости от параметров ямы.

    На рис. 4.2 видны диапазоны изменения длины рассеяния а в разных интервалах величины Kd. Решая трансцендентное уравнение
х − tg х = 0, получаем, что длина рассеяния обращается в нуль в точках Kd = 0, 4.49, 7.76 и т.д. Слева от каждой из них на рисунке обозначены интервалы величины Kd, где а заключено в пределах 0 < а < d; здесь внешняя волновая функция такая же, как при рассеянии на бесконечном отталкивающем потенциале. В точках Kr = π/2, 3π/2, 5π/2 и т.д. длина рассеяния меняется скачком от а = −∞ до а = +∞. Из (4.13) видно, что как раз при переходе величины Kr, через эти точки в яме возникают новые связанные состояния.
    До сих пор мы интересовались лишь рассеянием в пределе k → 0, а формулой (4.15), справедливой при любом k, воспользовались лишь как вспомогательной. Теперь обратимся к описанию s-рассеяния при ненулевых, хотя и малых, энергиях.
    Введём понятие обобщённой длины рассеяния:

Очевидно, в пределе k → 0 обобщённая длина рассеяния a(k) превращается в длину рассеяния а. Представим правую часть выражения (4.17) в виде разложения по степеням k. Из соотношений (3.10) и (3.29) видно, что 1/a(k) − это четная функция k, поэтому ее разложение содержит только четные степени k. При малых k проходит следующая параметризация обобщённой длины рассеяния:

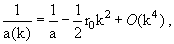(4.18)

где 0(k⁴) − член разложения высшего порядка, который мы отбросим. Параметр r₀ носит название эффективного радиуса потенциала взаимодействия.
    Таким образом, длина рассеяния а и эффективный радиус r₀ являются двумя независимыми параметрами, через которые можно выразить фазу s-волны во всей области малых энергий частицы. Это утверждение справедливо для потенциала конечного радиуса, имеющего произвольную форму. Отсюда следует, в частности, что если изучать экспериментально рассеяние частицы потенциалом лишь при малых энергиях − в области применимости разложения (4.18), то нельзя получить более детальную информацию о форме потенциала, чем ее может дать простейшая модель прямоугольной ямы.

§ 4.2. Рассеяние при высоких энергиях. Эйкональное приближение.

    Перейдем к описанию потенциального рассеяния в противоположном случае высоких энергий налетающих частиц. Пусть дебройлевская длина волны частицы будет много меньше, чем размеры области взаимодействия:

<< d;  kd >> l .

(4.19)

В этом случае параметризация амплитуды рассеяния с помощью фаз, конечно, не подходит, так как в процессе рассеяния участвует очень большое число парциальных волн. Однако и борновское приближение, общие условия применимости которого выражаются неравенством (2.13), также не всегда годится. В этой ситуации нужны особые приближенные методы. Мы увидим, что рассеяние частиц потенциалом в условиях очень малой длины волны частицы обнаруживает большое сходство с дифракцией плоской волны, как она рассматривается в оптике. Вместе с этим в квантовую теорию рассеяния естественным образом проникают термины, присущие классической механике, − прицельный параметр, траектория движения частицы. На этой основе и удается сформулировать очень эффективный приближенный метод, который имеет много разных названий − дифракционное приближение, эйкональное приближение, приближение Мольера и др. − и широко применяется в разных разделах физики − от атомной физики до физики элементарных частиц.
    Рассмотрим рассеяние частиц потенциалом конечного радиуса V(г); при этом, в отличие от § 4.1, не требуется, чтобы этот потенциал был сферически-симметричным.
    В эйкональном приближении решение уравнения Шредингера ищется в виде

где φ(r) − функция, удовлетворяющая граничному условию:

Подставляя (4.20) в уравнение. Шредингера (1.4), получаем уравнение для функции φ(r):

(4.22)

Далее, функция φ(r) считается столь медленно изменяющейся, что вкладом вторых производных можно пренебречь. Тогда уравнение (4.22) принимает вид:

(4.23)

Интегрируя это уравнение с учетом граничного условия (4.21), находим

(4.24)

Согласно (1.34), амплитуда рассеяния на потенциале V(r) есть

(4.25)

где (r) − решение уравнения Шредингера, соответствующее импульсу падающих частиц к. В эйкональном приближении, согласно (4.20) и (4.24)

(4.26)

где введен единичный вектор в направлении импульса падающих частиц:

= k/k

(4.27)

и проекция b вектора r на плоскость, перпендикулярную вектору k:

r = b + z .

(4.28)

Подставляя (4.26) в (4.25), получаем:

(4.29)

где, как обычно,

θ - угол рассеяния. Используя (4.28) и (4.30), находим:

а при малых углах рассеяния, когда вектор q практически перпендикулярен вектору k, получаем

Подставляя (4.32) в (4.29) и записывая элемент объема в виде:

где d²b − элемент площади в плоскости, перпендикулярной вектору k, интегрируем по z:

(4.34)

(4.35)

    Полученная формула для амплитуды рассеяния аналогична формуле для амплитуды, описывающей в оптике дифракцию Фраунгофера. Пользуясь этой оптической аналогией, можно назвать функцию
χ(b) эйконалом, а выражение (4.34) эйкональным приближением для амплитуды рассеяния. Из формулы (4.35) видно, что функция χ(b) есть интеграл от потенциала по прямой, параллельной вектору k и проходящей на расстоянии |b| от начала координат. Поэтому величину b можно назвать вектором прицельного параметра этой прямолинейной траектории. Тогда амплитуду (4.34) можно рассматривать как интеграл по множеству таких прямолинейных траекторий со всевозможными значениями прицельного параметра.

Функция

однозначно определяемая эйконалом χ(b) и связанная двумерным преобразованием Фурье с эйкональной амплитудой рассеяния:

(4.37)

называется профильной функцией взаимодействия. Она играет важную роль в теории дифракционного рассеяния частиц на составных системах (см. лекцию 15).
    Если потенциал V(r) является азимутально-симметричным, т.е. не зависит от направления вектора b, то выражение (4.34) для амплитуды можно упростить. При малых углах рассеяния, когда вектор q лежит в плоскости, перпендикулярной k, можем записать qb = qb cos φ, где φ − азимутальный угол вектора b, отсчитываемый относительно направления вектора q. При этом d₂b = b  db  dφ. Используя интегральное представление цилиндрической функции Бесселя:

(4.38)

получаем из (4.34) в случае азимутально-симметричного потенциала

(4.39)

Эта амплитуда не зависит от направления переданного импульса q. Амплитуда рассеяния в эйкональном приближении существенно отлична от нуля только для малых углов рассеяния. Из (4.35) видно, что χ(b) обращается в нуль при b ≥ d. Поэтому существенной областью интегрирования в (4.34) является 0 ≤ b ≤ d. Считая, что exp (iχ(b)) плавно изменяется во внутренней области, видим, что ввиду осцилляции экспоненты exp (iqb) амплитуда (4.34) существенно отлична от нуля только в том случае, если

Подставляя сюда (4.30) и учитывая (4.19), получаем, что это условие можно записать в виде

Таким образом, согласно эйкональному приближению, при высоких энергиях рассеяние сосредоточено в узком конусе, ось которого совпадает с направлением импульса бомбардирующих частиц, а угол раствора характеризуется величиной l/(kd).

§ 4.3. Сравнение эйконального и борновского приближений. Условия применимости эйконального приближения

    В § 3.4 мы отмечали, что амплитуда рассеяния в борновском приближении не удовлетворяет оптической теореме: действительно, при θ = 0 она всегда вещественна. Получим
ƒ^(B)(0) = −[μ/(2πћ²)] / ∫V(r)d³r, тогда как, согласно (3.28), мнимая часть амплитуды рассеяния вперед может обращаться в нуль только вместе с полным сечением взаимодействия, что практически невозможно. Покажем, что амплитуда рассеяния, рассчитанная в эйкональном приближении, лишена такого дефекта. Для этого, пользуясь выражением (4.34), рассчитаем в эйкональном приближении полное сечение σ. Переходя, по аналогии с (2.22), от интегрирования по направлениям, рассеяния к интегрированию по переданному импульсу:

и используя интегральное представление δ-функции от двух переменных:

Получаем:

здесь мы учли также, что при любом вещественном V(r) эйконал χ(b) является вещественной величиной. С другой стороны, для мнимой части амплитуды рассеяния вперед имеем

    Сравнивая два последних выражения между собой, видим, что они удовлетворяют оптической теореме (3.28). Это является свидетельством внутренней последовательности, самосогласованности эйконального приближения в теории потенциального рассеяния.
    Чтобы выяснить условия применимости эйконального приближения, вернемся к соотношениям (4.22), (4.23), от которых мы отправлялись при получении выражения (4.34). Переход от первого из них ко второму возможен, если во всей области взаимодействия r < d справедливо неравенство

(4.42)

Тогда φ(r) имеет вид (4.24). Рассмотрим вместо (4.42) другое неравенство

(4.43)

считая, что требование (4.42) предъявляется к V(r) и φ(r), так сказать, в среднем, и включает в себя (4.43). Подставляя dφ/dz из (4.23), получаем

(4.44)

или, если снова использовать (4.23)

(4.45)

что ведет к двум неравенствам, которые должны выполняться одновременно (опять-таки, по крайней мере, в среднем):

(4.46)

(4.47)

Первое из них (если ограничиться потенциалами, не имеющими резких спадов и подъемов) эквивалентно требованию 1/d << k, которое в формуле (4.19) уже было нами использовано при разработке эйконального приближения. Второе означает, что средний потенциал взаимодействия |V| должен быть много меньше кинетической энергии налетающих частиц Е. Вспомним также, что при переходе от (4.24) к (4.34) мы сделали еще предположение о малости углов рассеяния.
    Таким образом, условия применимости эйконального приближения формулируются в виде трех требований:

Отметим, имея в виду большую величину kd, что последнее из этих требований гораздо менее жестко, чем условие применимости борновского приближения (2.13): |V| << Е/(kd). Если же выполняется не только условие (4.48), но и условие (2.13), то выражение (4.34) для амплитуды рассеяния, полученное в эйкональном приближении, переходит в борновскую амплитуду рассеяния (2.6) (см. упр. 4.3).

Упражнения:

4.1. Вычислить длину рассеяния частицы прямоугольной потенциальной ямой с бесконечной отталкивающей сердцевиной в центре ямы.

4.2. Вычислить эффективный радиус r₀ прямоугольной потенциальной ямы. Сравнить зависимость r₀ от глубины и радиуса ямы с зависимостью длины рассеяния а от этих параметров.

4.3. Показать, что при условии |V| << Е/(kd) эйкональная амплитуда рассеяния (4.34) переходит в борновскую амплитуду (2.6).

4.4. При высоких энергиях амплитуда упругого рассеяния адронов нуклонами часто аппроксимируется выражением

(4.49)

где σ, β и α − параметры, не зависящие от переданного импульса q. Вычислить профильную функцию адрон-нуклонного взаимодействия Г(b).

4.5. Вычислить эйконал и профильную функцию для частицы, рассеиваемой прямоугольной сферически-симметричной ямой.