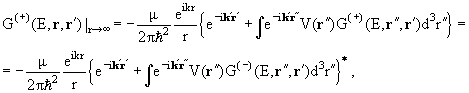Лекция 6. Дополнительные вопросы теории потенциального рассеяния

§ 6.1. Функция Грина частицы, движущейся в поле силового центра

    В § 1.1−1.2 мы ввели функцию Грина (гриновский оператор) свободного движения частицы:

(6.1)

где − оператор кинетической энергии частицы. Введем по аналогии с (6.1) функцию Грина, описывающую движение частицы в заданном потенциальном поле V(г):

(6.2)

где = ₀ + V(r). Из эрмитовости гамильтониана следует соотношение

(+)(E) = [(−)(E)]+ .

(6.3)

    Выясним связь между операторами (6.1) и (6.2). Для этого воспользуемся операторным тождеством

(6.4)

Полагая = (E^(±) − ), а = (E^(±) − ₀), получаем

(±)(E) = (E) + (E)(±)(E).

(6.5)

Это соотношение можно рассматривать как операторное уравнение для функции Грина G^(±)(E). В координатном представлении оно имеет вид

<r' |(±)(E)| r> = <r' |(E)| r> + ∫ <r' |(E)| r">V(r")<r" |(E)| r>d3r".

(6.6)

где матричные элементы:

<r' |^(±)(E)| r> ≡ (E,r,r').

даются формулами (1.21), (1.22).
    Запишем соотношение (6.5) более компактно:

(±)(E) = (E)[1 + (±)(E)].

(6.7)

Заметим, что оно справедливо для операторов (6.1) и (6.2), определенных для любого комплексного параметра Z:

(6.8)

Наряду с (6.5) легко получить и обратное соотношение. При произвольном Z они имеют вид

(Z) = 0(Z)[1 + (Z)],

(6.9)

0(Z) = (Z)[1 − 0(Z)].

(6.10)

    С помощью функции Грина G^(±)(Z) иногда оказывается удобным переформулировать основное уравнение стационарной теории потенциального рассеяния − уравнение Липпмана − Швингера (1.32). Запишем его сначала в компактной форме:

= φk+ (E) ,

(6.11)

где первый член в правой части − это по-прежнему плоская волна:

Подставим (6.10) в (6.11):

= φk+ (±)(E)[1 − ] ,

(6.13)

Комбинация [1 − ], как видно из (6.11), есть φ_k. Таким образом, можно исключить из правой части формулы (6.13) функцию :

= φk+ (±)(E)φk.

(6.14)

В координатном представлении это же соотношение имеет вид

= eikr + ∫ G(±)(E,r,r' )V(r' ) eikr' d3r' .

(6.15)

    В различных задачах многоканальной теории столкновений необходимо знать асимптотику функции Грина частицы, движущейся в заданном потенциальном поле. Рассмотрим этот вопрос.
    Запишем в координатном представлении соотношение (6.7):

и поставим сюда асимптотическое выражение функции Грина свободной частицы (1.23). Тогда получаем

(6.17)

где звездочка означает комплексное сопряжение.
    Воспользуемся теперь соотношением (6.3). В координатном представлении оно имеет вид

< r |(+)(E)| r' > = < r |(−)(E)| r' >* ,

(6.18)

т.е.

G(+)(E,r,r' ) = [(−)(E,r,r' )]*

(6.19)

Подставляя (6.19) в (6.17), получаем

В фигурных скобках мы узнаём правую часть выражения (6.15). Таким образом, окончательно асимптотическое выражение функции Грина для частицы, движущейся в заданном потенциале, принимает вид

(6.20)

Напомним, что модуль вектора к' определяется энергией частицы Е, а направлен он по вектору г:

§ 6.2. Оператор перехода (-оператор)

    Во многих задачах теории столкновений (особенно при рассмотрении многочастичных систем) очень удобным оказывается использование так называемого -оператора (оператора перехода). Определим его сначала для случая потенциального рассеяния и рассмотрим на этом примере его свойства.
    В качестве такого определения можно взять одно из следующих соотношений:

(Z) = + (Z),

(6.22)

(Z) = + 0(Z)(Z),

(6.23)

которые легко перевести друг в друга, если воспользоваться соотношениями (6.9), (6.10), связывающими между собой гриновские операторы ₀(Z) и (Z).
    Подействуем оператором (6.23) на волновую функцию свободного движения (6.12):

(Z)φk = φk + 0(Z)(Z)φk.

(6.24)

Одновременно подействуем на левую и правую части уравнения Липпмана − Швингера (6.11) оператором V:

= φk + (E) .

(6.25)

Сравнивая (6.25) с (6.24), находим соотношение

(6.26)

    Обратимся к общему выражению амплитуды потенциального рассеяния (1.34):

(6.27)

Входящие в интеграл функции φ_k' = е^ik'r и (r) относятся к разным гамильтонианам: первая − к гамильтониану свободного движения ₀, а вторая − к гамильтониану частицы в потенциальном поле = ₀ + . Поэтому общее выражение (6.27) нельзя рассматривать как матричный элемент какого-либо оператора между состояниями одного и того же набора. Если, однако, подставить в (6.27) соотношение (6.26), то мы как раз получаем такую возможность:

(6.28)

Отсюда виден смысл термина оператор перехода: матричный элемент -оператора есть амплитуда перехода из состояния свободного движения с импульсом k в состояние свободного движения с импульсом k'.
    Для нахождения -оператора удобно пользоваться импульсным представлением. В связи с этим уточним еще раз наши обозначения. Закрепим дираковские обозначения |k> за векторами состояний свободного движения, образующими полный ортонормированный набор:

< k | k' > = δ(k − k' ).

(6.29)

Такой выбор означает, что в х-представлении волновая функция свободного движения, есть

(6.30)

где φ_k = е^ikr по-прежнему соответствует формулам (1.6) и (6.12). Таким образом, в дираковских обозначениях амплитуда рассеяния (6.28) есть следующий матричный элемент:

(6.31)

где E − энергия частицы, величина которой однозначно определена импульсами k и k':

в нерелятивистском случае

Совокупность матричных элементов -оператора в обкладках состояний свободного движения частицы <k' |(Z)| k> называется t-матрицей. Будем говорить, что мы рассматриваем -оператор (Z) на массовой поверхности (или, как более принято в нерелятивистской теории, − на энергетической поверхности) если параметр Z = Е в матричных элементах <k' |(E)| k> связан с импульсами k и k' соотношением (6.32).
    Необходимость рассмотрения -оператора вне массовой поверхности видна сразу же, как только мы приступим к решению уравнений для этого оператора. Запишем, например, уравнение (6.23) в импульсном представлении:

(6.34)

    Гриновский оператор ₀(Z) в этом представлении диагоналей:

(6.35)

Поэтому для (6.34) имеем

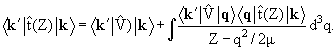(6.35)

Входящий под интеграл элемент t-матрицы <q |(Z)| k> представляет -оператор вне массовой поверхности, так как импульс q и параметр Z не связаны между собой никаким соотношением, даже если матричный элемент в левой части равенства соответствует условию (6.32).
    Уравнение (6.36) для -оператора эквивалентно уравнению (1.32) для ψ-функции. Будем также называть его уравнением Липпмана − Швингера. Часто бывает удобно изобразить его графически:

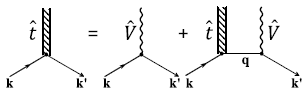(6.37)

где тонкая волнистая линия изображает однократное взаимодействие частицы с силовым центром, а широкая линия − суммарный эффект взаимодействий всех кратностей; q − импульс свободно движущейся частицы в промежуточном состоянии.

§ 6.3. Решение уравнения Липпмана − Швингера для -оператора. Случай сепарабельного взаимодействия

    Общих методов решения уравнения (6.36), (6.37), которые были бы пригодны для любого взаимодействия , не существует. Если взаимодействие мало, можно воспользоваться методом итераций. Видно, в частности, что графическое уравнение (6.37) превращается в этом случае в ряд диаграмм (2.3). В низшем порядке теории возмущений t-матрица совпадает с матрицей потенциала взаимодействия :

<k' |(Z)| k>(B) = <k' || k>

(6.38)

и, следовательно, не зависит от Z
    Другой случай, когда уравнение Липпмана - Швингера имеет простое (и точное!) решение − это случай сепарабельного взаимодействия .
    Пусть в матрице <k' |)| k> переменные k и k' разделяются:

<k' |)| k> = -λg(k)g(k' ),

(6.39)

здесь λ − вещественная константа, характеризующая силу взаимодействия. Потенциалы типа (6.39) эффективно используются в ядерной физике. Таков, например, один из широко известных сепарабельных потенциалов − потенциал Ямагучи, где формфактор g(k) выбирается в виде

    Подставим (6.39) в уравнение Липпмана − Швингера (6.36) и будем искать t-матрицу в виде

<k' |(Z))| k> = Λ(Z)g(k)g(k' ).

(6.41)

Тогда для искомой функции Λ(Z) получаем алгебраическое уравнение

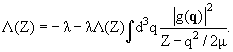(6.42)

с простым решением:

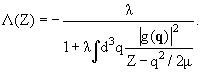(6.43)

Чтобы найти амплитуду рассеяния частицы на потенциале (6.39), функцию Λ(Z) надо вычислить в точке Z = E⁽⁺⁾ с соответствующим обходом полюса при интегрировании по q. В отличие от борновской амплитуды, которая при θ = 0 вещественна и потому не удовлетворяет оптической теореме, амплитуда (6.41) при k' = k, вообще говоря, комплексна. Используя оптическую теорему, можно найти полное сечение рассеяния частицы на потенциале (6.39).

§ 6.4. Об аналитических свойствах t-матрицы

    Воспользуемся полученным выше точным решением задачи потенциального рассеяния и рассмотрим на его примере вопрос об аналитических свойствах t-матрицы.
    Согласно соотношению (6.43), функция Λ(Z), a следовательно, и t-матрица <k' |(Z))| k> имеют полюс в точке Z = Z₀, где обращается в нуль знаменатель всего выражения (6.43); значение Z₀ удовлетворяет алгебраическому уравнению

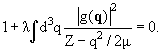(6.44)

    Дальше мы увидим, что при λ < 0 (потенциал отталкивания) это уравнение не имеет решений на вещественной оси Z; если же λ > 0 (потенциал притяжения), то такие решения могут быть при
Z₀ < 0. Отрицательные значения энергии частицы соответствуют ее связанным состояниям. В связи с этим обратимся к задаче о связанных состояниях частицы в сепарабельном потенциале (6.39).
    В р−представлении стационарное уравнение Шредингера для волновой функции связанного состояния φ₀(k) имеет вид

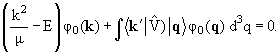(6.45)

Подставляя сюда (6.39), находим φ₀(k) с точностью до нормировочного множителя:

(6.46)

Чтобы найти собственные значения Е, перепишем (6.46) в форме, непосредственно следующей из (6.45):

(6.47)

затем умножим правую и левую части на g(k) и проинтегрируем по d³k. Отсюда получаем

(6.48)

Это есть не что иное, как уравнение (6.44) для нахождения полюсов t-матрицы. Таким образом, вещественные полюса t-матрицы <k' |(Z)| k> лежат на отрицательной полуоси и совпадают с энергиями связанных состояний частицы. Это свойство t-матрицы, установленное нами на примере движения частицы в сепарабельной потенциале, является в действительности общим свойством
t-матрицы любых простых и сложных систем.

§ 6.5. Эйкональное приближение для функции Грина свободной частицы

    Здесь мы рассмотрим, еще один дополнительный вопрос теории потенциального рассеяния, который не связан с материалом предыдущих параграфов данной лекции, но имеет значение для дальнейшего. Обратимся к уравнению (4.23):

(6.49)

которое вместе с дополнительным условием

дает решение задачи потенциального рассеяния в эикональном приближении:

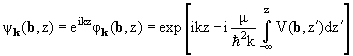(6.51)

(здесь, как и в § 4.2, ось z выбрана вдоль импульса падающих частиц k). Заметим, что дифференциальное уравнение первого порядка (6.49) вместе с дополнительным условием (6.50) эквивалентно следующему интегральному уравнению:

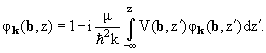(6.52)

Перепишем это уравнение для самой волновой функции:

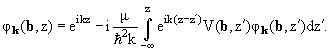(6.53)

Ему можно придать форму уравнения Липпмана − Швингера (1.13), если функцию Грина свободной частицы записать в виде

(6.54)

где θ(x) − ступенчатая функция

(6.55)

а r = {b,z}, r' = {b',z'} − цилиндрические координаты частицы.
    Мы будем называть выражение (6.54) эйкональным приближением для функции Грина свободной частицы. Заметим, что уравнение (6.49), от которого мы отталкивались, справедливо лишь в области действия силового центра и не годится для рассмотрения асимптотических свойств волновой функции частицы. То же самое относится и к выражению (6.54); оно годится, лишь когда обе точки r и r' лежат в области действия потенциала V(r).

Упражнения

6.1. Для сепарабельного потенциала Ямагучи (6.40), заданного в р−представлении, найти потенциал <r' || r> в х −представлении.

6.2. Найти длину рассеяния частицы на потенциале Ямагучи.

6.3. Вычислить полное сечение рассеяния частицы на потенциале Ямагучи (6.40).

6.4. t-Матрица (6.41), описывающая взаимодействие частицы с силовым центром, задана в виде

<k' || k> = b·(k k' ),

(6.56)

где b − некоторая константа. Найти угловое распределение рассеянных частиц. Показать, что в
х−представлении t-матрица (6.56) имеет вид

<r' || r> = (2π)3b·[rδ(r)][r'δ(r')].

(6.57)

6.5. Для потенциала Ямагучи записать волновую функцию связанного состояния φ₀(k) в
х−представлении. Выяснить поведение волновой функции φ₀(r) при r → ∞.