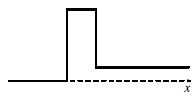
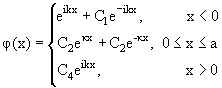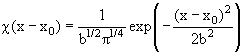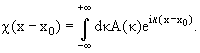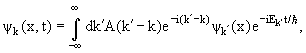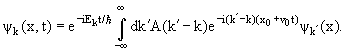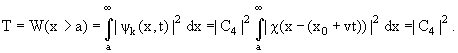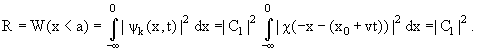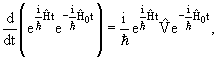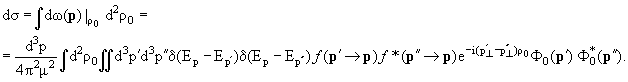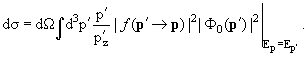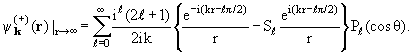Лекция 7. Нестационарная теория столкновений
§ 7.1. Столкновения при одномерном движении
Изложенная в предыдущих лекциях формулировка квантовой
задачи столкновений существенно опирается на интуитивные соображения и, как мы
видели в § 1.3, содержит внутренние противоречия. Присущее стационарной теории
представление о том, что плоская волна описывает бесконечный стационарный поток
падающих частиц, не укладывается в рамки постулатов квантовой механики, согласно
которым лишь квадратично-интегрируемые волновые функции могут описывать реальные
состояния физических систем. То же относится и к искаженным волнам
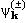 (r). (r).
В данной лекции мы увидим, что методы расчета столкновений,
разработанные в рамках стационарной теории, можно строго обосновать, если
сформулировать задачу столкновений как нестационарную задачу. При таком подходе,
рассматривая движение частиц как распространение волнового пакета, можно
независимо получить общие формулы теории столкновений (1.41) и (1.34), из
которых, как мы видели, следуют разнообразные частные − как точные, так и
приближенные результаты.
Мы начнем с более простой задачи, чем та, что рассматривалась
в лекции 1, − о столкновениях при одномерном движении.
Пусть поток частиц с массой μ и импульсом k движется вдоль
оси х и встречает на своем пути прямоугольный барьер. Найдем вероятность
прохождения частиц через барьер − коэффициент прохождения Т(k) или коэффициент
отражения R(k) = 1 − Т(k). Часто эта задача благодаря математической легкости ее
решения в рамках стационарной теории считается одной из простейших задач
квантовой механики. Действительно, если описать падающие на барьер частицы
плоской волной φ0(x) = eikx, то решением стационарного
уравнения Шредингера для рассматриваемой задачи будет волновая функция:
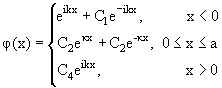 |
(7.1) |
где k и κ связаны с кинетической энергией падающих частиц Е и высокой барьера
V0:
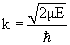 ; ; |
(7.2) |
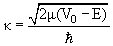 ; ; |
(7.3) |
(для определенности мы записали (7.1) применительно к случаю Е < V0).
Коэффициент С1 определяет интенсивность отраженной, а коэффициент С4
− прошедшей волны:
|
R = |С1|2; T = |С4|2 |
(7.4) |
Значения коэффициентов Cl, ... , C4
найдем из условий сшивания волновой функции и ее производной в точках разрыва
потенциала при х = 0 и х = а; они как раз дают необходимое число уравнений для
нахождения этих коэффициентов. Опустим простые выкладки и приведем окончательный
результат:
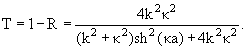 |
(7.5) |
Хорошо видно сходство приведенного хода рассмотрения с тем,
как мы решали в § 1.1 − 1.3 задачу потенциального рассеяния в трехмерном случае.
Теперь пойдем другим путем и получим тот же результат (7.4), (7.5) с помощью
нестационарной теории столкновений.
|
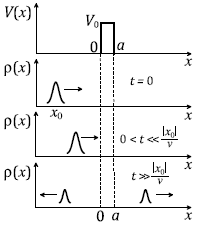
Рис. 7.1. Прямоугольный потенциальный барьер. Начальный
волновой пакет. Распределение координаты частицы для
различных моментов времени. |
Зададим состояние нашей частицы в начальный
момент времени t = 0 волновым пакетом:
|
ψ(x, t = 0) = Ф(х) = eikx χ(x − x0) , |
(7.6) |
где χ(ξ) − некоторая симметричная «колоколообразная» функция, имеющая
максимум при ξ = 0. Легко проверить, что такой пакет описывает частицу,
локализованную в окрестности точки х = х0 и движущуюся со средней
скоростью v = ћk/μ. Пусть х0 < 0, а k > 0. Тогда, согласно рис. 7.1,
мы имеем пакет, движущийся слева в сторону барьера.
Сначала, пока основной массив пакета не достиг барьера (частица
движется свободно) соответствующий интервал времени характеризуется величиной
порядка t0 = |x0|/v. Известно, что при свободном движении
пакет с течением времени расплывается тем быстрее, чем больше неопределенность
его импульса (т.е. чем меньше неопределенность координаты) [1, § 16]. Так, в
случае пакета гауссовой формы:
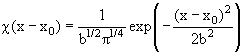 |
(7.7) |
начальная дисперсия координат Dx(t = 0) = b2/2
удваивается за время
В дальнейшем будем предполагать, что дисперсия пространственного
распределения частицы в состоянии (7.6) столь велика, что можно пренебречь
расплыванием пакета за время движения t0. В частном случае пакета
гауссовой формы это означает:
То же неравенство полезно переписать для дисперсии
импульса частицы:
|
Dp = (1/2)b2 << k/(2х0) |
(7.10) |
(в отличие от дисперсии координаты она при свободном движении частицы не
меняется). Далее нам будет удобно представить функцию χ(x − x0) в
виде интеграла Фурье:
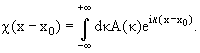 |
(7.11) |
Очевидно, что колоколообразной форме функции χ(ξ) соответствует сходная с ней
колоколообразная форма функции A(κ). Будем считать, что начальные
пространственные размеры пакета много меньше, чем расстояние х0 от «центра
тяжести» пакета до барьера при t = 0. Вместе с (7.9) это условие соответствует
тому, что ширина распределения А(κ) значительно меньше среднего импульса частицы
k.
Задача о рассеянии частицы на потенциальном барьере сводится
к решению нестационарного уравнения Шредингера:
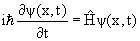 |
(7.12) |
с начальным условием (7.6). Как известно, общее решение уравнения (7.12)
можно выразить через решения соответствующего стационарного уравнения
 ψk(x)
= Ekψk(x). ψk(x)
= Ekψk(x). |
(7.13) |
Покажем, что нужное нам решение, удовлетворяющее начальному условию (7.6),
имеет вид
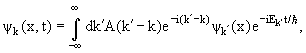 |
(7.14) |
где ψk' (x) − не что иное, как уже известное нам решение
(7.1) стационарного уравнения Шредингера (7.13).
Выше мы предположили, что ширина распределения А(k' −
k) значительно меньше, чем k. Поэтому в подынтегральном выражении (7.14) можно
заменить Ек' приближенным значением:
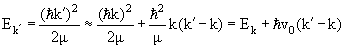 |
(7.15) |
и, следовательно, упростить выражение (7.14):
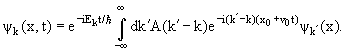 |
(7.16) |
Подставим сюда выражение (7.1) для функции ψk'
(x), имея в виду, что коэффициенты С1, С2, С3,
С4 уже найдены из условий сшивания. Тогда в областях − слева и справа
от барьера получаем
ψk (x,t)|x<0 = eikx e-iEt/ћ
χ(x − (x0 + vt)) + +C1e-ikx e-iEt/ћ
χ(−x − (x0 + vt));
ψk (x,t)|x>a = C4eikx
e-iEt/ћ χ(x − (x0 + vt)). |
(7.17) |
В частности, при t = 0
ψk (x,t = 0)|x<0 = eikx χ(x
− x0) + +C1e-ikx χ(−x − x0);
ψk (x,t = 0)|x>a = C4eikx
χ(x − x0). |
(7.18) |
Теперь вспомним, что, по условию, «ширина» распределения
χ(ξ) много меньше, чем х0. Значит, при t = 0 в область х < 0 попадает
лишь «хвост» функции х(−х − х0), равно как в область х > 0 − лишь «хвост»
функции χ(x − x0). Пренебрегая ими, видим, что с учетом специфических
свойств, функции
χ(ξ) выражение (7.18) эквивалентно условию (7.6) во всей области −∞ < х < ∞.
Итак, мы показали, что волновая функция ψk(x,t),
даваемая выражением (7.14), удовлетворяет и нестационарному уравнению Шредингера
(7.12), и начальному условию (7.6), т.е. является искомым решением
рассматриваемой задачи. Разберем физический смысл этого решения. Для этого
удобно снова обратиться к выражению (7.17). В области х < 0 при t < |x0|/v
существен только первый член, описывающий движение частицы слева направо, а при
t > |x0|/v − только второй член, описывающий движение частицы в
обратном направлении. В области х > а частица появляется с заметной вероятностью
только при t > |x0|/v и в дальнейшем движется все время вправо,
удаляясь от барьера. Все эти результаты проиллюстрированы на рис. 7.1, где
изображено распределение координат частицы ρ(х,t) = |k(x,t)|2 для
различных моментов времени; стрелки указывают направление движения частицы.
Коэффициент прохождения частицы через барьер есть, очевидно, вероятность найти
частицу в области х > а при t >> t0:
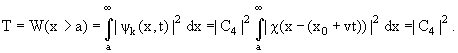 |
(7.19) |
Аналогично вычисляется и коэффициент отражения:
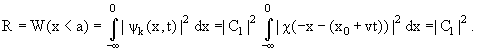 |
(7.20) |
Это, действительно, тот же результат (7.4), к которому мы
пришли раньше, пользуясь стационарной теорией. Заметим, что функциям ψk(x),
к нахождению которых сводится вычисление коэффициентов прохождения и отражения,
в нестационарной теории можно не придавать никакого физического смысла; во
всяком случае, не будучи квадратично-интегрируемыми функциями, они не описывают
никаких реальных состояний частицы.
Прежде чем перейти к трехмерному случаю, напомним, что мы
специально так подобрали параметры начального состояния частицы, чтобы
пренебречь расплыванием волнового пакета за время его движения к барьеру. Та же
задача в условиях сильного распльтания пакета оказывается гораздо более сложной
и требует специального рассмотрения. |