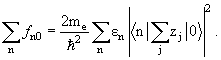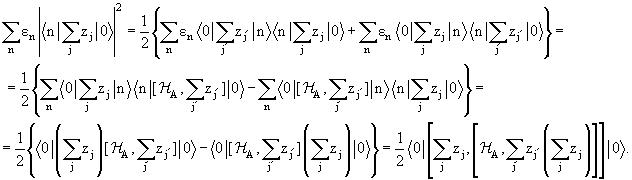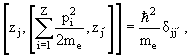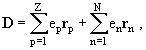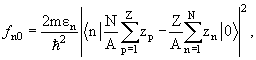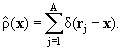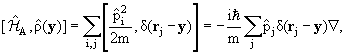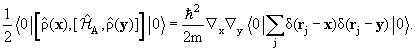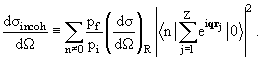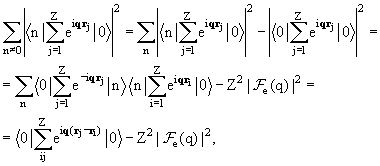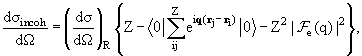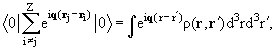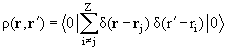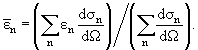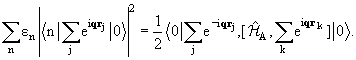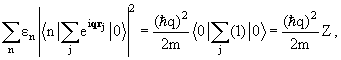Лекция 9. Правила сумм в теории столкновений. Приближение полноты

§ 9.1. Роль правил сумм в атомной и ядерной физике. «Динамические» правила сумм в теории столкновений

    Правила сумм − это особого рода интегральные соотношения для вероятностей возбуждения многочастичных систем, основанные на свойстве полноты их волновых функций. Особую ценность представляют правила сумм, носящие модельно независимый характер.
    Примером является известное правило сумм для атомного фотоэффекта.
    Пусть ƒ_n0 − сила осциллятора (8.60) электромагнитного Е1 −перехода |0> → |n>. Вычислим сумму значений ƒ_n0 по всем возбужденным состояниям атома, относящимся и к дискретному, и к непрерывному спектру:

(9.1)

Для этого воспользуемся соотношением (8.2), где в качестве оператора _А возьмем гамильтониан изолированного атома:

(9.2)

Учитывая, что ε_n − это энергия возбуждения атома, отсчитываемая от его основного состояния
(ε₀ = 0), заметим, что для любого оператора , взятого в обкладках собственных состояний оператора _А, справедливы тождества:

εn<n||0> = <n|[А,]|0>, εn<0||n> = −<0|[А,]|n>.

(9.3)

Используя их, произведем тождественные преобразования суммы (9.1):

(9.4)

    Таким образом, сумма сил осцилляторов по бесконечному полному набору возбужденных состояний сводится к среднему значению двойного коммутатора [_z,[_А,_z] в основном состоянии атома.
    При вычислении этого среднего воспользуемся тем, что оператор кулоновского взаимодействия электронов с ядром и электронов между собой коммутирует с оператором координат электрона:

остальная часть двойного коммутатора вычисляется явно:

(9.6)

В итоге получаем

(9.7)

Соотношение (9.7) для многоэлектронного атома называется правилом сумм Томаса − Райхе − Куна.
    В качестве другого примера рассмотрим правило сумм для электрических дипольных переходов в ядрах.
    Оператор электрического дипольного момента ядра имеет вид

(9.8)

где r_р и r_n − операторы координат протонов и нейтронов, а е_р и е_n − эффективные заряды нуклонов в Е1 −переходах, которые, как известно из ядерной физики, имеют значения:

Определим силу осциллятора парциального Е1 −перехода в ядре по аналогии с (8.60):

(9.10)

где m − это теперь масса нуклона. Суммирование сил осцилляторов по всем возбужденным состояниям ядра производится в принципе так же, как это было сделано выше для атома. Однако при вычислении двойного коммутатора [D,[,D]], аналогичного тому, что получен в (9.4), появляются существенные различия. Благодаря наличию обменных сил между нуклонами оператор полной потенциальной энергии ядра не коммутирует, вообще говоря, с оператором координат нуклона. Поэтому сумма сил осцилляторов в ядре не сводится, в общем случае, к какому-либо модельно независимому выражению. Лишь если пренебречь обменным взаимодействием, можно получить результат того же типа, что и соотношение (9.7):

(9.11)

    Применяя квантовую теорию столкновений к описанию ядерных реакций или атомных процессов, мы часто обращаемся непосредственно к правилам сумм (9.7) или (9.11), используя предельные соотношения типа (8.61), которые связывают вероятность парциальных переходов в атомах или ядрах под действием налетающих частиц с соответствующими силами осцилляторов. Большое распространение получили также так называемые динамические правила сумм, устанавливаемые для операторов, которые, в отличие от рассмотренных выше операторов дипольного момента атома или ядра, зависят от переданного импульса или других динамических параметров, характеризующих процесс столкновения. Рассмотрим одно из таких соотношений.
    Пусть ρ_n0(x) − переходная плотность, связывающая основное и возбужденное состояния некоторой составной системы. Используя (9.3), легко доказать тождество

(9.12)

где х и у − произвольные точки, а (х) − оператор плотности частиц в точке х:

(9.13)

Если гамильтониан _А имеет вид (9.2) и, в частности, не содержит обменных операторов, то двойной коммутатор в правой части формулы (9.12) вычисляется непосредственно:

(9.14)

и далее

(9.15)

В итоге мы получаем правило сумм для переходных плотностей (T.LDeal, S.Fallieros, 1973):

(9.16)

здесь ρ₀(x) = <0|(x)|0> − функция распределения плотности частиц в основном состоянии системы.
    Из формулы (9.16) вытекает ряд полезных соотношений более частного характера. Рассмотрим переходы, возбуждаемые некоторым возмущением, которому соответствует локальный оператор следующей формы:

(9.17)

(такие операторы, представляющие собой сумму идентичных слагаемых по всем частицам, называются одночастичными). В соответствии с определением (9.13) выразим через оператор плотности частиц:

= ∫ƒ(x)p(x)d3x .

(9.18)

Комбинируя соотношения (9.16) и (9.18), легко получить

(9.19)

    Записанное в импульсном представлении соотношение (9.19) становится правилом сумм для неупругих формфакторов. Выбирая в качестве различные операторы мультипольных моментов системы, можно получить правила сумм для соответствующих мультипольных формфакторов (см. упр. 9.2).

§ 9.2. Некогерентное рассеяние быстрых электронов на атомах. Связь вероятности рассеяния с парной корреляционной функцией

    Часто дифференциальное сечение рассеянных быстрых протонов на ядрах измеряется в условиях, когда недостаточная чувствительность детекторов или недостаточная монохроматизация падающего пучка не позволяет разделить вклады отдельных парциальных переходов. Имея в виду такие измерения, вычислим вероятность неупругого рассеяния электронов атомом безотносительно к тому, в каком состоянии остается атом после столкновения. По-прежнему будем пользоваться борновским приближением.
    Итак, речь идет о величине

(9.21)

где суммирование охватывает все возбужденные состояния атома как дискретного, так и непрерывного спектра. Значок «incoh» соответствует термину «некогерентный», смысл которого в данном случае мы увидим чуть ниже. Подставляя в качестве дифференциального сечения парциального перехода dσ_n/dΩ выражение (8.39), получаем

(9.22)

Эта формула записана не совсем точно; при фиксированных значениях энергии (импульса) падающих электронов и угла рассеяния (что соответствует стандартной постановке эксперимента) величина импульса рассеянного электрона, а также переданный импульс (который, не будем забывать, входит не только в показатель экспоненты, но и в фактор (dσ_n/dΩ)_R), зависят от энергии возбуждения атома ε_n в конечном состоянии. Таким образом, строго говоря, индекс конечного состояния атома |n> следовало бы приписать величинам p_f, q и (dσ_n/dΩ)_R входящим в (9.22). Мы, однако, пренебрежем этой зависимостью, для чего примем, что средняя энергия возбуждения атома много меньше, чем энергия налетающих электронов, а угол рассеяния мал:

n << Е,   θ << 1 .

(9.23)

При таком условии из (8.55) и (8.11) получаем

(9.24)

направление вектора q при выполнении условия (9.23) также не зависит от ε_n.
    Полагая далее, что в (9.22) входят некоторые средние значения q и (dσ_n/dΩ)_R), выполним суммирование по n, учитывая свойство полноты состояний атома:

(9.25)

здесь _e(q) − формфактор плотности электронов в основном состоянии атома (см. 8.31). Подставляя (9.25) в (9.22) и выделяя в двойной сумме ∑_ij члены с j = i окончательно получаем

(9.26)

    Проанализируем полученное выражение. Общие свойства упругих формфакторов атомов _e(q) бьши рассмотрены в предыдущей лекции. Мы видели, в частности, что скорость его убывания с ростом q определяется, прежде всего, средними размерами атома а. Все многочастичные эффекты атомной структуры проявляются в свойствах упругих формфакторов как эффекты высших порядков на фоне основных особенностей, определяемых распределением средней плотности заряда. Что касается второго слагаемого входящего в (9.26), то его поведение в зависимости от q непосредственно определяется характером парных корреляций между электронами в основном состоянии атома. Это хорошо видно из следующего фурье-преобразования:

(9.27)

где

(9.28)

парная корреляционная функция электронов в атоме.
    Свойства парной корреляционной функции атома или ядра характеризуются в первую очередь величиной среднего относительного расстояния между двумя частицами («корреляционная длина»), на котором их движение не является независимым. Корреляция между двумя частицами может быть обусловлена их непосредственным («остаточным») взаимодействием, не вошедшим в среднее самосогласованное поле атома или ядра; таково, например, сильное отталкивание между нуклонами в ядре на малых расстояниях. В таком случае корреляционная длина l_c это, по существу, радиус остаточного взаимодействия. Большое значение для структуры атомов и ядер имеют так называемые паулевские корреляции, которые связаны с эффективным отталкиванием частиц на близких друг к другу расстояниях, связанных с принципом Паули (см. упр. 9.3).
    Итак, в условиях (9.23) дифференциальное сечение неупругого рассеяния быстрых электронов, просуммированное по всем возбужденным состояниям атома, определяется распределением электронной плотности и свойствами парной корреляционной функции в основном состоянии атома. При больших переданных импульсах (q >> 1/а; q >> l/l_c) и второй, и третий члены в (9.26) пропадают:

т.е. падающий электрон рассеивается атомом как системой независимых Z электронов. Это и объясняет введенный нами термин «некогерентное рассеяние».

§ 9.3. Средняя энергия, теряемая частицей при некогерентном рассеянии. Понятие квазисвободного взаимодействия

    Пусть быстрая частица неупруго рассеивается мишенью (атомом, ядром), содержащей N частиц одинаковой массы т. Продолжая рассмотрение, начатое в предыдущем параграфе, вычислим, пользуясь борновским приближением, среднюю энергию, которую теряет быстрая частица на возбуждение мишени при некогерентном рассеянии:

(9.30)

Суммирование по n в знаменателе дает сечение dσ_incoh/dΩ (формула (9.26) или (9.29)). Выполним суммирование по n в числителе. Для этого воспользуемся соотношением типа (9.4) и (9.12), которое легко вывести непосредственно с помощью условия полноты:

(9.31)

Дальнейшие непосредственные вычисления дают

(9.32)

(9.33)

где Z − число частиц, составляющих систему, с которой сталкивается падающая быстрая частица (число электронов в атоме).
    Ранее мы установили (см. (9.29)), что при больших переданных импульсах (q >> 1/а) знаменатель в (9.30) сводится к сумме дифференциальных сечений рассеяния на отдельных электронах атома. Подставляя (9.29) и (9.33) в (9.30), получаем

|q>>1/а = (ћq)2/(2m) .

(9.34)

Соотношение (9.34) еще глубже раскрывает характер некогерентного рассеяния: средняя энергия, потерянная частицей при столкновении, определяется просто величиной потерянного ею импульса; это есть кинетическая энергия одной из частиц мишени, принявшей на себя весь импульс q. Таким образом, при больших переданных импульсах некогерентное рассеяние ярко обнаруживает − независимо от конкретных свойств волновых функций системы − черты «квазисвободного» («квазиупругого») взаимодействия налетающей частицы с отдельными частицами, составляющими мишень.
    Средняя энергия, потерянная частицей, − это основная, самая простая характеристика процесса некогерентного рассеяния. Более детальное представление о процессе рассеяния, а также о свойствах мишени, с которой происходит столкновение, можно получить, исследуя ширину разброса потерянной энергии вокруг ее среднего значения. Количественно ее можно охарактеризовать с помощью дисперсии распределения:

(9.35)

В отличие от средней потерянной энергии величина дисперсии D_ε, сильно зависит от свойств системы (мишени), с которой сталкивается налетающая частица. С помощью условия полноты можно, в частности, показать, что величина D_ε, тем больше, чем больше средний импульс частицы мишени в основном состоянии мишени (см. упр. 9.4).

Упражнения

9.1. Получить соотношение (9.11).

9.2. Используя (9.19), получить динамическое правило сумм для монопольных переходов (Е.Т. Као, S. Fallieros, 1970):

(9.36)

здесь − матричный элемент оператора монопольного перехода, _n0(q) − соответствующий переходный формфактор, (q) − формфактор плотности частиц в основном состоянии.

9.3. Вычислить корреляционный интеграл

для ферми-газа одинаковых частиц с массой m. Указать параметр, играющий роль корреляционной длины l_c. Оценить величину  l_c для ядерного вещества, рассматривая его как ферми-газ нуклонов.

9.4. Быстрые электроны рассеиваются заряженной частицей массы т, удерживаемой вблизи точки
r = 0 упругой силой. Пользуясь борновским приближением и считая, что энергия кванта колебаний ћω много меньше, чем энергия налетающего электрона, исследовать форму энергетического спектра рассеянных электронов при малых и при больших переданных импульсах. Как зависит ширина разброса потерянной электроном энергии от свойств основного состояния осциллятора?