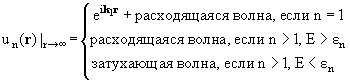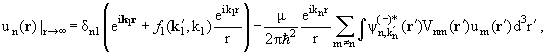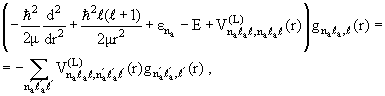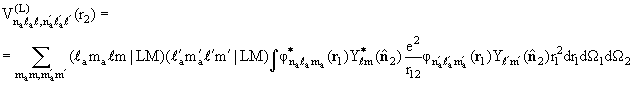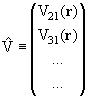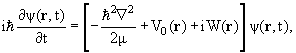Лекция 10. Основные понятия многоканальной теории рассеяния
§ 10.1. Уравнения метода сильной связи каналов.
Асимптотические условия
Рассмотрим процесс столкновения (8.1), не прибегая
к упрощениям, свойственным теории возмущений. Пусть, как и в § 8.1,
ξ − это набор внутренних переменных мишени А, а r − пространственная
координата частицы х, которая сталкивается с мишенью. По-прежнему пренебрежем
тождественностью частиц, спиновыми эффектами и эффектами отдачи.
Оператор взаимодействия частицы с мишенью
 = =
 (ξ,r),
вообще говоря, недиагонален по состояниям мишени |n>. Значит, взаимодействие
частиц с мишенью может переводить мишень из одного состояния в другое,
причем, когда это взаимодействие достаточно велико, мишень, обмениваясь
энергией с частицей х, может совершать такие переходы многократно, пока
не окажется в том или ином конечном состоянии. Пусть частица х сталкивается
с мишенью, находящейся в основном состоянии |0>. Если в результате столкновения
мишень останется по-прежнему в основном состоянии, т.е. если происходит
упругое рассеяние х + А → х + А, то будем говорить, что в конечном состоянии
мы имеем систему х + А в упругом канале.
Если мишень перешла в какое-то другое состояние |n> ≠ |0> (неупругое
рассеяние х + А → х' + А*), то будем говорить, что в конечном
состоянии мы имеем систему х + А в неупругом
канале. (ξ,r),
вообще говоря, недиагонален по состояниям мишени |n>. Значит, взаимодействие
частиц с мишенью может переводить мишень из одного состояния в другое,
причем, когда это взаимодействие достаточно велико, мишень, обмениваясь
энергией с частицей х, может совершать такие переходы многократно, пока
не окажется в том или ином конечном состоянии. Пусть частица х сталкивается
с мишенью, находящейся в основном состоянии |0>. Если в результате столкновения
мишень останется по-прежнему в основном состоянии, т.е. если происходит
упругое рассеяние х + А → х + А, то будем говорить, что в конечном состоянии
мы имеем систему х + А в упругом канале.
Если мишень перешла в какое-то другое состояние |n> ≠ |0> (неупругое
рассеяние х + А → х' + А*), то будем говорить, что в конечном
состоянии мы имеем систему х + А в неупругом
канале.
Понятие канала характеризует систему х + А на большом взаимном
расстоянии, когда взаимодействие частицы х с мишенью А уже не существенно.
На близком же расстоянии, там, где действует оператор
 (ξ,r),
различные каналы оказываются связанными между собой, и сказать, из в
каком из них находится система, невозможно. Теория столкновений, в которой
учитывается связь между разными каналами рассеяния, называется
многоканальной теорией рассеяния.
Вариант этой теории, в котором, без каких-либо аппроксимаций, строго
учитывается связь между ограниченным числом каналов, а влияние всех
прочих каналов просто отбрасывается, называется
методом сильной связи каналов. Получим
основные уравнения этого метода. (ξ,r),
различные каналы оказываются связанными между собой, и сказать, из в
каком из них находится система, невозможно. Теория столкновений, в которой
учитывается связь между разными каналами рассеяния, называется
многоканальной теорией рассеяния.
Вариант этой теории, в котором, без каких-либо аппроксимаций, строго
учитывается связь между ограниченным числом каналов, а влияние всех
прочих каналов просто отбрасывается, называется
методом сильной связи каналов. Получим
основные уравнения этого метода.
В стационарной теории столкновений процесс рассеяния описывается
волновой функцией всей системы х + А, удовлетворяющей стационарному
уравнению Шредингера:
 Ψ(ξ,r)
= EΨ(ξ,r), Ψ(ξ,r)
= EΨ(ξ,r), |
(10.1) |
где полный гамильтониан системы
 дается
формулами (8.5), (8.6). Волновые функции |n> = Фn(ξ,r)
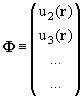
описывающие различные состояния мишени, образуют полный набор. Волновую
функцию всей системы Ψ(ξ,r) можно разложить по этому набору: дается
формулами (8.5), (8.6). Волновые функции |n> = Фn(ξ,r)
описывающие различные состояния мишени, образуют полный набор. Волновую
функцию всей системы Ψ(ξ,r) можно разложить по этому набору:
| Ψ(ξ,r) = ∑un(r)Фn(ξ), |
(10.2) |
здесь символ ∑, как и в (8.4), обозначает суммирование по дискретному
спектру и интеграл по непрерывному спектру состояний мишени (в отличие
от § 8.1 основному состоянию мишени припишем индекс n = 1; при этом
сохраним отсчет энергии системы от этого состояния, таким образом, положим
ε1 = 0). Функции un(r), зависящие от координаты
налетающей частицы r, называются канальными
функциями.
Чтобы перейти к методу сильной связи, надо оставить в (10.2)
конечное число каналов, соответствующих каким-то определенным дискретным
состояниям мишени (в том числе, конечно, и основному состоянию):
| Ψ(ξ,r) = ∑nun(r)Фn(ξ), |
(10.3) |
Для отбора состояний, наиболее существенных в каждом отдельном случае,
не существует каких-либо абсолютно четких критериев. Это зависит и от
энергии налетающих частиц, и от того, какой канал рассеяния представляет
наибольший интерес в рассматриваемой конкретной задаче. Из общих соображений
ясно, что в первую очередь следует включить в (10.3) те каналы, которые
наиболее сильно связаны взаимодействием
 (ξ,r)
с входным (упругим) и выходным каналами. Большое значение имеет также,
насколько близко расположены соответствующие уровни мишени к уровню
конечного состояния мишени или к его основному состоянию. (ξ,r)
с входным (упругим) и выходным каналами. Большое значение имеет также,
насколько близко расположены соответствующие уровни мишени к уровню
конечного состояния мишени или к его основному состоянию.
Подставим (10.2) в уравнение Шредингера (10.1). Учитывая ортонормированность
состояний |n>, получаем систему связанных уравнений для канальных функций
un(r):
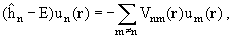 |
(10.4) |
здесь мы ввели обозначения:
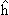 n
= n
=
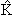 + εn + Vnn(r)
+ εn + Vnn(r) |
(10.5) |
− гамильтониан взаимодействия частицы с мишенью в n−ом канале;
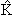 = =
 2/(2μ)
− оператор кинетической энергии частицы; 2/(2μ)
− оператор кинетической энергии частицы;
Vnm(r) = V (r)
≡ <n||m> = ∫Ф (r)
≡ <n||m> = ∫Ф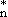 (ξ) (ξ) (ξ,r)Фm(ξ)dξ (ξ,r)Фm(ξ)dξ |
(10.6) |
− матрица оператора взаимодействия частицы х с мишенью А в обкладках
волновых функций мишени.
Система (10.4) решается со следующими асимптотическими условиями:
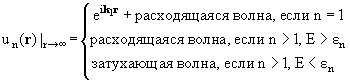 |
(10.7) |
Первая строка соответствует физическому условию, что на мишень, находящуюся
в состоянии |1>, из бесконечности падает поток частиц х с импульсом
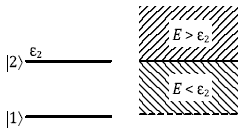
k1. Вторая строка относится к неупругим каналам, переход
в которые разрешен с точки зрения закона сохранения энергии системы:
энергия возбуждения соответствующих уровней мишени εn меньше,
чем кинетическая энергия падающих частиц на бесконечности; это так называемые
открытые каналы. Третья строка относится к
закрытым каналам; энергии падающей частицы Е недостаточно,
чтобы перевести мишень в соответствующее возбужденное состояние.
С математической точки зрения система (10.4) представляет собой
систему связанных дифференциальных уравнений 2-го порядка. Легко показать,
что она вместе с дополнительными условиями (10.7), эквивалентна системе
интегральных уравнений:
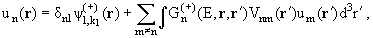 |
(10.8) |
где
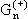 (Е,r,r'
) − функция Грина одночастичной задачи, описывающая движение
частицы х в канале n без учета его связи с другими каналами. Для нее
справедливо уравнение (1.10): (Е,r,r'
) − функция Грина одночастичной задачи, описывающая движение
частицы х в канале n без учета его связи с другими каналами. Для нее
справедливо уравнение (1.10):
(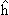 n
− E) n
− E)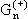 (Е,r,r'
) = δ(r −r' ). (Е,r,r'
) = δ(r −r' ). |
(10.9) |
Согласно (6.20), асимптотика функции Грина
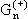 (Е,r,r'
) имеет вид (Е,r,r'
) имеет вид
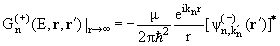 |
(10.10) |
где k'n = k'nr/r
− вектор импульса рассеянной частицы в канале n, а
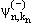 (r'
) − соответствует гамильтониану (r'
) − соответствует гамильтониану
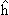 n
и удовлетворяет, вместе с n
и удовлетворяет, вместе с
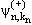 (r),
уравнению (r),
уравнению
(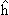 n
− E) n
− E)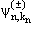 (r)
= 0 , (r)
= 0 , |
(10.11) |
Частным случаем функции
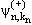 (r)
с расходящейся волной является входящая в (10.8) одночастичная волновая
функция (r)
с расходящейся волной является входящая в (10.8) одночастичная волновая
функция
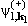 (r),
которая представляет собой точное решение задачи об упругом рассеянии
частицы на мишени, если пренебречь влиянием на него всех неупругих каналов.
Итак, многоканальная задача рассеяния допускает как дифференциальную,
так и интегральную формулировку. В обоих случаях в ее решение входит
в качестве вспомогательного элемента задача потенциального рассеяния
(10.11) − об упругом рассеяний частицы на мишени, находящейся в определенном
(не только в основном, но и в том или ином возбужденном) состоянии. (r),
которая представляет собой точное решение задачи об упругом рассеянии
частицы на мишени, если пренебречь влиянием на него всех неупругих каналов.
Итак, многоканальная задача рассеяния допускает как дифференциальную,
так и интегральную формулировку. В обоих случаях в ее решение входит
в качестве вспомогательного элемента задача потенциального рассеяния
(10.11) − об упругом рассеяний частицы на мишени, находящейся в определенном
(не только в основном, но и в том или ином возбужденном) состоянии.
|