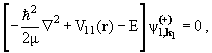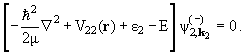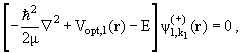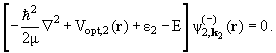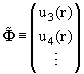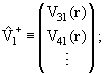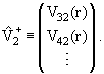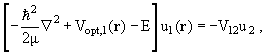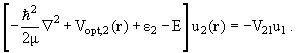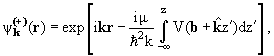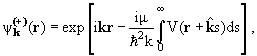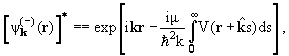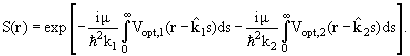§ 11.2. Метод искаженных волн и оптическая модель
В предыдущем параграфе мы получили основные формулы метода искаженных
волн, отвлекаясь от связи входного и выходного каналов с другими
каналами. Устраним этот недостаток. Забегая вперед, отметим, что
уточнение полученных выше формул (11.7), (11.9) коснется искаженных волн
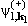 (r) и (r) и
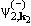 (r). Физические соображения
подсказывают, в частности, что вместо этих функций, которые вычисляются с
учетом среднего взаимодействия между частицей и мишенью, более
оправданным было бы взять искаженные волны, рассчитанные для
соответствующих комплексных оптических потенциалов во входном и выходном
каналах. Это значит, что вместо уравнений (11.8) следует решать
уравнения (r). Физические соображения
подсказывают, в частности, что вместо этих функций, которые вычисляются с
учетом среднего взаимодействия между частицей и мишенью, более
оправданным было бы взять искаженные волны, рассчитанные для
соответствующих комплексных оптических потенциалов во входном и выходном
каналах. Это значит, что вместо уравнений (11.8) следует решать
уравнения
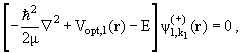
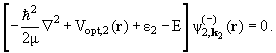 |
(11.10) |
Входящие сюда оптические потенциалы Vopt,l и Vopt,2 вообще говоря,
различаются между собой и по амплитуде и по форме как вещественной, так и
мнимой части. На практике при использовании метода искаженных волн для
описания неупругого рассеяния параметры оптического потенциала во
входном упругом канале чаще всего определяются путем подгонки под данные
об упругом рассеянии. Что касается оптического потенциала в неупругом
канале, то здесь подобная подгонка, разумеется, невозможна, и поэтому в
качестве Vopt,2(r) обычно используется тот же потенциал
Vopt,1(r).
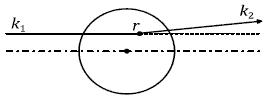
Разберем, отправляясь от общих уравнений многоканальной теории
рассеяния, насколько обоснована вся эта процедура.
Пусть нам надо вычислить дифференциальное сечение процесса А(х,х')А* с
переходом мишени из основного |1> в некоторое возбужденное состояние
|2>. Обращаясь к приему, использованному в
§ 10.4, выделим в исходной
системе уравнений (10.4) канальные функции входного u1(r) и выходного
u2(r) каналов, а из остальных функций составим столбец:
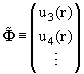 |
(11.11) |
Введем также матрицу операторов
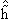 с теми же элементами
<n| с теми же элементами
<n|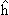 |m>, что
даются формулой (10.40), но с укороченным по сравнению с (10.40) базисом
− в него не входят каналы 1 и 2. По аналогии с (10.41) и (10.42)
введем также операторы, связывающие каждый из каналов 1 и 2 со всеми остальными каналами: |m>, что
даются формулой (10.40), но с укороченным по сравнению с (10.40) базисом
− в него не входят каналы 1 и 2. По аналогии с (10.41) и (10.42)
введем также операторы, связывающие каждый из каналов 1 и 2 со всеми остальными каналами:
 1 = (V13(r),V14(r),...) , 1 = (V13(r),V14(r),...) ,
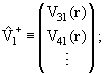 |
(11.12) |
 2 = (V23(r),V24(r),...) , 2 = (V23(r),V24(r),...) ,
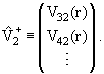 |
(11.13) |
Тогда систему уравнений (10.4) можно представить в виде
(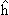 1
− E)u1 = − 1
− E)u1 = − 1 1 − V12u2 ,
− V12u2 ,
(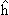 2
− E)u2 = − 2
− E)u2 = − 2 2 − V21u1 ,
− V21u1 ,
(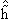 − E) − E) = −
= −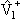 u1
− u1
−
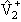 u2
, u2
, |
(11.14) |
Приступая к решению этой системы, сначала исключим из нее столбец
 : :
(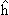 1
+ 1
+  1 1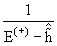 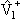 − E)u1 = −{
− E)u1 = −{ 1 1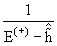 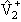 + V12}u2 ,
+ V12}u2 ,
(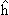 2
+ 2
+  2 2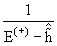 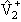 − E)u2 = −{
− E)u2 = −{ 2 2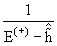 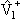 + V21}u1 .
+ V21}u1 . |
(11.15) |
Полученную систему уравнений надо решать с асимптотическим условием (10.14).
Будем искать приближенное решение этой системы, соответствующее низшему порядку теории возмущений по взаимодействию, связывающему входной и выходной каналы. Отметим
принципиальную разницу между уравнениями (11.15) и системой уравнений
(10.13) в схематической двухканальной задаче: в многоканальном случае
связь каналов 1 и 2 осуществляется не только прямо − благодаря оператору
V12 = V*21, но и косвенно, через все другие каналы
− благодаря
нелокальному оператору, стоящему в правой части уравнений (11.15).
Выпишем его в более явной форме, используя (11.12) и 11.13):
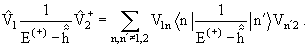 |
(11.16) |
Оператор (11.16) пропорционален произведению недиагональных матричных
элементов V1n и Vn'2, т.е. представляет собой член более высокого
порядка относительно межканального взаимодействия, чем V12. B низшем
порядке теории возмущений по межканальному взаимодействию оператор
(11.16) следовало бы из уравнений (11.15) исключить. Так мы,
действительно, и поступим, однако прежде разберем, не следует ли
одновременно исключить из уравнений (11.15) также нелокальные операторы  1(E(+) − 1(E(+) −
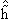 )-1 )-1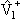 и
и  2(E(+) − 2(E(+) −
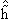 )-1 )-1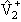 , поскольку они тоже пропорциональны произведению недиагональных матричных элементов
V1n и Vn'2, например: , поскольку они тоже пропорциональны произведению недиагональных матричных элементов
V1n и Vn'2, например:
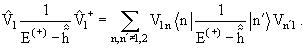 |
(11.17) |
Но тогда вообще пропадет связь каналов 1 и 2 со всеми другими
каналами, и задача сведется к двухканальной. Как же сохранить (хотя бы
приближенно) основные эффекты, обусловленные связью входного и выходного
каналов со всеми другими каналами?
Внимательное рассмотрение показывает, что для отбрасывания
недиагонального оператора
 1(E(+) − 1(E(+) −
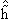 )-1 )-1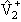 имеется больше оснований,
чем для отбрасывания диагональных операторов имеется больше оснований,
чем для отбрасывания диагональных операторов
 1(E(+) − 1(E(+) −
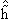 )-1 )-1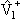 или
или  2(E(+) − 2(E(+) −
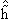 )-1 )-1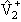 . Действительно, допустим, что матрица оператора . Действительно, допустим, что матрица оператора
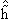 диагональна в пространстве каналов |n>. Тогда двойное
суммирование по n и n' в (11.16) и (11.17) переходит в однократное. При
этом в диагональном операторе (11.17) фаза (знак) каждого матричного
элемента V1n компенсируется фазой (знаком) входящего с ним в одно
произведение матричного элемента Vn1 = V1n*. Наоборот, в недиагональном
операторе (11.16) матричные элементы V1n и Vn2, соответствующие каждому
отдельному n, могут иметь как совпадающие, так и противоположные знаки.
Учитывая, что сумма (11.16) фактически включает бесконечное число
членов, допустим, что относительные знаки (фазы) отдельных слагаемых
меняются хаотически, так что вклады разных каналов в оператор (11.16)
полностью погашают друг друга. Назовем это приближение приближением
хаотических фаз. диагональна в пространстве каналов |n>. Тогда двойное
суммирование по n и n' в (11.16) и (11.17) переходит в однократное. При
этом в диагональном операторе (11.17) фаза (знак) каждого матричного
элемента V1n компенсируется фазой (знаком) входящего с ним в одно
произведение матричного элемента Vn1 = V1n*. Наоборот, в недиагональном
операторе (11.16) матричные элементы V1n и Vn2, соответствующие каждому
отдельному n, могут иметь как совпадающие, так и противоположные знаки.
Учитывая, что сумма (11.16) фактически включает бесконечное число
членов, допустим, что относительные знаки (фазы) отдельных слагаемых
меняются хаотически, так что вклады разных каналов в оператор (11.16)
полностью погашают друг друга. Назовем это приближение приближением
хаотических фаз.
Итак, в приближении хаотических фаз мы пренебрегаем косвенной связью
входного и выходного каналов через другие каналы по сравнению с их
прямой связью. Тогда система уравнений (11.15) принимает вид
(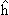 1
+ 1
+  1 1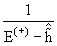 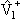 − E)u1 = −V12u2 ,
− E)u1 = −V12u2 ,
(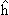 2
+ 2
+  2 2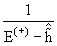 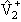 − E)u2 = −V21u1 .
− E)u2 = −V21u1 . |
(11.18) |
Если теперь сделать замену
V11
+  1 1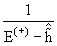 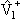 →
Vopt,1(r) , →
Vopt,1(r) ,
V22
+  2 2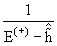 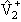 → Vopt,2(r) ,
→ Vopt,2(r) , |
(11.19) |
то мы приходим к задаче о двух каналах, однако, в отличие от задачи,
рассмотренной в § 10.2, в каждом из каналов 1 и 2 частица
взаимодействует с мишенью как с комплексным оптическим потенциалом:
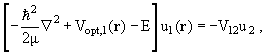
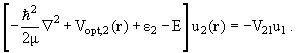 |
(11.20) |
В предыдущем параграфе было показано, что в приближении искаженных
волн решение двухканальной задачи дается формулами (11.7), (11.9).
Теперь, в отличие от (11.8), мы должны подставить в эти формулы
искаженные волны падающей и рассеянной частиц, удовлетворяющие
одночастичному уравнению Шредингера (11.10) с оптическим потенциалом.
Обсудим условия, позволяющие сделать замену (11.19). Прежде всего,
сравнивая (11.17) и (10.47), легко заметить, что нелокальный оператор
V11 +  1(E(+) − 1(E(+) −
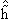 )-1 )-1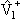 − не совсем то же самое,
что обобщенный оптический потенциал
− не совсем то же самое,
что обобщенный оптический потенциал  eff, определяющий упругое рассеяние
во входном канале 1 и аппроксимируемый модельным оптическим потенциалом
(10.48); они совпадают между собой лишь с точностью до вклада в
оптический потенциал выходного канала 2. Соответствующее различие
существует также между оптическим потенциалом Vopt,1(r), входящим в
(11.20), и оптическим потенциалом (10.48), используемым в задаче
упругого рассеяния. Правда, сама аппроксимация сложного, зависящего от энергии, нелокального обобщенного оптического
потенциала с помощью простого локального оператора (10.48)
предполагает, что в сумме (10.47) нет резко выделенных членов,
обусловленных особенно сильной связью основного состояния мишени с
каким-либо отдельным возбужденным состоянием. Поэтому, коль скоро такая
аппроксимация принята, не следует придавать большого значения
формальному различию между потенциалом Vopt,1(r) и оптическим
потенциалом (10.48). eff, определяющий упругое рассеяние
во входном канале 1 и аппроксимируемый модельным оптическим потенциалом
(10.48); они совпадают между собой лишь с точностью до вклада в
оптический потенциал выходного канала 2. Соответствующее различие
существует также между оптическим потенциалом Vopt,1(r), входящим в
(11.20), и оптическим потенциалом (10.48), используемым в задаче
упругого рассеяния. Правда, сама аппроксимация сложного, зависящего от энергии, нелокального обобщенного оптического
потенциала с помощью простого локального оператора (10.48)
предполагает, что в сумме (10.47) нет резко выделенных членов,
обусловленных особенно сильной связью основного состояния мишени с
каким-либо отдельным возбужденным состоянием. Поэтому, коль скоро такая
аппроксимация принята, не следует придавать большого значения
формальному различию между потенциалом Vopt,1(r) и оптическим
потенциалом (10.48).
Продолжая обсуждение замены (11.19), обратим внимание на различие между средними потенциалами V11(r) = <1| (ξ,r)|1) и
V22(r) = <2| (ξ,r)|1) и
V22(r) = <2| (ξ,r)|2>, относящимися к
основному и возбужденному состояниям мишени. Как правило, размеры атома
или атомного ядра в возбуждённом состоянии больше, чем в основном
состоянии. Значит, и средний потенциал V22(r) имеет более протяженный
характер, чем средний потенциал V11(r) (см. упр. 11.1). (ξ,r)|2>, относящимися к
основному и возбужденному состояниям мишени. Как правило, размеры атома
или атомного ядра в возбуждённом состоянии больше, чем в основном
состоянии. Значит, и средний потенциал V22(r) имеет более протяженный
характер, чем средний потенциал V11(r) (см. упр. 11.1).
В заключение параграфа заметим, что, конечно, систему уравнений
(11.20) можно использовать не только в качестве промежуточного этапа при
вьшоде формул метода искаженных волн, но и непосредственно − в рамках
задачи на связь двух каналов с оптическими потенциалами в каждом из этих
каналов. |