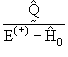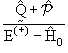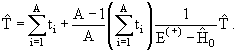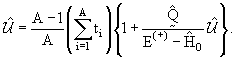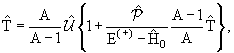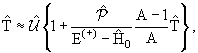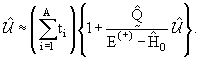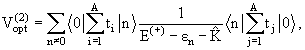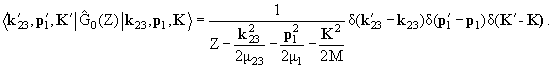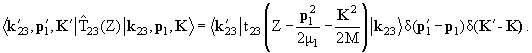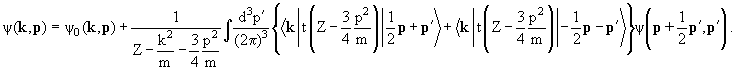Лекция 13. Многочастичная теория столкновений в t-матричной формулировке
§ 13.1. Метод Кермана − Мак-Мануса − Талера
Метод Кермана − Мак-Мануса − Талера (сокращенно: КМТ) является одним
из основных методов теории взаимодействия адронов с ядрами при высоких и
«промежуточных» энергиях. Его применение тесно связано с разработкой
общей концепции оптического потенциала. В отличие от низких энергий
«микроскопическая» теория оптического потенциала при высоких энергиях
опирается не на потенциал парного взаимодействия между налетающей
частицей и ядерными нуклонами, а на соответствующие двухчастичные
амплитуды − двухчастичные
 -операторы. В связи с этим и всю систему
уравнений, описывающих взаимодействие налетающей частицы с ядром, удобно
переформулировать на языке теории t-матрицы (см. лекцию 6). -операторы. В связи с этим и всю систему
уравнений, описывающих взаимодействие налетающей частицы с ядром, удобно
переформулировать на языке теории t-матрицы (см. лекцию 6).
Если известен потенциал взаимодействия налетающей на ядро частицы с
каждым из нуклонов ядра vi = vi(r,ri'
), то амплитуду упругого или
неупругого рассеяния частицы на ядре можно найти с помощью
 -оператора: -оператора:
F(0,k→n,k' ) ≡ Fn,0(k',k) = −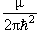 <n,k'
| <n,k'
| |0,k) ,
|0,k) , |
(13.1) |
который действует в пространстве координат частицы и внутренних координат ядра и удовлетворяет уравнению Липпмана
− Швингера:
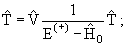 |
(13.2) |
здесь (n,k) − совокупность квантовых чисел ядра и частицы; |0> − символ основного состояния ядра;
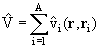 |
(13.3) |
− оператор потенциальной энергии взаимодействия частицы с ядром;
− гамильтониан невзаимодействующих между собой частицы и ядра ( A
−внутренний гамильтониан ядра; A
−внутренний гамильтониан ядра;
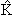 − кинетическая энергия частицы). − кинетическая энергия частицы).
Сопоставим уравнения (13.1) − (13.4) с уравнениями одночастичной
оптической модели. Согласно оптической модели, ядро действует на частицу
как объект, не имеющий внутренних степеней свободы, и их взаимодействие
описывается оптическим потенциалом
 opt, который есть оператор (вообще
говоря, нелокальный) в пространстве координат частицы. Оптический
потенциал opt, который есть оператор (вообще
говоря, нелокальный) в пространстве координат частицы. Оптический
потенциал  opt определяет волновую функцию частицы, рассеиваемой ядром: opt определяет волновую функцию частицы, рассеиваемой ядром:
(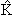 + +
 opt −
E)Ψk(r) = 0 . opt −
E)Ψk(r) = 0 . |
(13.5) |
В отличие от оператора (13.2) t-оператор оптической модели
 opt, для которого справедливо уравнение opt, для которого справедливо уравнение
также действует лишь в пространстве координат частицы.
Если взять среднее от обеих частей уравнения (13.2) по основному
состоянию ядра-мишени, то мы уравнения (13.6) не получим: оператор <0| |0> определяется бесконечной системой зацепляющихся уравнений
|0> определяется бесконечной системой зацепляющихся уравнений
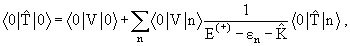
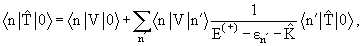 |
(13.7) |
куда кроме среднего <0|V|0> входит вся матрица взаимодействия частицы
с ядром <n|V|n' >. Значит, оптический потенциал не сводится к среднему
от потенциала (13.3) по основному состоянию ядра.
Чтобы построить для оператора <0| |0> уравнение вида (13.6), дадим
новое представление уравнению (13.2), которое эквивалентно исходному, но
удобнее его, так как позволяет более выгодно сгруппировать матричные
элементы, соответствующие упругому и неупругому рассеяниям частицы на
ядре. Для этого введем операторы
|0> уравнение вида (13.6), дадим
новое представление уравнению (13.2), которое эквивалентно исходному, но
удобнее его, так как позволяет более выгодно сгруппировать матричные
элементы, соответствующие упругому и неупругому рассеяниям частицы на
ядре. Для этого введем операторы
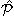 и и
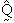 , проектирующие все операторы и
волновые функции на основное состояние ядра и ортогональное ему
подпространство всех возбужденных состояний: , проектирующие все операторы и
волновые функции на основное состояние ядра и ортогональное ему
подпространство всех возбужденных состояний:
С их помощью легко выразить
 -оператор через новый оператор -оператор через новый оператор
 («потенциальный оператор»): («потенциальный оператор»):
для которого получается уравнение
В самом деле, исключая из (13.9) и (13.10) оператор
 , мы возвращаемся к соотношению (13.2), связывающему операторы , мы возвращаемся к соотношению (13.2), связывающему операторы
 и и
 : :
 =
{1 − =
{1 −
 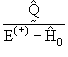  }-1 }-1
 , ,
 =
{1 − =
{1 −
 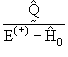  }-1 }-1
 {1+
{1+
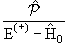  }, },
{1 −
 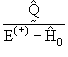  } } =
=  {1+ {1+
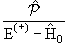  }, },
 = =
 + +
 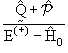  ;
;  =
=  +
+  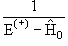  |
(13.11) |
Удобство нового представления (13.9), (13.10) заключается в том, что
среднее от U по основному состоянию ядра и есть искомый оптический
потенциал:
<0| |0> =
Vopt . |0> =
Vopt . |
(13.12) |
Действительно, если взять среднее по основному состоянию ядра от
обеих частей уравнения (13.9), то мы получим уравнение оптической модели
(13.6):
<0| |0> =
<0| |0> =
<0| |0> +
<0| |0> +
<0| |0> |0>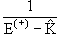 <0| <0| |0> |0> |
(13.13) |
(здесь, как и в предыдущих лекциях, мы отсчитываем энергию от основного состояния ядра-мишени, т.е.
<0| А|0> = ε0 = 0.) А|0> = ε0 = 0.)
Конечно, соотношения (13.10), (13.13) дают лишь формальное решение
задачи. Все трудности решения исходного уравнения (13.2), связанные с
суммированием по бесконечному набору возбужденных состояний ядра-мишени,
перешли теперь в уравнение (13.10) для потенциального оператора.
Принципиальным недостатком изложенного формализма является то, что мы
отправлялись от двухчастичных потенциалов взаимодействия между
налетающей на ядро частицей и нуклоном ядра-мишени. Такой подход, по
крайней мере, «неэкономен», так как для протонов, нейтронов или мезонов
высоких энергий надо сначала построить сами эти потенциалы, исходя
из амплитуд соответствующего двухчастичного взаимодействия, параметры которых
определяются непосредственно из эксперимента. Поэтому мы поступим
наоборот − перестроим уравнения (13.9) (13.10), введя в них вместо
двухчастичных потенциалов vi двухчастичные t-матрицы ti.
Строго говоря, двухчастичная t-матрица, описывающая рассеяние
падающей частицы на нуклоне ядра, и t-матрица, описывающая рассеяние
частицы свободным нуклоном, − это не одно и то же. Первая (обозначим ее τi, если частица рассеивается на
i-м нуклоне) удовлетворяет уравнению
того же вида, что (13.2):
τi = vi + vi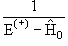 τi τi |
(13.14) |
тогда как t-матрица рассеяния на свободном нуклоне ti удовлетворяет
обычному двухчастичному уравнению Липпмана − Швингера, кудtiа не входит
гамильтониан ядра-мишени
 А. Физическое различие между операторами ti
и τi заключается в том, что пространство состояний, в которые при
взаимодействии с налетающей частицей может перейти ядерный нуклон, уже,
чем пространство конечных или промежуточных состояний для свободного
нуклона. Это связано главным образом с тождественностью ядерных
нуклонов, с принципом Паули. Мы продолжим изложение метода КМТ в
упрощенном варианте: будем считать, что с точки зрения взаимодействия с
налетающими частицами нуклон, находящийся в ядерном веществе, не
отличается от свободного нуклона, т.е. положим ti = τi. Итак, перепишем
уравнение (13.14) для операторов ti: А. Физическое различие между операторами ti
и τi заключается в том, что пространство состояний, в которые при
взаимодействии с налетающей частицей может перейти ядерный нуклон, уже,
чем пространство конечных или промежуточных состояний для свободного
нуклона. Это связано главным образом с тождественностью ядерных
нуклонов, с принципом Паули. Мы продолжим изложение метода КМТ в
упрощенном варианте: будем считать, что с точки зрения взаимодействия с
налетающими частицами нуклон, находящийся в ядерном веществе, не
отличается от свободного нуклона, т.е. положим ti = τi. Итак, перепишем
уравнение (13.14) для операторов ti:
ti = vi +vi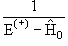 ti ti |
(13.15) |
Теперь, исключив vi из уравнений (13.2) и (13.15), выразим t-оператор
(13.2) непосредственно через двухчастичные i-матрицы свободных частиц:
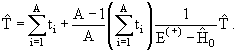 |
(13.16) |
Далее, действуя по аналогии с (13.11), выразим
 через новый
потенциальный оператор через новый
потенциальный оператор
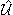 , отличный от оператора (13.10) и определяемый
уравнением , отличный от оператора (13.10) и определяемый
уравнением
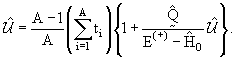 |
(13.17) |
Он связан с оператором
 соотношением соотношением
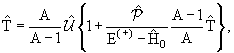 |
(13.18) |
Здесь 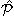 и и
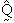 − проекционные операторы (13.8). − проекционные операторы (13.8).
В отличие от (13.9) уравнение (13.18) не является в строгом смысле
уравнением типа Липпмана − Швингера и совпадает с ним лишь с точностью
до членов порядка 1/А. Мы проанализируем далее систему уравнений (13.17)
и (13.18) для случая А >>1:
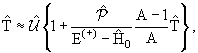 |
(13.19) |
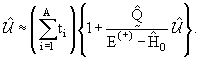 |
(13.20) |
Взяв среднее по основному состоянию ядра-мишени от обеих частей
уравнения (13.19), мы получаем уравнение оптической модели (13.6) с
оптическим потенциалом:
Vopt = <0| |0>
, |0>
, |
(13.21) |
Разложим оптический потенциал по кратности столкновений:
Vopt =
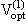 +
+
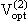 + ... ,
+ ... , |
(13.22) |
где потенциал первого порядка есть среднее от суммы двухчастичных t-операторов по основному состоянию ядра:
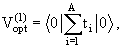 |
(13.23) |
потенциал второго порядка представляет собой однократную сумму по всем состояниям ядра, кроме основного:
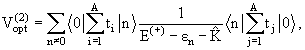 |
(13.24) |
и т.д.
Формулы (13.22) − (13.24) являются основными рабочими формулами метода КМТ.
|