Испарительная модель Вайскопфа - Ивинга
Вайскопф и Ивинг для описания
дифференциальных сечений реакции вида
a + A  C C b + B b + B
в области перекрывающихся резонансов
(Г >> D) предложили феноменологическую
модель. Ими был использован принцип
детального баланса для усредненных по времени
вероятностей переходов
где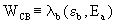 -
вероятность вылета в единицу времени из
составного ядра с энергией возбуждения Ea
частицы b с энергией εb,
WBC - вероятность захвата частицы b с
энергией -
вероятность вылета в единицу времени из
составного ядра с энергией возбуждения Ea
частицы b с энергией εb,
WBC - вероятность захвата частицы b с
энергией  b
остаточным ядром B, b
остаточным ядром B,
ωс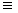 ω(Ea)
- плотность состояний составного ядра, ωB - плотность
состояний в выходном канале. ω(Ea)
- плотность состояний составного ядра, ωB - плотность
состояний в выходном канале.
 B
= ωb(εb) B
= ωb(εb) (U), (U), |
(wi.2) |
где ω(U) -плотность
состояний конечного ядра B, ωb - плотность состояний
частицы b
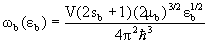 , , |
(wi.3) |
где V- некоторый произвольно большой объем, в
котором заключена система, sb,  b - спин и приведенная
масса частицы b. b - спин и приведенная
масса частицы b.
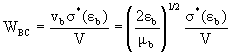 , , |
(wi.4) |
где vb - скорость частицы b,
σ*(εb) - так
называемое сечение обратной реакции - сечение
поглощения частицы b конечным ядром; первая дробь
в (wi.4) представляет из себя отношение отношение
объема цилиндра с сечением σ*(εb) и длиной
vb, т.е. объема, охваченного частицей
b за единицу времени, ко всему объему V.
Из (wi.1-4) получим для вероятности вылета
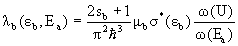 |
(wi.5) |
Дифференциальное сечение в модели испарения
имеет вид
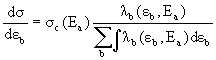 , , |
(wi.6) |
где σс(Ea) -
сечение образования составного ядра, дробь -
вероятность распада составного ядра с вылетом
частицы b с энергией εb.
В знаменателе ведется суммирование по всем
открытым при данной энергии возбуждения каналам
и интегрирование по всему определяемому законом
сохранения энергетическому диапазону.
Вся динамика процесса распада
составного ядра содержится в сечении обратной
реакции σ*(εb), которое
в частности учитывает прохождение частицы через
кулоновский барьер. Остальные сомножители
определяют доступный в реакции фазовый объем.
Основной вклад в энергетическое поведение
сечения вносит плотность
состояний конечного ядра ω(U).
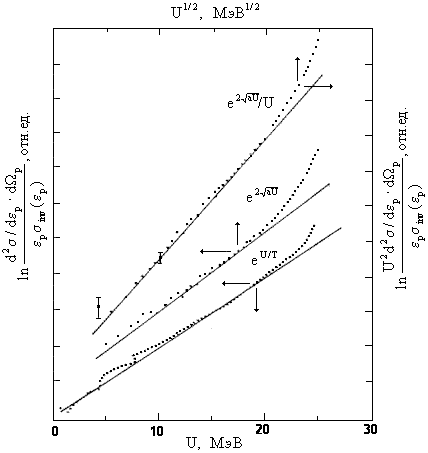
Используя выражение для плотностей
состояний ферми-газа, выражение для сечения
можно записать в виде
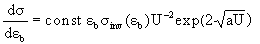 , , |
(wi.7) |
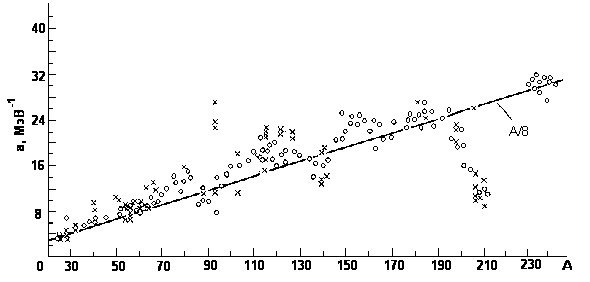
где a = ( 2/6)g - параметр
плотности уровней (g - плотность одночастичных
состояний вблизи энергии Ферми), U - энергия
возбуждения конечного ядра, εb - энергия частицы b.
Энергии вобуждения конечного ядра и энергия
частицы b связаны соотношением Ea ~
Bb + U + (AC/AB)εb, где Bb
- энергия связи частицы b, AC и AB-
массовые числа составного и конечного ядер.
Вместо сечения поглощения частицы b конечным
ядром в возбужденном состоянии
σ*(εb),
которое невозможно измерить, в расчетах
используется сечение поглощения в основном
состоянии σinv(εb). Как
показывают оценки, разница между этими
сечениями, как правило, не должна быть велика. 2/6)g - параметр
плотности уровней (g - плотность одночастичных
состояний вблизи энергии Ферми), U - энергия
возбуждения конечного ядра, εb - энергия частицы b.
Энергии вобуждения конечного ядра и энергия
частицы b связаны соотношением Ea ~
Bb + U + (AC/AB)εb, где Bb
- энергия связи частицы b, AC и AB-
массовые числа составного и конечного ядер.
Вместо сечения поглощения частицы b конечным
ядром в возбужденном состоянии
σ*(εb),
которое невозможно измерить, в расчетах
используется сечение поглощения в основном
состоянии σinv(εb). Как
показывают оценки, разница между этими
сечениями, как правило, не должна быть велика.
|
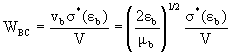 ,
,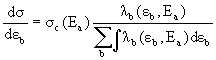 ,
,