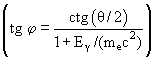Семинар 2. Квантовые свойства излучения и частиц Представления о дискретной
структуре материи зародилось в XIX веке.
2.1. Излучение абсолютно черного тела. Формула Планка
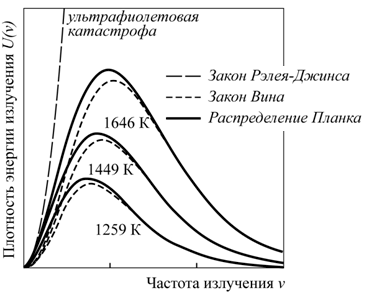
В классической физике плотность излучения абсолютно черного тела описывается законом Рэлея-Джинса
где ν − частота излучения, k − постоянная Больцмана, T − абсолютная температура.
В области низких частот формула Рэлея-Джинса хорошо описывает
экспериментальные данные. Однако в области высоких частот расхождения с
экспериментом были настолько существенны, что возникшую ситуацию стали называть
«ультрафиолетовой катастрофой».
где k – постоянная Больцмана, T – абсолютная температура, ν – частота излучения, h – постоянная Планка h = 6.62·10-34 Дж·с = 6.62·10-27 эрг·с. В квантовой теории чаще используют приведенную постоянную Планка ћ ћ = h/2π = 1.05·10-34Дж·с = 6.58×10-22 МэВ·с, которая также называется постоянной Планка.
Через пять лет
А. Эйнштейн, обобщив идею Планка, показал, что квантованность
является общим свойством электромагнитного излучения. Согласно идеям Эйнштейна
электромагнитное излучение состоит из квантов, названных позднее фотонами.
Каждый фотон имеет определенную энергию E
и импульс
где
Необходимо помнить, что истинной длиной волны является λ, а не
3.2. ФотоэффектФотоэффект был открыт Г. Герцем в 1887 г. и подробно исследован А.Г. Столетовым. При облучении металлической поверхности светом из неё вылетают электроны. Было установлено, что энергии вылетающих электронов не зависят от интенсивности излучения и определяются только его частотой. Кинетическая энергия электрона Te, вылетающего из металла под действием фотона с энергией ћω
где Aвых – работа выхода металла. Эта формула была написана Эйнштейном в 1905 г. примерно через полтора десятка лет после первых экспериментов А.Г. Столетова. Представления о квантованности электромагнитного излучения позволили объяснить закономерности фотоэффекта. 3.3. Эффект КомптонаНа основе квантовой теории А. Комптоном было объяснено явление упругого рассеяния электромагнитного излучения на свободных электронах, сопровождающееся увеличением длины волны излучения (эффект Комптона). Из законов сохранения энергии и импульса следует формула Комптона для изменения длины волны фотона Δλ, рассеянного под углом θ,
где
λ
и λ' – соответственно длины волн падающего и рассеянного фотона,
Рис. 2.2 Спектры рассеянного излучения для трех углов рассеяния.
Абсцисса пропорциональна длине излучения, ордината – интенсивности излучения. а)
Спектр падающего излучения; б) – г) спектры рассеянного на графите излучения.
3.4. Корпускулярно-волновой дуализмВажным этапом в становлении современного понимания структуры материи стала выдвинутая де Бройлем в 1924 г. гипотеза об универсальности корпускулярно-волнового дуализма. Согласно этой гипотезе не только фотоны, но и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами. Де Бройль предложил, что каждой частице, движущейся с импульсом р, следует приписать определённую длину волны – дебройлевскую длину волны. Соотношения, связывающие корпускулярные и волновые свойства частиц те же, что были установлены ранее для фотонов
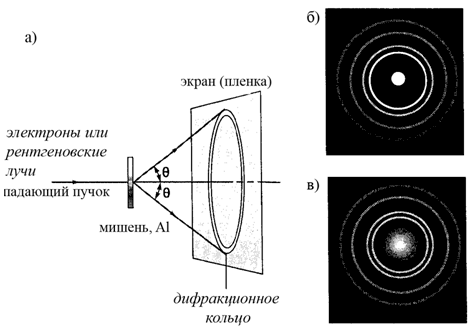
Опытами, подтверждающими идею корпускулярно-волнового дуализма, были опыты по дифракции электронов на монокристаллах. 3.5. Дифракция электроновВ 1927 г. Дж. Томсон исследовал прохождение электронов с энергией от 10 до 40 кэВ через тонкую металлическую фольгу и наблюдал дифракционную картину, аналогичную дифракционной картине фотонов соответствующих энергий. Рис. 3.3. Опыт Томсона. а) Схема установки для наблюдения дифракции на поликристаллической алюминиевой мишени. б) Дифракционная картина, полученная при рассеянии рентгеновских лучей λ = 0.071 нм. в) Дифракционная картина, полученная при рассеянии электронов с энергией 600 эВ (увеличена в 1.6 раза для сравнения с б)). Дифракционная картина
наблюдалась в опытах К. Дэвиссона и
Л. Джермера (1927 г.) по изучению отражения
электронов от монокристалла никеля. Дифракция появлялась в результате рассеяния
электронов на атомах в узлах кристаллической решетки.
3.6. Принцип неопределенности ГейзенбергаЭкспериментальное подтверждение идеи корпускулярно-волнового дуализма привело к пересмотру привычных представлений о движении частиц и способа описания частиц. Для классических материальных точек характерно движение по определенным траекториям, так, что их координаты и импульсы в любой момент времени точно определены. Для квантовых частиц это утверждение неприемлемо, так как для квантовой частицы импульс частицы связан с ее длиной волны, а говорить о длине волны в данной точке пространства бессмысленно. Для квантовой частицы нельзя одновременно точно определить значения ее координат и импульса. Неопределенность в значении координаты частицы Δx и неопределенность в значении компоненты импульса частицы Δрx связаны соотношением неопределенности, установленным В. Гейзенбергом в 1927 году
Физический смысл соотношения неопределённости (принципа неопределенности) состоит в том, что невозможно одновременно точно определить положение частицы (x,y,z) и её импульс |
 .
= 2
.
= 2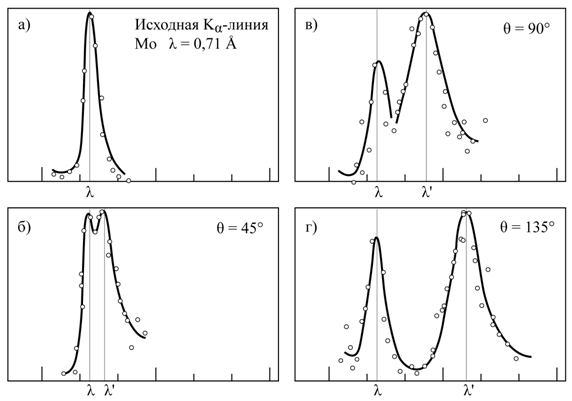
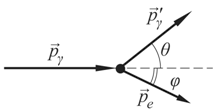 Упругое
рассеяние фотона на электроне.
Упругое
рассеяние фотона на электроне.