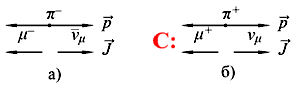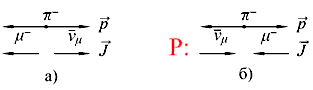Семинар 7. Взаимодействие
частиц
Реакции между частицами приводят к образованию новых частиц в результате всех
трех типов взаимодействия – сильного, электромагнитного и слабого. Вероятности
образования различных частиц определяются законами сохранения и константами
взаимодействий. С наибольшими сечениями (σ ~1 барн) образуются частицы в результате сильного
взаимодействия, сечение электромагнитных взаимодействий имеет
характерные величины на два порядка меньше. Характерные величины сечений
слабого взаимодействия ~10-19 барн. При этом
необходимо помнить, что сечение взаимодействия частиц зависит от энергии
сталкивающихся частиц.
- 7.1. Взаимодействия частиц
- 7.2. Законы сохранения
- 7.3. Пространственная четность
- 7.4. Зарядовая четность
-
Задачи
7.1. Взаимодействия частиц
В Стандартной Модели взаимодействия частиц описываются
с учетом трех фундаментальных сил. Некоторые существенные свойства
взаимодействий приведены в таблице:
| |
Слабое |
Электромагнитное |
Сильное |
| Действует на: |
аромат |
Электрический заряд |
Цветовой заряд |
| Взаимодействующие фермионы |
Кварки, лептоны |
Кварки, заряженные лептоны |
Кварки |
| Характерное время взаимодействия, с |
~10-10 |
~10-18 |
10-21 – 10-23 |
| Радиус взаимодействия, см |
~10-16 |
∞ |
~10-13 |
| Сила, отнесенная к электромагнитной, для двух
u-кварков на расстоянии: |
10-18 см |
0.8 |
1 |
25 |
| 2·10-17 см |
10-4 |
1 |
60 |
Из сравнения свойств фундаментальных сил видно, что
наиболее вероятны реакции, протекающие за счет сильного взаимодействия, затем
идут электромагнитные процессы, и наименее вероятны реакции за счет слабого
взаимодействия. Однако возможность осуществления той или иной реакции
ограничивается набором законов сохранения, и для разных взаимодействий эти
ограничения различаются.
7.2. Законы сохранения
Процессы взаимодействия частиц подчиняются определенным
законам сохранения физических величин. В таблице перечислены данные законы и
указано, в каком типе фундаментальных взаимодействий данная характеристика
сохраняется. Некоторые законы сохранения аддитивны (A), т. е. в процессе
взаимодействия сохраняется суммарная величина соответствующих характеристик или
квантовых чисел. Например, во всех взаимодействиях сохраняется сумма энергий
частиц. Ряд законов сохранения имеет мультипликативный характер (M) − в данных
процессах сохраняется произведение соответствующих характеристик (квантовых
чисел). Законы сохранения обусловлены свойствами симметрии взаимодействий.
ЗАКОНЫ СОХРАНЕНИЯ
| Характеристика |
Взаимодействие |
| Сильное |
Электромагнитное |
Слабое |
| Аддитивные законы сохранения |
| Электрический заряд, Q |
+ |
+ |
+ |
| Энергия, E |
+ |
+ |
+ |
| Импульс, p |
+ |
+ |
+ |
| Угловой момент, J |
+ |
+ |
+ |
| Барионный заряд, B |
+ |
+ |
+ |
| Лептонные заряды*, Le, Lμ,
Lτ |
+ |
+ |
+ |
| Странность, s |
+ |
+ |
− |
| Очарование, c |
+ |
+ |
− |
| Bottomness, b |
+ |
+ |
− |
| Topness, t |
+ |
+ |
− |
| Изоспин, I |
+ |
− |
− |
| Проекция изоспина, I3 |
+ |
+ |
− |
| Мультипликативные законы сохранения |
| Р-четность, P |
+ |
+ |
− |
| С-четность |
+ |
+ |
− |
| CP-инвариантность |
+ |
+ |
− |
| T-инвариантность |
+ |
+ |
− |
| CPT-инвариантность |
+ |
+ |
+ |
* Имеющиеся экспериментальные данные и стандартная
электрослабая теория согласуются с абсолютным сохранением трёх отдельных
лептонных зарядов Le,
Lμ и Lτ за исключением эффектов нейтринного смешивания,
связанных с массами нейтрино и проявляющегося в нейтринных осцилляциях.
Осцилляции приводят к нарушению законов сохранения лептонных зарядов по
отдельности, но полный лептонный заряд ∑(Le+
Lμ + Lτ) сохраняется. Вероятность нарушений сохранения Le, Lμ
и Lτ мала, эти нарушения, по существу, не
наблюдаемы, и законом сохранения отдельных лептонных чисел пользоваться можно.
Законы сохранения для всех реакций
сильного взаимодействия выполняются без исключений. Это одновременно означает
наибольшую, по сравнению с другими силами, степень симметрий этих
взаимодействий.
Слабые взаимодействия могут
происходить с превращением кварков одного аромата (flavor)
в кварки другого. Поэтому в таких слабых распадах могут не сохраняться ни
изоспин
I, ни его проекция
I3, ни квантовые числа странности s и шарма
(очарования) c. Могут нарушаться и законы сохранения квантовых чисел b (bottomness)
и t (topness).
Слабые процессы с изменением аромата кварка идут с нарушением, по крайней
мере, одного аддитивных законов сохранения: I,
I3, s, c, b, t.
При лептонных распадах в вершинах
сохраняются значения лептонных зарядов. Однако, благодаря испусканию или
поглощению
W±-бозона, может измениться заряд лептона, то есть
в рамках одного поколения могут происходить взаимные переходы между заряженным
лептоном и нейтрино.
Обмен заряженными
W+ или
W- бозонами связан с изменениями зарядов
фермионов в вершине. Диаграмма, состоящая из двух фермионных линий, вершины и
бозонной линии, называется «током». Обмен заряженными W+ или
W- бозонами реализует
заряженные токи. Обмен нейтральным Z–бозоном
соответствует взаимодействию нейтральных токов.
«Слабые» вершины, соответствующие обменам W-бозонами,
(вершины заряженных токов) обладают особенностью, которой не имеют ни «сильные»,
ни электромагнитные вершины – именно в этих вершинах происходит
превращение одного кварка в другой. Поэтому взаимопревращения адронов с
изменением кваркового состава – результат слабых взаимодействий. Например,
β-распад нейтрона, происходящий с несохранением
I3, реализуется благодаря превращению
d-кварка в u-кварк при испускании виртуального W--бозона.
|
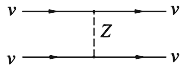
Рис. 7.1.Диаграмма слабого взаимодействия двух нейтрино одинакового аромата |
В процессах с участием нейтральных слабых токов не
изменяются ни электрические заряды участвующих частиц (лептонов и кварков), ни
ароматы участвующих фермионов. Нейтральные слабые токи истинно нейтральны, так
как истинно нейтральными частицами являются сами Z‑бозоны. В качестве примера
процесса с участием Z-бозона на рис. 7.1 приведена диаграмма слабого
взаимодействия двух нейтрино одинакового аромата.
В слабых взаимодействиях нарушаются мультипликативные
законы сохранения пространственной Р и зарядовой С четностей, а также их
произведение СР-четность.
7.3. Пространственная четность (Р-четность)
Операция пространственной инверсии
заключается в зеркальном отражении трех пространственных координатных осей. В
результате данной операции радиус-вектор
 и импульс
частицы и импульс
частицы
 меняют направление на
противоположное. Момент количества движения меняют направление на
противоположное. Момент количества движения
 не
изменяется. не
изменяется.
x, y, z,  , , 
 -x, -y, -z,
- -x, -y, -z,
- , , 
Волновая функция системы частиц
является функцией координат этих частиц. Преобразование от выбранной системы
координат к системе, соответствующей зеркальному отражению всех координатных
осей, приводит к преобразованию волновой функции системы. Оператор этого
преобразования
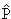 (оператор
пространственного отражения): (оператор
пространственного отражения):
где
 −
совокупность координат частиц системы: −
совокупность координат частиц системы:
 = = 1, 1,
 2,
..., 2,
..., A. A.
Если система частиц,
характеризуемая волновой функцией Ψ( ),
инвариантна к Р-преобразованию (т. е. гамильтониан системы коммутирует с
оператором пространственного отражения), то эта система характеризуется
определённой сохраняющейся чётностью р. Последняя, являясь квантовым числом,
удовлетворяет уравнению на собственные значения: ),
инвариантна к Р-преобразованию (т. е. гамильтониан системы коммутирует с
оператором пространственного отражения), то эта система характеризуется
определённой сохраняющейся чётностью р. Последняя, являясь квантовым числом,
удовлетворяет уравнению на собственные значения:
Собственные значения оператора
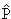 получают
двукратным применением оператора получают
двукратным применением оператора
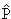 к функции Ψ( к функции Ψ( ),
которое возвращает функцию Ψ( ),
которое возвращает функцию Ψ( ) в
исходное состояние. Отсюда, с учётом (7.1) и (7.2) получаем собственные значения
квантового числа чётности р: ) в
исходное состояние. Отсюда, с учётом (7.1) и (7.2) получаем собственные значения
квантового числа чётности р:
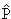 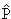 Ψ( Ψ( )
= p2Ψ( )
= p2Ψ( )
= Ψ( )
= Ψ( ),
p = ±1. ),
p = ±1.
Сильное и электромагнитное
взаимодействия инвариантны к Р-преобразованию. Поэтому
такие системы характеризуются определённой чётностью. В частности это относится
к состояниям адронов и систем адронов. В слабых взаимодействиях чётность не
сохраняется.
Распад ρ0-мезона ρ0 → π+ + π-
происходит в результате сильного взаимодействия. В результате
Р-преобразования в сильных взаимодействиях получается наблюдаемый в природе
процесс.
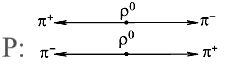
Рис. 7.2. Схема распада ρ0-мезона в СЦИ. Операция пространственного
отражения меняет направление импульсов пионов на противоположные.
Распад π-
→ μ- +
 μ происходит в
результате слабого взаимодействия. В результате Р‑преобразования изменяются
знаки импульсов и не изменяются направления спинов. μ происходит в
результате слабого взаимодействия. В результате Р‑преобразования изменяются
знаки импульсов и не изменяются направления спинов.
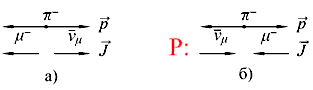
Рис. 7.3 Схема распада π–-мезона в СЦИ. а) Взаимная ориентация
импульсов и спинов продуктов распада. б) Применение операции пространственной
инверсии. Направление импульсов частиц изменилось на противоположное.
Из требования Р‑инвариантности следует равенство сечений процессов (а) и (б). В
распаде (б) образуются мюонные антинейтрино с отрицательной спиральностью,
которые в природе не наблюдаются, что означает нарушение Р‑инвариантности в
слабых взаимодействиях.
Преобразование отражения всех
координатных осей можно представить в виде поворотов всех этих осей на угол θ =
180o. Это дискретное преобразование
волновой функции частицы или системы частиц. Поэтому закон сохранения
пространственной четности – мультипликативный.
Принято указывать спин J и четность
P состояния : JP.
Чётность системы частиц определяется по формуле:
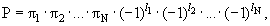 |
(7.3) |
где πi − внутренняя четность частицы,
li − орбитальный момент частицы.
Р-четность адронов
Кварки, образующие адроны, могут
находиться в состояниях с различными орбитальными моментами
lq и в
состояниях с различными значениями радиального квантового числа n. Так как кварк
имеет положительную чётность, а антикварк − отрицательную, чётности барионов и
антибарионов определяются соотношениями
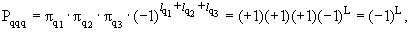
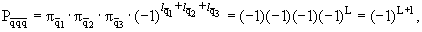
где L − результирующий орбитальный момент кварков в адроне.
Для четности мезона получаем
следующую формулу:
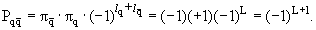
7.4. Зарядовая четность(C-четность)
Операция С
зарядового сопряжения − операция замены знаков всех зарядов на
противоположные. При этом масса, импульс и спин частицы не изменяются.
Кварк-антикварковая (q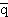 ) структура мезонов делает возможным
существование истинно нейтральных частиц.
Все аддитивные квантовые числа (электрический и барионный заряды, кварковый
аромат) в таком мезоне в сумме равны нулю. Истинно нейтральная частица
тождественна античастице. Истинно нейтральными являются π0,
η, η', ρ0, ) структура мезонов делает возможным
существование истинно нейтральных частиц.
Все аддитивные квантовые числа (электрический и барионный заряды, кварковый
аромат) в таком мезоне в сумме равны нулю. Истинно нейтральная частица
тождественна античастице. Истинно нейтральными являются π0,
η, η', ρ0,
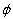 и
ω. Истинно нейтральные частицы (системы частиц) характеризуются квантовым числом
− зарядовая чётность С. и
ω. Истинно нейтральные частицы (системы частиц) характеризуются квантовым числом
− зарядовая чётность С.
Различие между операциями четности
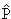 и зарядовой
четности и зарядовой
четности
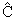 состоит в том,
что оператор зарядовой четности не всегда имеет собственное значение. Для
частицы с зарядом q, описываемой волновой функцией
|q> состоит в том,
что оператор зарядовой четности не всегда имеет собственное значение. Для
частицы с зарядом q, описываемой волновой функцией
|q>
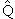 |q> = q|q> |q> = q|q>
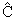 |q> |-q> |q> |-q>
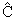 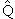 |q> = |q> = 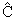 q
|q> = q q
|q> = q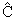 |q>
= q|-q> |q>
= q|-q>
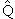 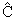 |q>
= |q>
= 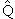 |-q> = -q|-q> |-q> = -q|-q>
(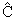 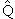 - - 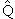 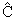 |q>
= 2q|-q> = 2 |q>
= 2q|-q> = 2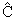 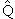 |-q> |-q>
Операторы
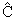 и и
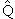 не коммутируют, т.е. не существует
состояний, которые одновременно были бы их собственными состояниями. не коммутируют, т.е. не существует
состояний, которые одновременно были бы их собственными состояниями.
|
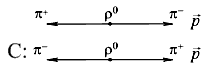
Рис. 7.4.Схема распада ρ0-мезона
в СЦИ. |
На рис. 7.4 приведена схема операции зарядового сопряжения C сильного распада ρ0-мезона ρ0→ π+
+ π−. В результате получается
наблюдаемый в природе процесс.
Схема слабого распада π−‑мезона
π− → μ− +
 μпоказана на рис. 7.5.
В результате C-преобразования получаются мюонные антинейтрино с отрицательной
спиральностью, которые в природе не наблюдаются. μпоказана на рис. 7.5.
В результате C-преобразования получаются мюонные антинейтрино с отрицательной
спиральностью, которые в природе не наблюдаются.
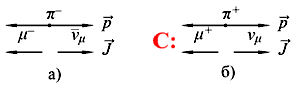
Рис. 7.5 Схема распада π−-мезона в СЦИ. а)
Взаимная ориентация импульсов и спинов продуктов распада. б) Применение операции
зарядового сопряжения.
Зарядовая
чётность С
Зарядовая
чётность сохраняется в сильных и электромагнитных
взаимодействиях и не сохраняется в слабых
взаимодействиях. |
Квант электромагнитного взаимодействия − фотон. Электромагнитное поле
описывается векторным |
![]() μпоказана на рис. 7.5.
В результате C-преобразования получаются мюонные антинейтрино с отрицательной
спиральностью, которые в природе не наблюдаются.
μпоказана на рис. 7.5.
В результате C-преобразования получаются мюонные антинейтрино с отрицательной
спиральностью, которые в природе не наблюдаются.