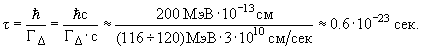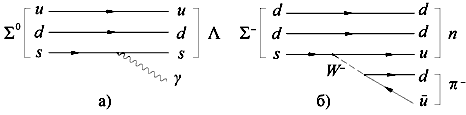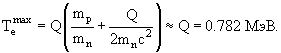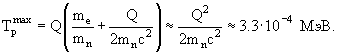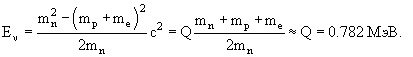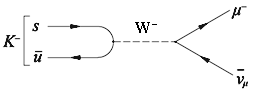Семинар 8. Распады адронов С современной точки зрения
стабильными частицами являются электрон е-, протон p,
фотон γ, три типа нейтрона ve, vµ, vτ и их античастицы e+,
8.1. Вероятность распадов Все адроны за исключением протона
являются нестабильными частицами и характеризуются способом распада и средним
временем жизни τ. Определяющим для скорости распада является фундаментальное
взаимодействие, ответственное за распад адрона. Быстрее всего − за характерное
время τ ≈ 10-23 с, происходят распады за счёт сильного взаимодействия.
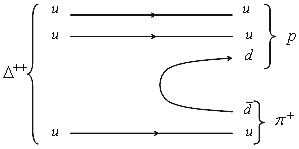
Это время отвечает сильному взаимодействию. Кварковая диаграмма распада Δ++ имеет вид:
Следующими по скорости являются
распады за счёт электромагнитного взаимодействия. Обычно это время больше
τ ≈ 10-19 с. Наконец, медленнее всего совершаются распады с участием слабых сил.
Слабые распады идут в тех случаях, когда запрещены сильные и электромагнитные
распады. Обычно времена слабых распадов >10-13 с.
Рис. 8.2. Диаграммы распадов Σ-гиперонов. а) Σ0 → Λ + γ, б) Σ− → n + π-. Помимо типа фундаментального взаимодействия на вероятность распада влияет ряд других факторов. С ростом энергии, освобождающейся при распаде, его вероятность растет. Как и реакции столкновения частиц, распады подчиняются законам сохранения. Для сильного взаимодействия выполняются все законы сохранения. В слабом взаимодействии, поскольку возможно изменение типа частиц, часть законов сохранения нарушается. 8.2. Распад нейтрона Масса нейтрона
mnc2 = 939.57 МэВ, среднее время жизни
τ(n) = 880 c.
В распаде нейтрона не сохраняется вектор
изоспина Рассчитаем энергию распада (mpc2 = 938.27 МэВ, mec2 = 0.511 МэВ, нейтрино полагаем безмассовым): Q = mnc2 − (mp + me)c2 = 0.782 МэВ > 0. Энергия реакции больше нуля, распад разрешен.
В случае распада на три частицы энергии и импульсы продуктов распада не могут быть однозначно определены, спектр вылетающих частиц носит непрерывный характер. Область возможных значений энергий продуктов реакции ограничена предельными значениями, называемыми «верхняя граница спектра». Максимальная кинетическая энергия электрона соответствует случаю, когда импульсы двух других частиц сонаправлены и направлены в противоположную сторону от импульса электрона. Тогда данный предельный случай можно рассматривать как распад нейтрона на две частицы: протон и электрон. Используя формулу (1.35) и учитывая, что Q << mnc2 и mp ≈ mn, получим, что верхняя граница спектра электронов:
Из тех же соотношений получим энергию отдачи протона:
Максимальная энергия нейтрино достигается в том случае, когда импульсы протона и электрона сонаправлены и направлены в противоположную сторону от импульса нейтрино. Тогда для максимальной энергии нейтрино можно воспользоваться соотношением (1.37):
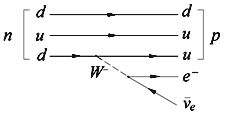
8.3. Слабые распадыПоскольку в слабых распадах изменение типа частицы может происходить только в результате испускания заряженного W-бозона, очевидно, что при этом разрешены такие переходы, в которых заряд распадающейся частицы меняется на единицу. В случае лептонов, поскольку лептонные числа сохраняются порознь, переходы между заряженными лептонами и соответствующими нейтрино происходят только внутри поколений:
Лептонные числа при этом сохраняются. В случае кварков требование изменения заряда приводит к тому, что переходы возможны только между верхними и нижними кварками и запрещены между двумя верхними или двумя нижними. С учетом масс кварков основные переходы следующие:
Видно, что при
этом квантовые числа s, c, b и
t могут изменяться только на 1. Проекция изоспина
I3 в случае распада s → u
изменяется на 1/2, в случае перехода d → u
– на единицу. n → p + e− +
или распад заряженного каона с изменением странности: K− → μ− +
Диаграмма распада K−-мезона процесса приведена на рисунке 8.4.
В полулептонных
слабых распадах странных частиц странность изменяется на единицу: Σ− → n + π−: ΔI3 = 1/2, ΔI = 1/2, Δs = 1. В данном случае суммарный электрический заряд адронов сохраняется.
|