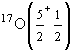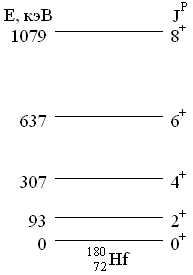Атомные ядра

Семинар 9. Атомные ядра

Открытое Резерфордом атомное ядро позволило не только объяснить строение атома, но привело к обнаружению новых типов взаимодействий.
• Сильного взаимодействия связывающего нуклоны.
• Слабого взаимодействия приводящего к взаимному превращению протонов и нейтронов.
Атомное ядро – уникальный объект позволяющий исследовать электромагнитные слабые и сильные взаимодействия на расстоянии ~10^-13 см.

9.1. N-Z диаграмма атомных ядер

9.2. Энергия связи ядра

9.3. Радиус атомного ядра

9.4. Статические характеристики атомных ядер

9.5. Модель оболочек

9.6. Возбужденные состояния атомных ядер

9.7. Мезонная теория ядерных сил

Задачи

9.1. N-Z диаграмма атомных ядер

Протоны и нейтроны образуют атомные ядра всех химических элементов. Число протонов в ядре определяет атомный номер химического элемента. Характеристики протона, нейтрона и электрона, сведены в таблицу 1.

Таблица 1

Характеристики протона, нейтрона и электрона

Характеристика	Протон	Нейтрон	Электрон
Масса mс², МэВ	938.272	939.565	0.511
Электрический заряд (в единицах элементарного заряда)	+1	0	-1
Спин (в единицах ћ)	1/2	1/2	1/2
Изоспин	1/2	1/2
Проекция изоспина	+1/2	–1/2	+1
Чётность	+1	+1
Статистика	Ферми-Дирака
Магнитный момент (для нуклонов – в ядерных магнетонах, для электрона – в магнетонах Бора)	+2.79	-1.91	+1.001
Время жизни	>10³² лет	880.3±1.1 с	>4.6·10²⁶ лет
Тип распада		n → p + e⁻ + _e

Для характеристики атомных ядер используют обозначения: число протонов Z, число нейтронов N, массовое число или число нуклонов A = Z + N. Ядра с одинаковым Z называют изотопами, а с одинаковым А – изобарами. Конкретное ядро (нуклид) обозначают ^АХ, где Х – химический символ элемента, или просто (A, Z). Например, изотоп алюминия, состоящий из 27 нуклонов, из которых 13 протонов, обозначают ²⁷Al.
Все известные ядра можно разделить на 2 группы:

Стабильные и долгоживущие ядра (всего 285). Число стабильных ядер – 264. Долгоживущими принято считать ядра с периодом полураспада T_1/2 > 5·10⁸ лет, что обеспечивает отличное от нуля процентное содержание этих ядер в естественной смеси изотопов.
Радиоактивные ядра (около 3200). Для этих ядер T_1/2 < 5·10⁸ лет.

Рис. 9.1. NZ-диаграмма атомных ядер

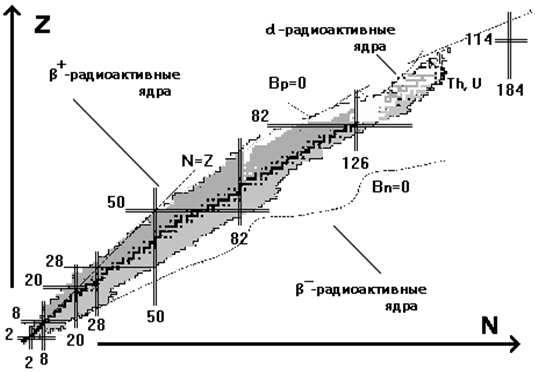
Каждому ядру на NZ-диаграмме атомных ядер соответствует определённое положение на плоскости с осями N и Z. Точками отмечены стабильные и долгоживущие ядра. Совокупность этих точек образует узкую полосу, называемую линией или долиной стабильности.
Для ядер долины стабильности отношение числа нейтронов к числу протонов

N/Z ≈ 1 + 0.015·A^2/3.

(9.1)

9.2. Энергия связи ядра

Энергия связи ядра W

W(A,Z) = [Zm_p + Nm_n – M(A,Z)]c²,

(9.2)

где m_p, m_n, M(A, Z) – массы протона, нейтрона и ядра (A,Z). Для того чтобы разделить ядро на отдельные протоны и нейтроны, нужно, как минимум, затратить энергию W.
Масса ядра может быть определена через массу атома M_ат(A, Z), исходя из значения избытка масс
Δ(A, Z):

M(A, Z)c² = M_ат(A, Z)c² – Zm_ec² = (A·1а.е.м.) + Δ(A, Z) – Zm_ec².

В капельной модели ядра энергия связи ядра описывается формулой Вайцзеккера

W(A,Z) = αА − βA^2/3 − γZ(Z−1)/A^1/3 − δ(A−2Z)²/A + ζA^-3/4.

(9.3)

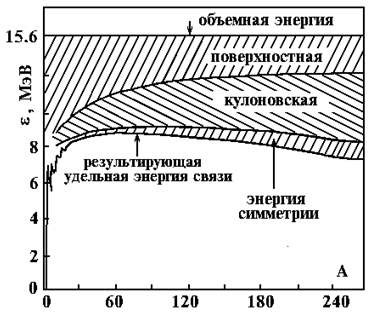
Коэффициенты α, β, γ, δ, ζ подбираются так, чтобы рассчитанные величины энергии связи ядер W максимально близко описывали экспериментально измеренные величины масс атомных ядер M(A,Z). Слагаемые в формуле (9.3) соответствуют различным видам энергии: объемной, поверхностной, кулоновской, энергии симметрии и энергии спаривания. Соответствующие относительные вклады в удельную энергию связи показаны на рис. 9.2.

Рис. 9.2. Вклад различных видов энергии в удельную энергию связи ядра ε(A,Z).

Удельная энергия связи ядра ε(A,Z)

ε(A,Z) = W(A,Z)/A.

(9.4)

Энергия отделения нейтрона

B_n = [М(А-1,Z) + m_n − М(А, Z)]c² = W(А, Z) − W(А-1,Z).

(9.5)

Энергия отделения протона

B_p = [М(А-1,Z-1) + m_p − М(А, Z)]c² = W(А, Z) − W(А-1,Z-1).

(9.6)

Энергия отделения α-частицы

B_α = [M(A-4,Z-2) + m_α − M(A,Z)]c² = W(A,Z) − W(A-4,Z-2) − W(4,2).

(9.7)

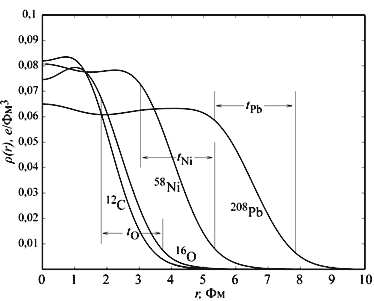
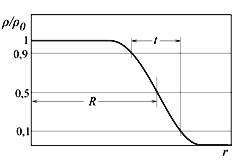
Магические числа

На фоне в целом довольно плавной зависимости энергии связи от массового числа А встречаются ядра, у которых энергия связи больше, чем у соседних ядер. Эти ядра обладают также увеличенной энергией отделения нуклона и повышенной распространенностью в природе. Такие ядра получили название магических, а числа протонов или нейтронов в них – магических чисел. Магические числа следующие:

2, 8, 20, 28, 50, 82, 126.

Существование магических чисел является проявлением оболочечной структуры ядер.

9.3. Радиус атомного ядра

Плотности ρ(r) ядерной материи описывается распределением Ферми

(9.8)

где параметр а связан с толщиной поверхностного слоя t соотношением t ≈ 4.4a и приблизительно равен 0.55 Фм.
Радиус ядра R − расстояние, на котором плотность ядра падает в 2 раза.

R ≈ 1.3×A^1/3 Фм.


	Рис. 9.3. Распределение зарядовой плотности в атомных ядрах, полученное в экспериментах по рассеянию электронов. Толщина поверхностного слоя t = 2.3 Фм.

9.4. Статические характеристики атомных ядер

    Спин атомного ядра. Атомное ядро характеризуется полным моментом количества движения . Эта величина в системе покоя ядра называется спином ядра.
    Четность. Инвариантность системы (гамильтониана ) относительно пространственного отражения – инверсии (замены → -) приводит к закону сохранения чётности и квантовому числу чётность Р.
    Так как внутренние четности протона и нейтрона положительные (+1), четность ядра сферически симметричного ядра может быть представлена как произведение орбитальных четностей нуклонов:

(9.9)

Рис. 9.4.Схема нижних уровней ²⁵Mg (А=25, Z=12).

На схемах ядерных уровней обычно указывают энергию, спин и чётность каждого уровня. Спин указывается числом, а чётность знаком плюс для чётных и минус для нечётных уровней. Этот знак ставится справа сверху от числа, указывающего спин.

Правила для спинов J и чётностей P в основном состоянии ядра:

чётно-чётное ядро	J^P = 0⁺;	(9.10)
нечётное ядро	J = j; P = (-1)^l;
нечётно-нечётное ядро	j_p − j_n\| ≤ J ≤ j_p + j_n;

где j, l, j_p, l_p, j_n, l_n относятся к полному и орбитальному моменту нечётного нуклона (протона, нейтрона).
Изоспин атомного ядра. В ядре A нуклонов, каждый из которых имеет изоспин I = 1/2. Изоспин системы A нуклонов

(9.11)

Все состояния ядра имеют проекцию изоспина I₃ = (Z − N)/2. Поэтому возможны значения изоспина атомного ядра |Z − N|/2 ≤ I ≤A/2. В основном состоянии величина изоспина ядра имеет минимальное значение I = |I₃| = |Z − N|/2.
Магнитный дипольный момент ядра. Атомное ядро, являясь системой движущихся зарядов (токов), обладает магнитным моментом _Я, который имеет орбитальную и спиновую составляющие:

(9.12)

где спиновые и орбитальные гиромагнитные факторы (g-факторы) нуклонов имеют следующие значения:

(9.13)

μ_N − ядерный магнетон, равный eћ/2m_pc = 3.15·10^-18 МэВ/Гс.
Гиромагнитный фактор для ядра g_Я зависит от спина ядра :

_Я = g_Я

(9.14)

Электрический квадрупольный момент ядра. Электрическим квадрупольным моментом ядра считают величину:

(9.15)

где ρ() − зарядовая плотность ядра, а е − величина элементарного электрического заряда. Собственный квадрупольный момент однородно заряженного эллипсоида

Q = (2/5)Z×(b² − a²),

(9.16)

где b и a – длинная и короткая полуоси эллипсоида.
Для оценки степени отклонения формы ядра от сферической обычно вводят параметр деформации β и средний радиус ядра , определяемые соотношениями

= (b + a)/2,

(9.17)

тогда

(9.18)

Обычно для ядер β < 0.6.

9.5. Модель оболочек

В модели оболочек задача многих тел сводится к одночастичной задаче – системе невзаимодействующих нуклонов, находящихся в ядерном потенциале, создаваемом совместным взаимодействием всех нуклонов.
Обычно рассматривают три вида модельного потенциала.
1. Прямоугольная потенциальная яма

V_пя(r) = {	-V₀, r < R	(9.19)
	0, r > R

2. Потенциал гармонического осциллятора

(9.20)

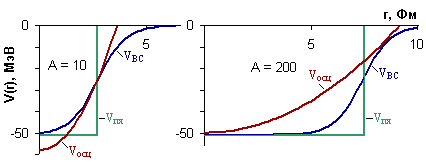
где μ – масса нуклона, а ω – осцилляторная частота.

3. Потенциал Вудса-Саксона

V_В-С(r) = -V₀/[1 + exp(r - R/a)].

(9.21)

Потенциал Вудса-Саксона наиболее близок к реальному ядерному потенциалу.

Рис.1

Рис. 9.5. Осцилляторный потенциал V_осц, прямоугольная потенциальная яма V_пя и потенциал Вудса-Саксона V_ВС. Видно, что в легких ядрах (А = 10) реалистический потенциал лучше воспроизводится осцилляторным, а в тяжелых (А = 200) − прямоугольным.

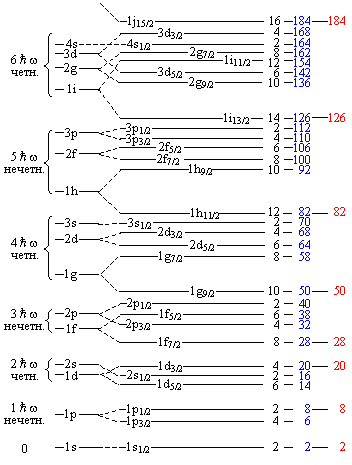
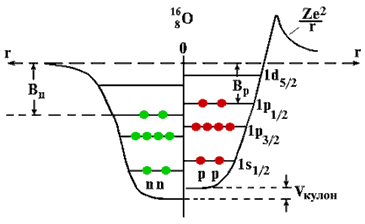
Рис. 9.6. Одночастичные уровни в оболочечном потенциале. Приведено схематическое изображение уровней в потенциале Вудса-Саксона: слева без учета спин-орбитального взаимодействия, справа − с учетом. Фигурные скобки объединяют уровни, входящие в одну осцилляторную оболочку. Черным цветом дано число вакантных мест для нуклонов одного сорта, в синим приведено полное число частиц, красным указаны магические числа

Заполнение ядерных состояний модели оболочек происходит в соответствии с принципом Паули. Состояния нуклона обозначают в виде комбинации числа n (n = 1, 2, … – радиальное квантовое число) и буквы, обозначающей l (l = 1, 2, … – орбитальное квантовое число). Индекс внизу обозначает величину полного момента j = l ±1/2. Одночастичные уровни протонов и нейтронов заселяются независимо, при этом максимальное число нуклонов одного сорта на подоболочке равно числу проекций j на ось z: ν_j = 2j + 1. Состояния ядра определяются расположением нуклонов на одночастичных орбитах и называются конфигурациями. На рис. 9.7 показано распределение нуклонов по подоболочкам в основном состоянии ядра кислорода , отвечающему заполнению самых нижних орбит. Конфигурация ядра в данном случае записывается как:

Нижний индекс у состояния означает тип нуклона, верхний – число нуклонов на подоболочке.

Рис. 9.7 Заполнение подоболочек в основном состоянии ¹⁶O.

Одночастичные состояния в деформированных ядрах.

Одночастичные состояния в деформированных эллипсоидальных ядрах получают, решая уравнение Шредингера для нуклонов, находящихся в потенциальной яме, имеющей форму вытянутого или сплюснутого аксиально симметричного эллипсоида, например в потенциале Нильссона.

(9.22)

Положение одночастичных состояний в потенциале Нильссона зависит от величины и знака параметра деформации β. Связь между частотами ω_xy и ω_z и параметром деформации β

ω_xy = ω₀(1 + β/3), ω_z = ω₀(1 + 2β/3).

Параметры С и D подбираются так, чтобы при β = 0 наилучшим образом описать последовательность уровней сферического оболочечного потенциала

C = -0.1ћω₀, D = -0.02ћω₀.

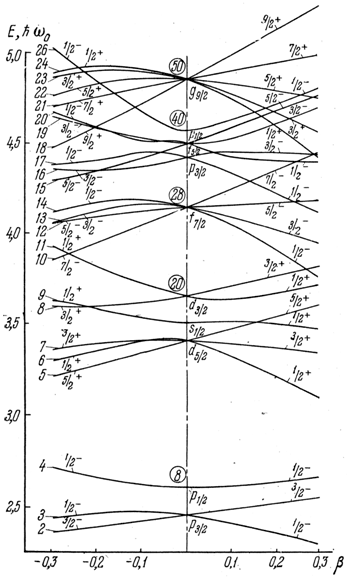
Рис. 9.8. Зависимость положения уровней в нильссоновском самосогласованном потенциале от деформации β. Цифры слева – порядковый номер уровня, цифры в кружке – число частиц при заполнении оболочек в сферически симметричном потенциале вплоть до указанного.

9.6. Возбужденные состояния атомных ядер

Одночастичные возбуждения. В одночастичной модели оболочек возбужденные состояния ядер возникают при переходе одного или нескольких нуклонов на более высокие одночастичные орбиты. Наиболее просто выглядит спектр возбужденных состояний ядер с одним нуклоном или одной «дыркой» сверх заполненных оболочек.

Рис. 9.9. Нижние вращательные уровни ядра ¹⁸⁰Hf. Рядом с экспериментальными значениями энергии приведены энергии, рассчитанные по формуле ћ²J(J+1)/2I с моментом инерции I, оцененным по энергии состояния 2⁺

Вращательные состояния. Характерным признаком вращательных уровней

последовательность значений их спинов-чётностей J^Р = 0⁺, 2⁺, 4⁺, 6⁺, 8⁺, ... для чётно-чётных ядер,
пропорциональность энергии этих уровней величине J(J+1).

E_вращ = ћ²J(J + 1)/(2), (9.23)

где − момент инерции ядра, J - спин ядра, пробегающий   значения 0, 2, 4, .....
    Волновой функцией вращающегося ядра является собственная функция оператора квадрата полного момента ², имеющего собственные значения ћ²J(J+1), т.е. сферическая функция Y_JM(θ,φ). Волновая функция ядра, имеющего форму аксиально-симметричного эллипсоида, не изменяется при отражении в плоскости xy. Поэтому волновая функция такого ядра симметрична, что исключает состояния с J = 1, 3, 5, ... . Чётность сферической функции равна (-1)^J. Поэтому чётность вращательных состояний четно-четного ядра всегда положительна. Примером вращательных уровней являются нижние уровни четно-четного ядра ¹⁸⁰Hf.
     Колебательные состояния сферических ядер. Аналогия между атомным ядром и жидкой каплей поясняет ещё одну форму коллективного движения в атомных ядрах – колебательные состояния. Наиболее низкую частоту имеют квадрупольные колебания, соответствующие полному моменту количества движения J = 2, при которых ядро становится то сплюснутым, что вытянутым эллипсоидом. При октупольных колебаниях J = 3  ядра в деформированном состоянии имеют грушевидную форму.

J = 0 монопольные	J = 1 дипольные	J = 2 квадрупольные	J = 3 октупольные
Рис. 9.10. Примеры колебаний ядра как целого. Сплошной линией показана равновесная (сферическая) форма ядра, а пунктиром - одно из двух крайних (различающихся половиной периода) состояний, которые принимает ядро в процессе колебаний. Дипольные колебания не относятся к внутренним возбуждениям ядра.

Спектры энергий и моментов количества движения возбужденных колебательных состояний дискретны. Энергии квадрупольных и октупольных возбуждений в квантовой теории могут принимать лишь значения

Е_квадр = n₂ћω₂, Е_октуп = n₃ћω₃,

(9.25)

где n₂, n₃ − числа соответственно квадрупольных и октупольных квантов (n₂, n₃, = 1, 2, 3, ...). Для квантов коллективных ядерных колебаний часто используют термин фононы, заимствованный из физики твердого тела.
Каждый квадрупольный квант (фонон) имеет момент количества движения J = 2 и положительную четность. Аналогично, каждый октупольный фонон имеет момент J = 3 и отрицательную четность и т. д. В общем виде энергию возбуждения ядра, в котором одновременно происходят различные поверхностные колебания формы, можно записать в виде

(9.26)

где n_J − число фононов определенного типа, а ћω_J - энергия фонона.
Модель коллективных колебаний хорошо описывает нижние колебательные уровни ядер.

Рис. 9.11. Сравнение спектра низколежащих состояний ядра ¹¹⁴Cd (справа)
с идеальным спектром нижних квадрупольных колебаний поверхности (слева).

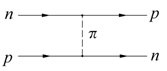
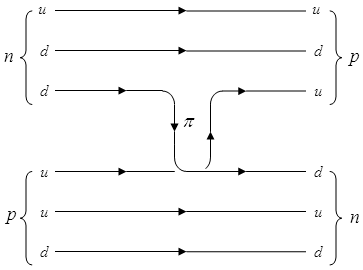
9.7. Мезонная теория ядерных сил

Для описания нуклон-нуклонного взаимодействия Х. Юкава предложил модель, в которой ядерное взаимодействие по аналогии с электромагнитным взаимодействием происходит в результате обмена π-мезоном.


а)	б)
Рис. 9.12 Диаграммы Фейнмана для однопионного np-взаимодействия. a) на нуклонном уровне, б) на кварковом уровне

Обмен скалярными мезонами с нулевым спином J = 0 приводит к притяжению между нуклонами. На меньших расстояниях происходит обмен тяжёлыми мезонами − η (m_ηc² = 549 МэВ),
ρ (m_ρc² = 770 МэВ) и ω (m_ωc² = 782 МэВ). Особую роль в этой области расстояний играет обмен ρ- и ω-мезоном. Характер взаимодействия зависит от спина частицы, переносящей взаимодействие. Обмен векторными мезонами J = 1 приводит к отталкиванию между нуклонами. Это отталкивание является аналогом отталкивания двух одноимённых зарядов в электростатике.

Рис. 9.13. Диаграмма N-N взаимодействий

Потенциал, создаваемый облаком испускаемых нуклоном мезонов, носит название потенциала Юкавы и имеет вид

где а = ћ/mc, m − масса нуклона, g_N − ядерный заряд нуклона.

Задачи

9.1. Вычислить сечение рассеяния α-частицы с кинетической энергией T = 5 МэВ кулоновским полем ядра ²⁰⁸Pb под углами больше 90°.

9.2. При упругом рассеянии электронов с энергией T = 750 МэВ на ядрах ⁴⁰Ca в сечении наблюдается дифракционный минимум под углом θ_min = 18^o. Оценить радиус ядра ⁴⁰Ca.

9.3. Оцените плотность ядерной материи.

9.4. Определите массу ядра ²H (дейтрон) в энергетических единицах, если энергия связи дейтрона
W(2,1) = 2.2 МэВ.

9.5. Масса нейтрального атома ¹⁶O m_ат(A,Z) = 15.9949 а.е.м. Определите удельную энергию связи ε ядра ¹⁶O.

9.6. С помощью формулы Вайцзеккера рассчитайте энергии отделения нейтронов в четно-четных изотопах ³⁸Ca, ⁴⁰Ca, ⁴⁸Ca.

9.7. Считая, что разность энергий связи зеркальных ядер определяется только различием энергий кулоновского отталкивания в этих ядрах, вычислите радиусы зеркальных ядер ²³Na, ²³Mg. W(²³Na) = 186.56 МэВ, W(²³Mg) = 181.72 МэВ.

9.8. Определите значения изоспинов I основных состояний изотопов углерода ¹⁰C, ¹¹C, ¹²C, ¹³C, ¹⁴C.

9.9. Рассчитайте расстояние между уровнями 1s, 2s и 3s ядра ⁹⁰Zr в случае прямоугольной потенциальной ямы бесконечной глубины и ямы гармонического осциллятора

V(r) = -V₀ + mω²r²/2 при V₀ = 40 МэВ.

9.10. На схеме показан спектр возбужденных состояний ядра ¹⁰⁶Pd. Оценить энергию первого возбужденного состояния 2⁺.

9.11. Среднее расстояние между нуклонами в ядре ~1.7 Фм. Считая протоны точечными частицами, оцените энергии кулоновского V_кул и ядерного (нуклон-нуклонного) взаимодействий V_NN двух протонов, находящихся на расстоянии 2 Фм.

9.12. Покажите, что из определённой чётности волновой функции ядра следует равенство нулю его электрического дипольного момента.

9.13. Параметр деформации β ядра ¹⁷⁶Lu равен +0.31. Рассчитайте отношение полуосей b и a ядерного эллипсоида. Опишите его форму и вычислите собственный квадрупольный момент ядра Q₀.

9.14. Получите формулу для рассеяния Резерфорда в диапазоне углов θ₁ < θ < θ₂:

где R₀ = zZe²/T – радиус наименьшего сближения ядер при кулоновском рассеянии.

9.15. Вычислите сечение рассеяния α-частицы с кинетической энергией T = 8 МэВ кулоновским полем ядра кальция ⁴⁸Ca под углами больше 120º.
Ответ: σ(θ > 120^o) = 13.5 фм² = 0.14 барн

9.16. Пучок α-частиц с кинетической энергией T = 5 МэВ падает на тонкую алюминиевую фольгу. Каково отношение числа частиц, зарегистрированных в диапазоне углов от 30º до 60º к числу частиц в диапазоне от 120º до 150º?
Ответ: N(30^o –60^o)/N(120^o – 150^o) = 41.75

9.17. Пучок протонов (поток J = 3.6·10⁴ c^–1) с энергией 500 кэВ падает на золотую фольгу толщиной 1·10¹⁹ ядер/cм².
1)    Рассчитайте число частиц, рассеянных в заднюю полусферу (θ > 90º) за две минуты облучения.
2)    Рассчитайте сечение рассеяния в диапазоне углов от 59º до 61º.
3)    Определите число частиц, рассеиваемых ежесекундно под углами меньше 30º
Ответ: 1) ∆N = 17 514 частиц, 2) σ = 516 барн, 3) N = 2.8·10⁴ с^–1

9.18. При рассеянии электронов с энергией T = 500 МэВ на ядрах свинца ²⁰⁸Pb первый дифракционный минимум в сечении наблюдается под углом θ = 10º. Оцените радиус ядра свинца. Сравните результат с оценкой по приближенной формуле R = r₀A^1/3.
Ответ: R = 8 Фм

9.19. Перечислите магические числа. Объясните причину появления магических чисел. Перечислите дважды магические ядра. Могут ли быть магические числа в деформированных ядрах?

9.20. Масса переносчика ядерного взаимодействия π-мезона m_πc² ≈ 140 МэВ. Определить радиус действия ядерных сил r_NN.
Ответ: r_NN ≈ 1.4 Фм

9.21. В чем различие ядерных и электромагнитных сил? Что между ними общего?

9.22. Спин ядра ⁶Li в основном состоянии равен J = 1. Покажите, что это значение спина ядра несовместимо с представлением, что атомное ядро состоит из протонов и электронов.

9.23. Магнитные моменты дейтрона ²H и ядра фтора ¹⁷F равны соответственно 0.86μ_N и 4.77μ_N. Покажите, что эти значения магнитных моментов ядер несовместимы с протон-электронной моделью ядра.

9.24. Используя формулу Вайцзеккера, вычислите энергию связи и массы ядер ¹⁶O, ⁵⁶Fe, ²⁰⁸Pb, ²³⁸U. Рассчитайте вклады объемной, поверхностной и кулоновской энергий. Сравните полученные значения удельной энергии связи с табличными значениями.

9.25. Вычислите радиусы ядер 1) ¹⁶O, ¹⁹⁷Au, ²³⁵U; 2) ¹²C, ⁵⁶Fe, ²⁰⁸Pb.

9.26. Какую энергию надо затратить, чтобы удалить а) нейтрон, б) протон, в) α- частицу из следующих ядер: 1) кислорода ¹⁶O, 2) азота ¹⁴N, 3) кальция ⁴⁰Ca, 4) железа ⁵⁶Fe, 5) стронция ⁶⁷Sr, 6) урана ²³⁸U?

9.27. Используя оболочечную модель ядра, выпишите конфигурацию и определите орбитальный момент l, полный момент J, четность Р и изоспин I следующих ядерЮ находящихся в основном состоянии: 1) ⁵He, ¹³C, ¹⁵O, ¹⁷F; 2) ⁷Li, ¹¹C, ¹⁴C, ²⁷Al; 3) ⁴¹Ca, ⁴³Ca, ⁴⁸Ca, ⁷³Ge; 4) ³³S, ³⁹K, ⁶³Cu, ¹²⁵Sn;
5) ¹⁶O, ¹⁷O, ¹⁸O, ²⁹Si; 6) ²⁰⁷Pb, ²⁰⁸Pb, ²⁰⁹Pb, ²⁰⁹Bi. Сравните полученные значения с табличными.

9.28. Определите спин и четность α-частицы. Запишите ее конфигурацию. Исходя из табличных данных по избыткам масс, вычислите энергию связи α-частицы.
Ответ: ⁴He: J^P = 0⁺; |1s_1/2>⁴

9.29. Каким изотопам соответствуют следующие конфигурации

1)         2)
3)           4)
5)                        6)
7)           8)
9)                     10)
Определите спин, четность и изоспин указанных ядер
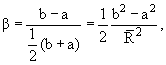
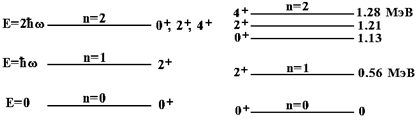
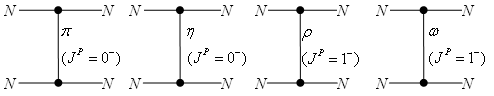
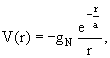
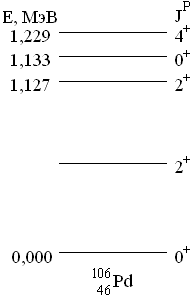
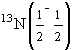Ответ: ^AX(J^PI): 1) ¹⁰C(0⁺1), 2) , 3)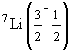, 4) ²⁰O(0⁺2), 5)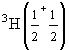, 6) ²⁸Si(0⁺0),
7), 8)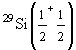, 9) ⁶H(0⁺1), 10)

9.30. Определить спин основного состояния I и проекцию изоспина I_z ядер ⁷Be, ¹⁴O, ¹⁴C, ²⁸Si, ⁷Li, ¹⁴N. Укажите изотопический синглет, дублет и триплет, сформированные из данных ядер. Какие из этих состояний соответствуют основным состояниям? Что можно сказать о спине и четности состояний ядра ¹⁴N, входящего в соответствующий изоспиновый мультиплет?
Ответ: Синглет (I = 0) ²⁸Si; дублет (I = 1/2) ⁷Li, ⁷Be; триплет (I = 1) ¹⁴С, ¹⁴N^*, ¹⁴O

9.31. Вычислите разности энергий связи в парах зеркальных ядер 1) ⁷Li–⁷Be, 2) ¹¹B–¹¹C, 3) ¹⁵O–¹⁵N. Сравните полученный результат с энергией электростатического отталкивания протонов в этих ядрах.
Ответ: 1) ∆U_Coul = 2.4 МэВ, ∆ε = 1.6 МэВ; 2) ∆U_Coul = 3.3 МэВ, ∆ε = 2.8 МэВ; 3) ∆U_Coul= 4.0 МэВ,
∆ε = 3.5 МэВ

9.32. Продифференцируйте формулу Вайцзеккера и получите связь между A и Z для стабильных изотопов.

9.33. Исходя из табличных данных по избыткам масс, вычислите энергию связи дейтрона.

9.34. Исходя из табличных данных по избыткам масс, рассчитайте энергии отделения протонов и нейтронов
1)    В изотопах кремния Si с массовыми числами A от 24 до 42;
2)    В изотопах кальция Ca с массовыми числами A от 36 до 54;
3)    В изотопах олова Sn с массовыми числами A от 98 до 136;
Постройте зависимость этих величин от массового числа A и объясните ее основные особенности.

9.35. Используя величины масс атомных ядер, рассчитайте зависимость энергии отделения двух нейтронов от массового числа A для четно-четных изотопов 1) Ca (Z = 20), 2) Sn (Z = 50),
3) Pb (Z = 82). Объясните полученную зависимость.

9.33-35. Проверить результаты можно по базам ядерных данных

9.36. Покажите, что для однородной сферически симметричной системы зарядов (например, сферически симметричного ядра) собственный (внутренний) электрический квадрупольный момент Q₀= 0.

9.37. Покажите, что квадрупольный момент равномерно заряженного эллипсоида с полуосями a и b определяется выражением Q = 2Ze(a² − b²)/5.

9.38. Покажите, что спектр возбужденных состояний деформированного ядра ¹⁸⁰Hf представляет собой «вращательную полосу».

9.39. Значения энергий возбужденных состояний ядра диспрозия ¹⁶⁰Dy: E(2⁺) = 87 кэВ,
E(4⁺) = 284 кэВ, E(6⁺) = 582 кэВ, E(8⁺) = 972 кэВ, E(10⁺) = 1442 кэВ. Покажите, что спектр возбужденных состояний деформированного ядра диспрозия ¹⁶⁰Dy представляет собой «вращательную полосу».

27.10.2016