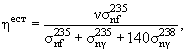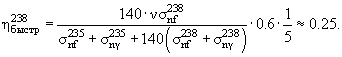Семинар 12. Деление ядерНа устойчивость атомного ядра влияют два типа сил:
С увеличением массы и размера ядра кулоновское отталкивание приводит к уникальному явлению – ядро может разделиться на два сравнимых по массе осколка. Неустойчивость атомного ядра по отношению к делению описывается параметром делимости Z2/А.
12.1. Деление атомных ядерДелением атомных ядер называют их распад на два осколка сравнимой массы. Деление может быть самопроизвольным (спонтанным) или вынужденным, вызванным взаимодействием с налетающей частицей. Характеристики распадов некоторых ядер
Деление энергетически выгодно для тяжёлых ядер и является основным источником ядерной энергии. При этом энерговыделение составляет величину ≈1 МэВ на один нуклон делящегося вещества или 1014 Дж/кг, что на много порядков превосходит энерговыделение всех других освоенных человеком источников энергии. 12.2. Энергия деления При делении тяжёлых ядер выделяется энергия, что следует
из зависимости удельной энергии связи ε = W(A, Z)/А
от массового числа A. При
делении тяжёлого ядра образуются более лёгкие ядра, в которых нуклоны связаны
сильнее, и часть энергии высвобождается. Едел = 2W(A/2, Z/2) −
W(A,Z) ≈ Деление энергетически выгодно (Eдел > 0) в том случае, когда (0.37γZ2/A1/3 − 0.26βA2/3) > 0, т. е. когда
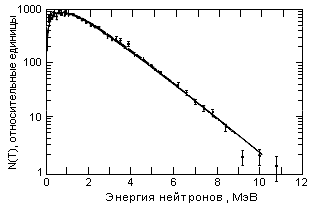
Величина Z2/A называется параметром делимости. Z2/A > 17 для ядер с А > 90. 12.3. Продукты деленияРаспределение энергии деления 235U тепловыми нейтронами
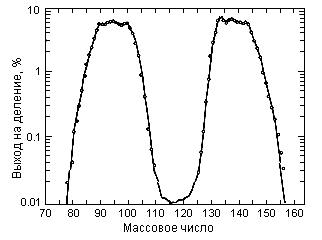
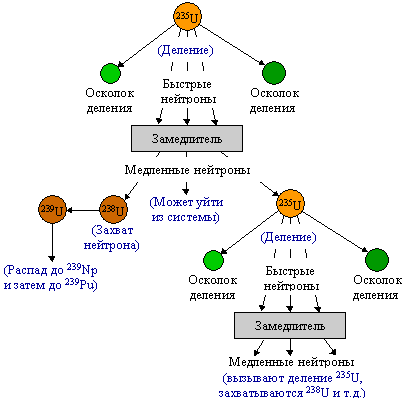
Характерной особенностью деления изотопов урана является то, что осколки, как правило, существенно различаются по массам, т. е. преобладает асимметричное деление. С учётом испускания двух мгновенных нейтронов, один из каналов реакции деления 235U имеет вид n + 235U → 236U → 95Sr + 139Xe + 2n. Распределение по массам осколков деления
показано на
рис. 12.1. Осколки деления
образуются в широком диапазоне A
= 72–161 и Z = 30–65. Осколки деления в момент образования сильно перегружены нейтронами и испытывают последовательный β--распад, причем заряд первичного осколка может увеличиваться на 4–6 единиц.
Восстановление характерного для средних ядер
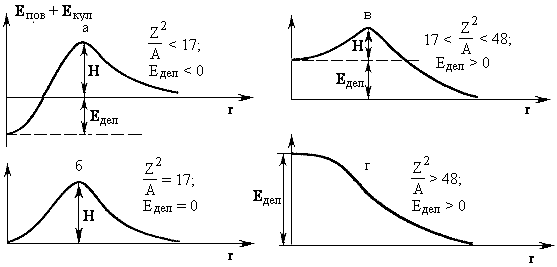
12.4. Механизм деленияПоверхностная и кулоновская энергии изменяются при отклонениях формы исходного ядра от сферической. Если ядро принимает форму вытянутого эллипсоида вращения, то при условии, что объём ядра не изменяется (ядерная материя практически несжимаема), величины малой a и большой b осей ядерного эллипсоида:
где R −
радиус исходного ядра, а ε − малый
параметр.
Изменение полной энергии ядра при переходе от сферической формы к эллипсоиду определяется соотношением
Барьер деления возникает при ΔE > 0, т. е. при Z2/А
< 2β/γ ≈ 48.
12.5. Деление естественной смеси изотопов UВ естественной смеси изотопов U на тепловых нейтронах реакция возможна, а на быстрых − нет. Среднее число вторичных нейтронов на один захват нейтрона естественной смесью изотопов урана
где ν – среднее число нейтронов, испускаемых в одном акте деления, σnf , σnγ – сечения реакций деления (n,f) и радиационного захвата (n,γ).
Следовательно, цепная реакция на тепловых нейтронах на естественном уране возможна. Однако для осуществления цепной реакции надо с малыми потерями замедлять образующиеся при делении нейтроны с энергией от несколько МэВ до тепловых.
Необходимо учесть, что быстрые нейтроны с энергиями больше 1.4 МэВ
могут с заметной относительной интенсивностью делить и ядра изотопа
238U,
которого в естественной смеси гораздо больше. При делении 238U коэффициент
ν ≈ 2.5.
В спектре деления 60% нейтронов имеют энергии выше эффективного порога
1.4 МэВ деления 238U.
Из этих 60% нейтронов только один нейтрон из пяти успевает вызвать
деление 238U,
не замедлившись до энергии ниже пороговой за счет упругого и неупругого
рассеяния. Для быстрых нейтронов
Полный коэффициент
На быстрых нейтронах цепная реакция в естественной смеси изотопов 235U и 238U идти не может. Реакцию на быстрых нейтронах можно поддерживать лишь в обогащенной смеси, содержащей не меньше 15% изотопа 235U. 12.6. Цепная реакция деленияЦепная реакция деления идет в среде, в которой происходит процесс размножения нейтронов. Такая среда называется активной средой. Физической величиной, характеризующей интенсивность размножения нейтронов, является коэффициент размножения нейтронов k∞, равный отношению количества нейтронов в одном поколении к их количеству в предыдущем поколении. Индекс ∞ относится к среде бесконечных размеров. В делящейся среде конечных размеров часть нейтронов будет уходить из активной зоны наружу. Поэтому коэффициент k, являющийся характеристикой конкретной установки, зависит от вероятности Р для нейтрона не уйти из активной зоны. По определению k = k∞·P. Величина Р зависит от состава активной зоны, ее
размеров, формы, а также от того, в какой степени вещество, окружающее
активную зону, отражает нейтроны.
12.7. Ядерный реактор
В реакторе поддерживается
управляемая цепная реакция деления, в результате которой происходит выделение
тепла. Основной характеристикой реактора является его мощность − количество
тепловой энергии, выделяющейся в единицу времени. Мощность в 1 МВт (мегаватт)
соответствует цепной реакции, в которой происходит 3·1016 актов
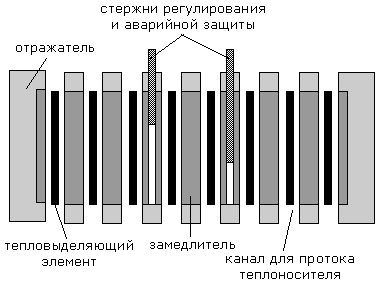
деления в секунду. Имеется большое количество разных типов реакторов. Одна из
типичных схем теплового реактора изображена на рисунке 12.5.
Эти две реакции открывают возможность воспроизводства ядерного горючего в процессе цепной реакции. 12.8. Ядерный взрыв
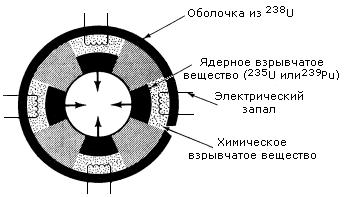
Ядерный взрыв развивается за счёт экспоненциально растущего со временем числа разделившихся ядер: N(t) = N0et/τ. Среднее время τ между двумя последовательными актами
деления 10-8 с. Отсюда можно получить для времени полного деления 1
кг ядерной взрывчатки величину
|
|||||||||||||||||||||||||||||||||||||||||||||||
.
b = R(1 + ε),
=
580 барн,
=
112 барн,
=
2.8 барн. 
=
1.32 > 1.
≈
0.033.
≈ 0.6 барн
и для коэффициента
получается
оценка
для
реакции деления на быстрых нейтронах в естественной смеси изотопов урана
равен сумме
.
Рассчитайте энергию электростатического отталкивания осколков EКулон.
Сравните полученный результат с суммарной кинетической энергией осколков равной
≈ 170 МэВ.
