Семинар 14.
Симметрии Природы
Симметрии являются одним из
фундаментальных принципов построения физических теорий. Обнаружение общих
закономерностей между различными явлениями природы приводит к объединению,
казалось бы, совершенно непохожих взаимодействий. Так возникло гравитационное
взаимодействие, описывающее с единых позиций притяжение массивных тел на Земле и
столкновение галактик в космосе. Электромагнитное взаимодействие объединило
такие явления как взаимодействие магнитов, заряженных тел и возникновение света.
Объединение четырех фундаментальных взаимодействий является одной из ключевых
задач физики.
14.1.
Операции симметрии
14.2. Изоспиновая симметрия
14.3. Симметрии протранства-времени
14.4. Законы сохранения
14.5. Комбинированная четность. СР-четность
14.6. Распады нейтральных каонов
14.7. Теорема СРТ
14.8. Обращение времени
14.9. Объединение взаимодействий
14.10. Распад протона
14.11. Суперсимметрия
Задачи
14.1. Оператор симметрии
Система
обладает симметрией относительно преобразования U, если
состояние системы не изменяется в результате применения к ней этого
преобразования.
Оператор
U переводит волновую функцию
ψ(r,t) в другую волновую функцию
ψ'(r,t) = Uψ(r,t). Симметрия системы
определяется симметрией гамильтониана, описывающего данную систему. Оператор
U называется оператором симметрии, если
Uψ удовлетворяет тому же самому
уравнению Шредингера, что и функция
ψ.
HU − UH ≡ [H,U] = 0.
Оператор симметрии
U должен коммутировать с гамильтонианом
H.
14.2. Изоспиновая симметрия
Изоспиновая симметрия − это
симметрия сильных взаимодействий, в основе которой лежит представление о том,
что u- и d-кварки являются
одинаковыми частицами по отношению к сильному взаимодействию, имеющими значение
изоспина I = 1/2 и различающимися знаком проекции
вектора изоспина I3 на ось 3 декартового зарядового пространства.
u(I = 1/2, I3 = +1/2)
d(I = 1/2, I3 = -1/2)
Кварковые системы, обладающие
определенным значением изоспина, вырождены по знаку проекции изоспина.
Число частиц N
в изотопическом мультиплете
N = 2I +1.
В барионный
декуплет входят нуклонные резонансы, имеющие значение JP = 3/2+. Одинаковая разность
масс между состояниями с различными значениями I определяется числом s‑кварков,
образующих состояния с определенным значением изоспина I.
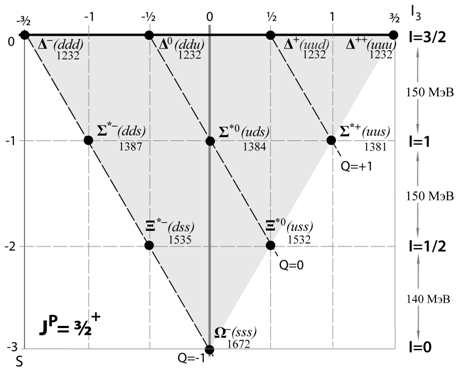
Рис. 14.1. Барионный декуплет со спином JP = 3/2+.
14.3. Симметрии пространства-времени
- Симметрия физических
законов относительно сдвигов в пространстве означает эквивалентность всех точек
пространства − однородность пространства. С однородностью пространства связан
закон сохранения импульса
 . .
- Симметрия физических
законов относительно поворотов системы как целого в пространстве означает
эквивалентность всех направлений в пространстве, т.е. оно изотропно. С
изотропностью физического пространства связан закон сохранения момента
количества движения J.
- Симметрия физических
законов относительно начала отсчета времени (сдвиг во времени) означает
эквивалентность всех моментов времени. Время однородно, т.е. физические законы
не меняются с течением времени. С однородностью времени связан закон сохранения
энергии Е.
- Симметрия физических
законов относительно всех систем отсчета Х, движущихся друг относительно друга с
постоянной по величине и направлению скоростью, означает эквивалентность всех
инерциальных систем отсчета.
- Выполнение законов
сохранения энергии E, импульса
 , момента количества движения J обусловлено макроскопической структурой пространства-времени
на больших расстояниях. , момента количества движения J обусловлено макроскопической структурой пространства-времени
на больших расстояниях.
- Понятие симметрии можно
расширить, включив в него более абстрактные понятия.
14.4. Законы сохранения
| Аддитивные законы
сохранения |
| Характеристика |
Взаимодействие |
Сильное |
Электромагнитное |
Слабое |
Электрический заряд, Q |
+ |
+ |
+ |
Энергия, E |
+ |
+ |
+ |
Импульс, p |
+ |
+ |
+ |
Угловой момент, J |
+ |
+ |
+ |
Барионный заряд, B |
+ |
+ |
+ |
Лептонные заряды, Le, Lμ, Lτ |
+ |
+ |
+ |
Странность, s |
+ |
+ |
− |
Charm, c |
+ |
+ |
− |
Bottom, b |
+ |
+ |
− |
Top, t |
+ |
+ |
− |
Изоспин, I |
+ |
− |
− |
Проекция изоспина, I3 |
+ |
+ |
− |
Дискретные симметрии
Ряд законов сохранения связан с
различными операциями отражения. Операции отражения имеют два общих свойства.
- Отражение является
дискретной операцией.
- Если провести операцию
отражения два раза подряд, то в результате система возвратится в исходное
состояние.
Мультипликативные
законы сохранения |
| Характеристика |
Взаимодействие |
| Сильное |
Электромагнитное |
Слабое |
Пространственная
четность, P |
+ |
+ |
− |
Зарядовая четность, C |
+ |
+ |
− |
Временная четность, T |
+ |
+ |
− |
Комбинированная
четность, CP |
+ |
+ |
− |
CPT-четность |
+ |
+ |
+ |
G-четность |
+ |
− |
− |
Наиболее привычным примером
операции отражения является зеркальное отражение относительно какой-либо
плоскости.
Оператор пространственной
инверсии меняет знак пространственных координат
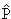 ( ( )
= - )
= - : :
x, y, z,
 , ,

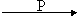 -x,
-y, -z, - -x,
-y, -z, - , ,
 . .
Оператор зарядового сопряжения
меняет знак всех аддитивных квантовых чисел (зарядов) частиц, тем самым переводя
частицу в античастицу
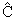 (A) =
A. (A) =
A.
14.5. Комбинированная четность. СР-четность
Операция СР сопряжения состоит в
проведении С и Р преобразований в любой последовательности. На рис. 14.2
показана операция СР-сопряжения слабого распада π+-мезона для
последовательного Р и С преобразования (слева) и последовательного С и Р
преобразования (справа). В результате СР-преобразования получается процесс,
наблюдаемый в природе – распад π–-мезона.
СР четность не сохраняется в распадах нейтральных K, D, B
и Bs мезонов
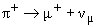 |
|
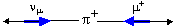 |
|
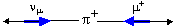 |
|
P |
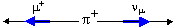 |
C |
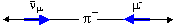 |
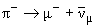 |
PC |
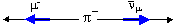 |
CP |
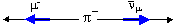 |
|
Рис.
14.2 СР-сопряжение слабого распада π+-мезона
в PC (слева) и CP
(справа) последовательности. Черными стрелками показано направление
импульсов частиц, синие стрелки обозначают направление спинов
частиц. |
14.6. Распады
нейтральных каонов
Нейтральные К0-мезоны:
К0(d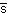 ),
K0( ),
K0(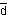 s). s).
Исследование процессов с участием
нейтральных К0 и
K0-мезонов позволяет изучить проявление принципа
суперпозиции в квантовой механике.
- Линейная комбинация двух
состояний также является состоянием системы.
К0 и
K0-мезоны можно представить
как суперпозицию двух других состояний
K1 и
K2.
- В слабых распадах
К0 и
K0-мезонов впервые было обнаружено, что
CP-симметрия не является точной симметрией.
Образование K0-мезонов
К0(d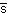 )JP(I)
= 0−(1/2),
K0( )JP(I)
= 0−(1/2),
K0(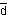 s)JP(I)
= 0−(1/2). s)JP(I)
= 0−(1/2).
Нейтральные мезоны
К0 и
K0 являются частицей и
античастицей и различаются квантовыми числами странность и проекция изоспина
s(К0) = +1, s(K0)
= -1; I3(К0) = -1/2, I3(K0)
= +1/2.
Поэтому обе
частицы должны иметь одинаковые массы и одинаковые времена жизни. Они по-разному
ведут себя в сильном взаимодействии.
К0-мезоны могут образовываться в
реакции
π− + p → Λ + К0, Δs = 0,
в то время, как для
K0-мезонов такая реакция
запрещена
π− + p
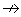 Λ +
K0, Δs
= 2. Λ +
K0, Δs
= 2.
K0-мезоны в сильных
взаимодействиях образуются в реакции
π− + p → Λ +
K0
+ К0, Δs = 0,
которая имеет более высокий порог.
Переходы
К0-K0
Каоны
К0 и
K0 являются частицей и
античастицей по отношению друг к другу и связаны операцией зарядового
сопряжения, причем фазы преобразования выбраны так, чтобы
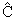 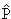 |К0> = |K0>,
|К0> = |K0>,
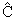 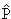 |K0>
= |К0>.
|K0>
= |К0>.
Нейтральные
каоны рождаются в сохраняющем изоспин и странность сильном взаимодействии, а
распадаются в результате слабого взаимодействия на два или три пионы. В слабом
взаимодействии странность может не сохраняться. Находясь в свободном состоянии,
К0- и
K0-мезоны могут переходить друг
в друга в результате двух последовательных виртуальных процессов с изменением
странности в каждом из них на единицу Δs = 1.
В результате
возникает смешивание состояний
К0 и
K0. Механизм этого смешивания можно
описать с помощью кварковой диаграммы:
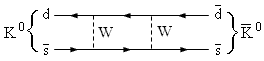
В результате этого смешивания
возникают линейные комбинации:
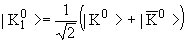 , ,
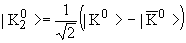 . .
Состояния
|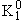 > и
| > и
|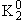 > имеют определенные значения CP‑четности, но не имеют определенного значения странности
s. > имеют определенные значения CP‑четности, но не имеют определенного значения странности
s.
В свою очередь
К0 и
K0 являются суперпозицией
состояний
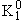 и и
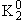 . .
|К0> = (|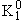 >
+ | >
+ |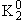 >)/ >)/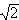 , ,
|K0> = (|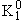 > − | > − |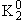 >)/ >)/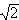 . .
CP(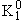 )
= +1, и в соответствии с законом сохранения
комбинированной четности )
= +1, и в соответствии с законом сохранения
комбинированной четности
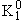 распадается на два π-мезона. Среднее время жизни состояния
τ( распадается на два π-мезона. Среднее время жизни состояния
τ(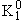 ) ≈
0.9·10-10 с. Это сравнительно короткоживущее состояние
обозначают ) ≈
0.9·10-10 с. Это сравнительно короткоживущее состояние
обозначают
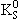 (short). (short).
CP(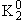 )
= -1 , поэтому при сохранении комбинированной четности )
= -1 , поэтому при сохранении комбинированной четности
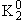 распадается на 3
π-мезона. Время жизни распадается на 3
π-мезона. Время жизни
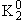 должно быть больше времени жизни должно быть больше времени жизни
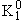 τ( τ(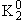 ) ~ 5·10-8
с из-за существенного различия в энергии реакции (Q1 −
Q2 = mπ). Это сравнительно долгоживущее состояние обозначают ) ~ 5·10-8
с из-за существенного различия в энергии реакции (Q1 −
Q2 = mπ). Это сравнительно долгоживущее состояние обозначают
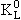 (long). (long).
Так как
K0-мезон на 50% состоит из компоненты
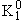 , то вблизи мишени наблюдаются
распады этой компоненты на 2 π-мезона. На большем
расстоянии от мишени наблюдается распад компоненты , то вблизи мишени наблюдаются
распады этой компоненты на 2 π-мезона. На большем
расстоянии от мишени наблюдается распад компоненты
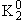 на 3 π-мезона. на 3 π-мезона.
Распады
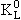 на 2π-мезона
на 2π-мезона
Однако, в 1964
г. Дж. Кронин и
В.Фитч обнаружили, что в распадах нейтральных каонов происходит
нарушение СР‑инвариантности. Существует малая, но конечная вероятность распада:
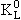 → π+
+ π−, → π+
+ π−,
в котором собственное значение
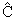 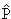 -оператора в конечном состоянии имеет СР = +1: -оператора в конечном состоянии имеет СР = +1:
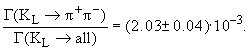
Этот результат означает, что
нельзя отождествлять состояние
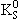 с с 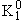 и и
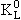 с с
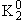 . Cостояния . Cостояния
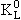 и и
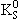 нужно определить следующим образом: нужно определить следующим образом:
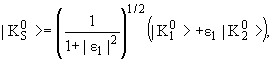
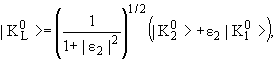
ε1 и ε2 − малые комплексные числа.
14.7. СРТ теорема
Г. Людерсом и
В. Паули была доказана
фундаментальная теорема.
Квантовые системы
инвариантны относительно СРТ-преобразования в любой последовательности.
Следствием СРТ-инвариантности является равенство масс и времен жизни
частицы и античастицы.
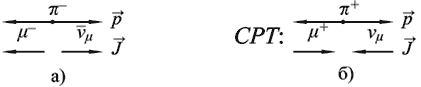
Рис. 14.3. Распад π−-мезона (а) и СРТ-преобразование для распада (б).
В силу СРТ-инвариантности, если в природе происходит некоторый процесс, то точно
с такой же вероятностью может происходить СРТ‑сопряженный процесс, в котором
частицы заменены соответствующими античастицами, проекции их спинов и импульсов
изменили знак, а начальное и конечное состояния поменялись местами. Вероятности
распадов π– → μ− +  μ и
π+ → μ+ + νμ одинаковы. На опыте не
обнаружено ни одного случая нарушения СРТ‑инвариантности. μ и
π+ → μ+ + νμ одинаковы. На опыте не
обнаружено ни одного случая нарушения СРТ‑инвариантности.
Сохранение СРТ-симметрии следует из самых общих принципов квантовой физики. Если
СРТ-симметрия сохраняется, то из несохранения СР‑симметрии следует несохранение
T-симметрии.
14.8. Обращение времени
Операция
обращения времени Т сводится к замене
t → -t. Преобразование
пространственных координат
 , импульса , импульса
 и момента импульса и момента импульса
 при операции обращения времени: при операции обращения времени:
 , ,
 , ,
 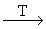  ,
- ,
- , - , - . .
В результате
Т-преобразования происходит изменение знаков импульса, момента импульса и
меняются местами начальное и конечное состояния. Операция обращения времени
превращает исходное движение в обратное.

Рис. 14.4 Распад
π−-мезона (а) и Т-преобразование для распада (б).
Из требования Т-инвариантности следует равенство сечений прямого и обратного
процессов.
Из Т-симметрии
следует соотношение между сечениями прямых и обратных реакций (принцип обратного
равновесия), что позволяет проверить выполнение Т-инвариантности в различных процессах.
14.9. Объединение взаимодействий
Современные
идеи объединения различных взаимодействий берут начало от работ Ньютона. Ньютон
открыл простой закон, согласно которому сила взаимодействия между двумя
массивными телами пропорциональна их массам m1 , m2 и обратно пропорциональна квадрату расстояния
r между ними:
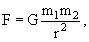
G −
гравитационная постоянная Ньютона.
С помощью этого
закона Ньютон сумел рассчитать как закономерности падения тел, согласующиеся с
наблюдениями Галилея, так и закономерности движения планет, ранее
установленные Кеплером. С помощью одного закона впервые удалось описать явления
земных и космических масштабов.
Следующий шаг в
объединении взаимодействий был сделан Максвеллом, который показал, что
электричество, магнетизм и свет можно описать системой дифференциальных
уравнений, которые носят его имя.
В картине
объединения взаимодействий различают три порога.
Первый − 100
ГэВ − это порог электрослабого взаимодействия, который соответствует массе
W и Z-бозонов. При этих энергиях происходит объединение
электромагнитного и слабого взаимодействий.
Второй −
~1015 ГэВ. Это характерная величина энергии, при которой происходит объединение
сильного и электрослабого взаимодействий. Такой массой должны обладать
X- и Y-бозоны, обеспечивающие симметрию кварков и лептонов.
X- и Y-бозоны могут превращать кварки в лептоны и лептоны — в
кварки.
Третий − ~ 1019 ГэВ − это энергия Планка. При этих энергиях в единое
взаимодействие объединяются все известные взаимодействия, включая
гравитационное.
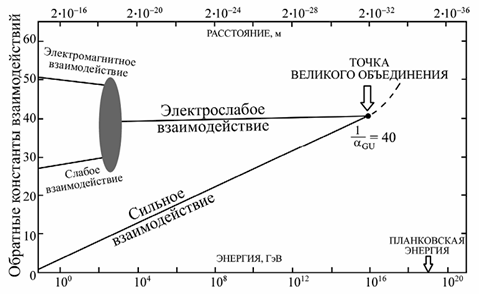 При уменьшении
расстояния или, что эквивалентно, при увеличении энергии константа
электромагнитного взаимодействия возрастает, в то время как константы сильного
и слабого взаимодействия уменьшаются. Расчеты показывают, что если учесть
влияние квантовых флуктуаций, константы взаимодействий начнут сближаться, и
станут практически одинаковыми на расстоянии ~10-29 см.
Температура и энергия, соответствующие таким масштабам составляют 1028 К и
E = 1016 ГэВ. Такие характеристики
имела Вселенная, когда её возраст составлял 10-39 с.
14.10. Распад
протона
Одним из
важнейших предсказаний ТВО является распад протона. За возможные распады протона
отвечают процессы с участием X- и Y‑бозонов.
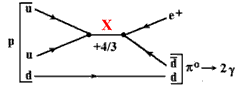
Вероятность распада протона чрезвычайно мала из-за большой массы X- и
Y‑бозонов. По оценкам время жизни протона относительно доминирующего канала
распада p → e+ + π0 не может превышать 1032 лет. Для этого канала распада
протона эксперимент уже даёт t > 5·1032 лет.
 |
p → e+ + π0 |
↓
2γ |
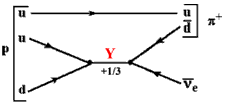 |
p →
 e + π+ e + π+ |
14.11. Суперсимметрия
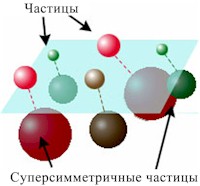 Предположение о существовании симметрии законов природы, связанной со спином,
приводит к понятию суперсимметрии – симметрии между частицами с полуцелым спином
(фермионы – кварки, лептоны) и частицами с целым спином (бозоны – фотон, глюоны,
W, Z…). Каждой известной частице должен соответствовать суперсимметричный
партнер, спин которого отличается на 1/2. Массы суперпартнеров должны быть
гораздо больше, чем у наблюдаемых сейчас
Предположение о существовании симметрии законов природы, связанной со спином,
приводит к понятию суперсимметрии – симметрии между частицами с полуцелым спином
(фермионы – кварки, лептоны) и частицами с целым спином (бозоны – фотон, глюоны,
W, Z…). Каждой известной частице должен соответствовать суперсимметричный
партнер, спин которого отличается на 1/2. Массы суперпартнеров должны быть
гораздо больше, чем у наблюдаемых сейчас
| Частица |
Спин |
SUSY-партнёр |
Спин |
| кварк |
1/2 |
скварк |
0 |
| лептон |
1/2 |
слептон |
0 |
| нейтрино |
1/2 |
снейтрино |
0 |
| фотон |
1 |
фотино |
1/2 |
| глюон |
1 |
глюино |
1/2 |
| W-бозон |
1 |
вино |
1/2 |
| Z-бозон |
1 |
зино |
1/2 |
| хиггс |
0 |
хиггсино |
1/2 |
| гравитон |
2 |
гравитино |
3/2 |
|


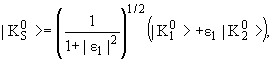
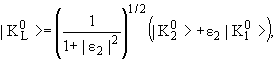
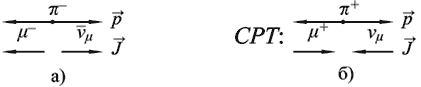




 Предположение о существовании симметрии законов природы, связанной со спином,
приводит к понятию суперсимметрии – симметрии между частицами с полуцелым спином
(фермионы – кварки, лептоны) и частицами с целым спином (бозоны – фотон, глюоны,
W, Z…). Каждой известной частице должен соответствовать суперсимметричный
партнер, спин которого отличается на 1/2. Массы суперпартнеров должны быть
гораздо больше, чем у наблюдаемых сейчас
Предположение о существовании симметрии законов природы, связанной со спином,
приводит к понятию суперсимметрии – симметрии между частицами с полуцелым спином
(фермионы – кварки, лептоны) и частицами с целым спином (бозоны – фотон, глюоны,
W, Z…). Каждой известной частице должен соответствовать суперсимметричный
партнер, спин которого отличается на 1/2. Массы суперпартнеров должны быть
гораздо больше, чем у наблюдаемых сейчас