Иначе говоря, если xn
1) для всех n
2) для любого
Аналогично, если
1) для всех n
2) для любого
Определение 8. Верхняя
(нижняя) грань множества значений числовой
последовательности {xn} называется верхней
(нижней) гранью этой последовательности и
обозначается sup {xn} (
соответственно inf {xn}).
Иначе говоря, если xn ![]() R,
n = 1, 2, ..., и если
R,
n = 1, 2, ..., и если ![]() = sup {xn}, то:
= sup {xn}, то:
1) для всех n ![]() N
имеет место неравенство xn <
N
имеет место неравенство xn < ![]() ;
;
2) для любого ![]() ' <
' < ![]() существует такое n0
существует такое n0 ![]() N,
что
N,
что ![]() <
< ![]() '.
'.
Аналогично, если ![]() = inf {xn}, то:
= inf {xn}, то:
1) для всех n ![]() N
имеет место неравенство xn >
N
имеет место неравенство xn > ![]() ;
;
2) для любого ![]() '
>
'
> ![]() существует такое n0
существует такое n0
![]() N,
что
N,
что ![]() <
< ![]() '.
'.
Примеры.
1. sup {1/n} = 1, inf {1/n} =
0.
2. sup {n} = +![]() , inf {n} = 1.
, inf {n} = 1.
Определение 9. Числовая
последовательность {xn} называется возрастающей
(убывающей), если для всех n ![]() N
выполняется неравенство xn < xn+1
( соответственно неравенство xn > xn+1).
N
выполняется неравенство xn < xn+1
( соответственно неравенство xn > xn+1).
Возрастающая (убывающая)
последовательность обозначается xn![]() (соответственно xn
(соответственно xn![]() ). Если возрастающая (убывающая)
последовательность имеет предел, равный a,
то пишут xn
). Если возрастающая (убывающая)
последовательность имеет предел, равный a,
то пишут xn![]() a
a
(соответственно xn![]() a).
a).
Последовательность {xn}
называется строго возрастающей (строго
убывающей), если для всех n ![]() N
выполняется неравенство xn < xn+1
(соответственно неравенство xn > xn+1).
Строго возрастающая (строго убывающая)
последовательность обозначается xn
N
выполняется неравенство xn < xn+1
(соответственно неравенство xn > xn+1).
Строго возрастающая (строго убывающая)
последовательность обозначается xn![]()
![]() (соответственно xn
(соответственно xn![]()
![]() ).
).
Убывающие и возрастающие
последовательности называются монотонными,
а строго убывающие и строго возрастающие - строго
монотонными.
Примеры.
3. Последовательность {1/n} строго
убывает.
4. Последовательность {n} строго
возрастает.
5. Последовательность {(-1)n}
немонотонная.
Теорема 3 (Beйepштpacc). Всякая возрастающая числовая последовательность {xn} имеет предел: конечный, если она ограничена сверху, и бесконечный, если она неограничена сверху, причем
|
(5.49) |
Аналогично, если {xn} - убывающая последовательность, то существует (конечный или бесконечный) предел
|
(5.50) |
и, следовательно, этот предел конечен, если последовательность {xn} ограничена снизу, и бесконечен, если она неограничена снизу.
|
![]() Пусть последовательность {xn}
возрастает. Докажем равенство (5.49). Остальные
утверждения теоремы для возрастающих
послеовательностей следуют из него очевидным
образом.
Пусть последовательность {xn}
возрастает. Докажем равенство (5.49). Остальные
утверждения теоремы для возрастающих
послеовательностей следуют из него очевидным
образом.
Пусть ![]() = sup
{xn}, значение
= sup
{xn}, значение ![]() может быть как конечным, так и бесконечным.
Возьмем произвольную окресность U(
может быть как конечным, так и бесконечным.
Возьмем произвольную окресность U(![]() ) точки
) точки ![]() и обозначим через
и обозначим через ![]() ' ее левый конец (рис. 52).
Очевидно,
' ее левый конец (рис. 52).
Очевидно, ![]() ' <
' < ![]() . Согласно
определению верхней грани:
. Согласно
определению верхней грани:
1) для любого номера n ![]() N
имеет место неравенство
N
имеет место неравенство
xn < |
(5.51) |
2) существует такой номер n0, что
|
(5.52) |
В силу возрастания последовательности {xn} из (5.51) и (5.52) следует, что для всех номеров n > n0 выполняется неравенство
|
(5.53) |
и поскольку (![]() ',
',![]() ]
] ![]() U(
U(![]() )
, то при n > n0 имеет место
включение
)
, то при n > n0 имеет место
включение
xn |
(5.54) |
а это и означает, что ![]() является пределом последовательности {xn}.
является пределом последовательности {xn}.
Аналогично рассматривается случай xn![]() .
. ![]()
Замечание. Если [an,bn],
n = 1, 2, ..., - система вложенных
отрезков, длины которых стремятся к нулю, а ![]() - точка, принадлежащая всем
отрезкам этой системы, то
- точка, принадлежащая всем
отрезкам этой системы, то
|
(5.55) |
В самом деле, последовательность {an}
возрастает, а {bn} убывает, кроме
того (см. (4.25) в п. 4.5),
было показано, что ![]() =
sup {an} = inf {bn}.
Поэтому равенство (5.55) сразу следует из
теоремы 3.
=
sup {an} = inf {bn}.
Поэтому равенство (5.55) сразу следует из
теоремы 3.
Пример 6 (число e). Рассмотрим
последовательность
an = (1 + 1/n)n, n = 1, 2, ..., |
(5.56) |
и покажем, что она строго возрастает и ограничена сверху, а следовательно, согласно теореме 3 имеет конечный предел. Применив формулу бинома Ньютона, получим
|
(5.57) |
Из выражения, стоящего в правой части равенства, видно, что при переходе от n к n + 1 число слагаемых (которые все положительны) в написанной сумме возрастает на единицу и каждое слагаемое, начиная с третьего, увеличивается, так как становится больше выражение, стоящее в каждых круглых скобках, ибо
1 - s/n < 1 - s/(n + 1), s = 1, 2, ..., n-1, n = 2, 3, ...
Это означает строгое возрастание последовательности (5.56):
xn < xn+1, n = 1, 2, ... |
(5.58) |
Далее, поскольку
1 - s/n < 1, s = 1, 2, ..., n-1, n = 2, 3, ... |
(5.59) |
![]()
и поэтому
1/n! < 1/2n-1, n = 1, 2, ..., |
(5.60) |
то при n > 1 из равенства (5.57) получим
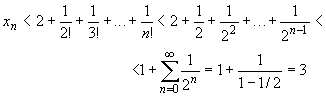
(мы заменили сумму конечной геометрической прогрессии суммой бесконечной геометрической прогрессии, так как у последней проще формула). Итак,
xn < 3, |
(5.61) |
т. е. последовательность (5.56) ограничена сверху. Из (5.58) и (5.61) следует, что она имеет конечный предел. Он обозначается через e
e |
(5.62) |
Поскольку 2 < xn < 3 и xn![]() , то 2 < e < 3. Можно
показать, что e - иррациональное число и
что с точностью до 10-15
, то 2 < e < 3. Можно
показать, что e - иррациональное число и
что с точностью до 10-15
e ![]() 2,718281828459045.
2,718281828459045.
Свойства пределов, связанные с арифметическими действиями над числовыми последовательностями Оглавление Принцип компактности