5.8. Принцип компактности
Если дана
последовательность {xn} и из некоторых
ее членов xnk, взятых в порядке
возрастания номеров nk (k > k'
равносильно nk > nk'),
составлена новая последовательность {xnk},
то она называется подпоследовательностью
последовательности {xn}.
В подпоследовательности {xnk}
k является номером члена этой
последовательности, а nk - его
номером в исходной последовательности. Ясно, что
для всех k = 1, 2, ... имеет место
неравенство nk > k, и
поэтому
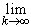 nk = +
nk = +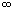 .
.
Подпоследовательности {xnk}
последовательности {xn} считаются
различными, если они соответствуют различным
наборам номеров {nk}. Различные
подпоследовательности одной и той же
последовательности, рассматриваемые как
последовательности, могут оказаться
одинаковыми. Так, последовательность xn = 0,
n = 1, 2, ..., как и любая
последовательность, имеет бесконечно много
различных подпоследовательностей (можно,
например, выбрать четные номера, нечетные,
кратные трем, четырем и т. д.), но все эти
подпоследовательности как последовательности
совпадают, очевидно, с данной
последовательностью xn = 0, n = 1, 2, ...
Выше было показано (см. п. 5.4), что если числовая
последовательность имеет конечный предел, то она
ограничена. Обратное, конечно, неверно. Например,
последовательность xn = (-1)n,
n = 1, 2, ..., ограничена, но не имеет
предела. Вместе с тем, если вся ограниченная
последовательность не имеет предела, то у нее
всегда существует подпоследовательность,
которая имеет предел. Точнее, имеет место
следующий факт.
Теорема 4. Из любой
ограниченной числовой последовательности можно
выделить сходящуюся подпоследовательность, а
из любой неограниченной сверху (неограниченной
снизу) числовой последовательности - последовательность,
имеющую своим пределом +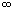 ( соответственно -
( соответственно -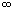 ).
).
 Рассмотрим сначала случай,
когда последовательность {xn}
ограничена, т. е. существуют такие a
Рассмотрим сначала случай,
когда последовательность {xn}
ограничена, т. е. существуют такие a  R
и
R
и
b  R, что для всех номеров n
выполняется неравенство a < xn < b.
Разделим отрезок [a,b] на два равных
отрезка точкой (a + b)/2. Тогда по
крайней мере на одном из них - обозначим его [a1,b1] -
окажется бесконечно много членов
последовательности {xn}. Выберем
произвольно какой-либо член этой
последовательности, содержащийся в отрезке [a1,b1].
Пусть его номер равен n1:
R, что для всех номеров n
выполняется неравенство a < xn < b.
Разделим отрезок [a,b] на два равных
отрезка точкой (a + b)/2. Тогда по
крайней мере на одном из них - обозначим его [a1,b1] -
окажется бесконечно много членов
последовательности {xn}. Выберем
произвольно какой-либо член этой
последовательности, содержащийся в отрезке [a1,b1].
Пусть его номер равен n1:
xn1 [a1,b1],
b1 - a1 = (b - a)/2. [a1,b1],
b1 - a1 = (b - a)/2. |
(5.63) |
Снова разделим отрезок [a1,b1]
на два равных отрезка и тот из них, на котором
лежит бесконечно много членов
последовательности (по крайней мере для одного
из них это условие выполняется), обозначим [a2,b2].
Поскольку на отрезке [a2,b2]
лежит бесконечно много членов
последовательности {xn}, то среди них
заведомо есть члены с номерами, большими чем n1.
Выберем один из таких членов. Если его номер n2,
то
xn2 [a2,b2] [a2,b2]
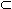 [a1,b1],
n2 > n1, [a1,b1],
n2 > n1, |
(5.64) |
b2 - a2 = (b1
- a1)/2 = (b - a)/22. |
(5.65) |
Продолжая этот процесс, получим такую
подпоследовательность {xnk}
(т. е. n1 < n2 ... < nk < ...)
последовательности {xn}, что
ak < xnk
< bk, |
(5.66) |
[ak,bk] 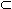 [ak-1,bk-1], [ak-1,bk-1], |
(5.67) |
bk - ak = (b
- a)/2k, k = 1, 2, ..., |
(5.68) |
и, следовательно, 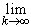 (bk
- ak) =
(bk
- ak) = 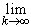 [(b - ak)2k]
= 0.
[(b - ak)2k]
= 0.
В результате получилась система
вложенных отрезков [ak,bk],
k = 1, 2, ..., длины которых стремятся к нулю.
Поэтому (см. п. 4.5)
существует единственная точка 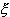 , принадлежащая всем этим отрезкам, причем (см. (5.55))
, принадлежащая всем этим отрезкам, причем (см. (5.55)) 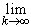 ak=
ak=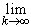 bk=
bk=
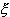 , а тогда в силу свойства 2o
пределов (см. п. 5.3) из неравенства (5.66)
следует, что
, а тогда в силу свойства 2o
пределов (см. п. 5.3) из неравенства (5.66)
следует, что
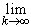 xnk=
xnk=
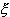 .
.
Это означает, что подпоследовательность {xn},
имеет конечный предел, т. е. сходится.
Пусть теперь последовательность {xn},
n = 1, 2, ..., не ограничена сверху. Тогда
существует такой номер n1, что xn1 > 1.
Поскольку последовательность xn1+1,
xn1+2, ..., получающаяся из данной
последовательности {xn} отбрасыванием
конечного числа ее членов x1, x2,
...xn1, также не ограничена
сверху, то найдется такой номер n2 > n1,
что xn2> 2. Продолжая этот
процесс, получим такие члены xnk
последовательности {xn}, что
| n1 < n2 <
... <nk < ..., |
(5.69) |
| xnk > k,
k = 1, 2, ... |
(5.70) |
Условие (5.69) означает, что последовательность {xnk}
является подпоследовательностью
последовательности {xn}, а из
условия (5.70) в силу следствия свойства 2o пределов (п. 5.3)
вытекает, что
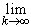 xnk
= + xnk
= +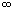 . . |
(5.71) |
Аналогично рассматривается случай
последовательности, не ограниченной снизу. 
Замечание 1. Первое
утверждение теоремы 4, т. е. то, что из
всякой ограниченной числовой
последовательности можно выделить сходящуюся,
называется теоремой Больцано-Вейерштрасса или принципом
компактности отрезка.
Замечание 2. Поскольку всякая
неограниченная последовательность не
ограничена по крайней мере либо сверху, либо
снизу, то из второго утверждения теоремы 4
следует, что всякая неограниченная
последовательность содержит бесконечно большую
подпоследовательность, причем ее всегда можно
выбрать таким образом, что ее пределом будет
являться бесконечность со знаком.
Определение 10. Предел,
конечный или определенного знака бесконечный,
подпоследовательности числовой
последовательности называется частичным
пределом этой последовательности.
Из теоремы 4 следует, что у любой
числовой последовательности всегда существует
по крайней мере один частичный предел (заведомо
конечный, если последовательность ограничена, и
бесконечный, если она не ограничена).
Монотонные
последовательности Оглавление
Критерий Коши