12.2. Теоремы Ролля, Лагранжа и Коши о средних значениях

    Теорема 2 (Ролль). Если функция f:
    1) непрерывна на отрезке [a,b];
    2) имеет в каждой точке интервала (a,b) конечную или определенного знака бесконечную производную;
    3) принимает равные значения на концах отрезка [a,b] , т. е.

то существует по крайней мере одна такая точка  (a,b) , что

   Геометрический смысл теремы Ролля состоит в том, что на графике функции, удовлетворяющей условиям теоремы Ролля, имеется по крайней мере одна точка, в которой касательная горизонтальна (рис. 78).
Если для любой точки x интервала (a,b) выполняется равенство f(x) = f(a) = f(b), то функция f является постоянной на этом интервале, и потому для любой точки  (a,b) выполняется условие (12.4).
    Пусть существует точка x₀  (a,b), для которой f(x₀)f(a), например f(x₀) > f(a). Согласно теореме Вейерштрасса о достижимости непрерывной на отрезке функцией своих наибольшего и наименьшего значений (см. теорему 1 в п. 7.1), существует такая точка [a,b], в которой функция f принимает наибольшее значение. Тогда

f() > f(x₀) > f(a) = f(b),

Поэтому a и b, т. е. точка принадлежит интервалу (a,b) и функция f принимает в ней наибольшее значение. Следовательно, согласно теореме Ферма (см. теорему 1 в п. 12.1), выполняется равенство f'() = 0. 
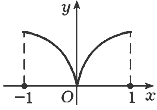
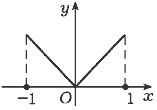
    Замечание 3. Все условия теоремы Ролля существенны. На рис. 79 изображены графики четырех функций, определенных на отрезке [-1,1]; у каждой из ниeх не выполняется лишь одно из трех условий теоремы Ролля и не существует такой точки , что f'() = 0. Пример функции  (см. рис. 79, б) показывает также, что условие существования определенного знака бесконечной производной нельзя заменить условием существования просто бесконечной производной. У функции в точке x = 0 производная равна бесконечности, но без определенного знака, т. е. f'(0) = , и не существует такой точки , что f'() = 0.

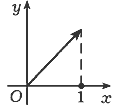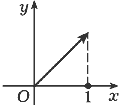= 1 - точка разрыва а	f'(0) = б	f'(0) не существует в	f(0) = f(1) г
Рис. 79

     Примером функции, удовлетворяющей условиям теоремы Ролля и имеющей в некоторой точке определенного знака бесконечную производную, является функция

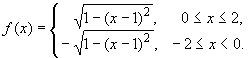
Эта функция непрерывна на отрезке [-2,2], дифференцируема во всех точках интервала (-2,2), кроме точки x = 0, в которой f'(0) = +,
и f(-2) = f(-2) (см. рис. 78). В согласии с теоремой Ролля у нее имеются точки, в которых производная равна нулю: ими являются точки x = +1. Графиком этой функции являются две полуокружности радиуса единица, сопряженные в точке (0).

    Замечание 4. В дальнейшем нам понадобится следующее свойство бесконечных производных. Если функции y₁ = f₁(x) и y₂ = f₂(x) определены в окрестности точки x₀, функция f₁ имеет в точке x₀ бесконечную производную (определенного знака или нет), а функция f₂ имеет в точке x₀ конечную производную, то функция y = f₁(x) + f₂(x)   имеет в точке x₀ такую же бесконечную производную, как и функция f₁. Для того чтобы в этом убедиться, надо перейти к пределу при x0 в равенстве

y/x = y₁/x + y₂/x.

    Теорема 3 (Лагранж). Если функция f непрерывна на отрезке [a,b] и в каждой точке интервала (a,b) имеет конечную или определенного знака бесконечную производную, то существует такая точка  (a,b), что

Это равенство называется формулой конечных приращений Лагранжа.
    Рассмотрим вспомогательную функцию

где  - некоторое число. Эта функция непрерывна на отрезке [a,b] и в каждой точке интервала (a,b) имеет конечную или определенного знака бесконечную производную (см. замечание 4). Подберем число  так, чтобы выполнялось соотношение

тогда функция F будет удовлетворять всем условиям теоремы Ролля. Из условий (12.6) и (12.7) имеем равенство f(a) - a = f(b) - b, откуда

При этом , согласно теореме Ролля, существует такая точка  (a,b), что

и так как из (12.6) следует, что F'(x) = f'(x) - , то из (12.8) и (12.9) получаем

что равносильно равенству (12.5). 

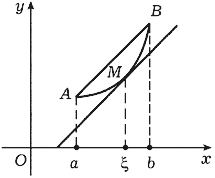    Геометрический смысл теоремы Лагранжа состоит в том, что на дуге (рис. 80) графика функции f с концами в точках A = (a, f(a)) и B = (b, f(b)) найдется точка M = (, f()), касательная в которой параллельна хорде AB. Действительно, согласно теореме Лагранжа

где [f(b) - f(a)]/(b - a) - тангенс угла наклона хорды AB, а  f'()- тангенс угла наклона касательной к дуге в точке M = (, f()), (a,b).
    Если положить ( - a)/(b - a), a < < b, то, очевидно, 0 <  < 1 и = a + (b - a). Поэтому формулу Лагранжа можно также записать в виде

f(b) - f(a) = f'(a + (b - a))(b - a),   0 <  < 1

или, полагая b - a = x, a = x и, следовательно, b = x + x, в виде

    Заметим, что равенство (12.10) остается верным и при b < a (а поэтому и равенство (12.11) при x < 0), так как при перемене местами a и b его левая часть не меняет знака, причем в этом случае также
= a + (b - a), 0 <  < 1 (здесь b - a < 0,  - a < 0).

    Следствие 1. Если фукция непрерывна и имеет производную, равную нулю, во всех точках некоторого промежутка (конечного или бесконечного), то она на нем постоянна.
Действительно, пусть функция f удовлетворяет сформулированным условиям на некотором промежутке и x₁, x₂ - две произвольные его точки, x₁ < x₂. Тогда функция f непрерывна и дифференцируема на отрезке [x₁,x₂] (на концах этого отрезка в смысле соответственно односторонней непрерывности и односторонних производных). По теореме Лагранжа

Во всех точках промежутка, на котором рассматривается функция f, по условию f'(x) = 0, в частности f'() = 0. Поэтому из равенства (12.12) следует, что f(x₂) = f(x₁).
    Поскольку x₁ и x₂ - произвольные точки указанного промежутка, то это и означает, что функция f на нем постоянна. 

    Следствие 2. Если функция f непрерывна в окрестности U(x₀) точки x₀, дифференцируема в проколотой окрестности (x₀) и существует конечный или бесконечный предел

f'(x),

то существует конечная или бесконечная производная f'(x₀) и

f'(x₀) =f'(x),

    В частности, производная не может иметь устранимую точку разрыва.
В самом деле, согласно теореме Лагранжа для любой точки x (x₀) справедливо равенство

где = (x) лежит между точками x₀ и x, и, следовательно, (x) = x₀, а потому

    Из этого равенства следует, что левая часть равенства (12.13) имеет конечный или бесконечный предел, т. е. существует конечная или бесконечная производная f'(x₀), причем

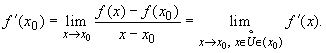
    Утверждение, аналогичное следствию 2, имеет место и для односторонних производных.

    Замечание 5. Из следствия 2 вытекает, что если функция f непрерывна на некотором промежутке (конечном или бесконечном) и имеет производную, равную нулю во всех точках этого промежутка, кроме, быть может, конечного множества его точек, то функция f постоянна на указанном промежутке. Действительно, в этом случае в достаточно малых проколотых окрестностях точек рассматриваемого конечного множества производная функции равна нулю и, следовательно, имеет в этих точках предел, равный нулю по проколотым окрестностям. Согласно следствию 2 в указанных точках также существует производная и она равна нулю. Поэтому в силу следствия 1 функция является постоянной.

    Теорема 4 (Коши). Если функции f и g:
    1) непрерывны на отрезке [a,b];
    2) дифференцируемы в каждой точке интервала (a,b);
    3) g'(x)0 во всех точках x (a,b);
то существует такая точка  (a,b), что

Прежде всего заметим, что для функции g справедливо неравенство

так как если бы имело место равенство g(a) = g(b), то в силу теоремы Ролля нашлась бы такая точка
x₀  (a,b), что g'(x₀) = 0, а это противоречило бы условиям теоремы. В силу неравенства (12.16) левая часть формулы (12.15) имеет смысл. Рассмотрим теперь функцию

где число подберем таким образом, чтобы имело место равенство

Тогда функция F будет удовлетворять на отрезке [a,b] условиям теоремы Ролля. Из соотношений (12.17) и (12.18) имеем

f(a) - g(a) = f(b) - g(b),

откуда

     При таком выборе числа существует  (a,b), для которого F'() = 0, то F'() = f'(x) - g'(x), следовательно,

f'(x) - g'(x) = 0,

и поэтому

Из (12.19) и (12.20) следует (12.15).

Теорема Ферма  Оглавление  Раскрытие неопределенностей вида 0/0