7.1. Ограниченность непрерывных функций.
Достижимость экстремальных значений
Определение 1. Функция
называется непрерывной на множестве, если
она непрерывна в каждой его точке.
Теорема 1 (Вейерштрасс). Всякая
непрерывная на отрезке функция ограничена и
достигает на нем своей верхней и своей нижней
граней. Иначе говоря, непрерывная на отрезке
функция принимает как свое наибольшее, так и свое
наименьшее значение (см. п. 3.1).
 Пусть функция f
непрерывна на отрезке [a,b] и
Пусть функция f
непрерывна на отрезке [a,b] и 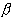 =
= 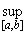 f(x). Покажем, что
f(x). Покажем, что 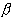 < +
< +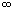 и что существует такое x0
и что существует такое x0  [a,b], что f(x0)
=
[a,b], что f(x0)
= 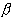 .
.
Пусть {yn} - такая
последовательность, что
yn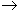 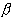 , n = 1,
2, ... , n = 1,
2, ... |
(7.1) |
Согласно определению верхней грани для каждого
n = 1, 2, ... найдется такое xn  [a,b], что
[a,b], что
f(xn)
> yn, n = 1, 2, ... |
(7.2) |
С другой стороны, поскольку 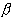 - верхняя грань функции f,
то для любого x
- верхняя грань функции f,
то для любого x  [a,b] выполняется
неравенство f(x) <
[a,b] выполняется
неравенство f(x) < 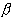 , в частности f(xn)
<
, в частности f(xn)
< 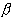 . Итак, yn
< f(xn) <
. Итак, yn
< f(xn) < 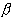 , n = 1, 2, ..., а поэтому
, n = 1, 2, ..., а поэтому
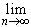 f(xn) f(xn)
|
= |
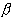 |
(7.3) |
|
(7.1) |
|
Последовательность {xn}
ограничена: a < xn < b, n = 1,
2, ... Следовательно, по теореме
Больцано-Вейерштрасса она содержит сходящуюся
подпоследовательность {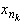 }. Обозначим ее предел через x0:
}. Обозначим ее предел через x0:
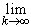 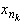 = x0. = x0.
|
(7.4) |
Поскольку a < 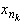 < b, то
< b, то
А так как {f(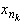 )}
является подпоследовательностью
последовательности {f(xn)}, то из (7.3)
имеем
)}
является подпоследовательностью
последовательности {f(xn)}, то из (7.3)
имеем
Но функция f непрерывна на отрезке [a,b],
в частности, в точке x0, поэтому из (7.4)
вытекает, что
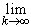 f( f(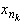 ) = f(x0). ) = f(x0).
|
(7.7) |
Следовательно,
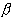
|
= |
f(x0) < +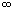 . . |
|
(7.6)
(7.7) |
|
Аналогично доказывается
ограниченность снизу функции f и
достижимость ее нижней грани. 
Предел и непрерывность
функций комплексного аргумента Оглавление Промежуточные
значения непрерывных функций