12.1. Теорема Ферма

    Пусть функция f задана на множестве  и x0 принадлежит X. Напомним, что если для всех точек x принадлежит X выполняется неравенство f(x) <  f(x0) (соответственно неравенство f(x) >  f(x0)), то говорят, что функция f принимает в точке x0 наибольшее (наименьшее) значение на множестве X (см. п. 3.1). Если в неравенстве f(x) <  f(x0) (соответственно в неравенстве f(x) >  f(x0)) заменить при xне равноx0 знак нестрогого неравенства на знак строгого неравенства, то получится определение точки x0, в которой функция f принимает строго наибольшее (строго наименьшее) значение на множестве X.

    Теорема 1 (Ферма). Если функция определена в некоторой окрестности точки, принимает в этой точке наибольшее (наименьшее) значение и имеет конечную или определенного знака бесконечную производную, то эта производная равна нулю.
Пусть функция f определена на окрестности U(x0) точки x0 и принимает в этой точке, например, наибольшее значение, т. е. для любой точки x принадлежит U(x0) выполняется неравенство f(x) <  f(x0). Тогда если x < x0, то

(12.1)

а если x > x0, то

(12.2)

    По условию теоремы существует конечный или определенного знака бесконечный предел

поэтому в неравенствах (12.1) и (12.2) можно перейти к пределу при xx0 (см. свойство 4o пределов функций в п. 6.7). В результате получим соответственно f'(x0) > 0 и f'(x0) < 0. Следовательно, f'(x0) = 0. конец
    Замечание 1. Формулировка теоремы Ферма на первый взгляд может показаться неестественной: в предположениях говорится о бесконечных производных, а в утверждении - о равенстве нулю производной. Однако на самом деле формулировка теоремы вполне корректна: a priori предполагается, что в точке существует производная (конечная или определенного знака бесконечная), и доказывается, что при выполнении дополнительного условия о достижении в рассматриваемой точке наибольшего или наименьшего значения указанная производная равна нулю. Иначе говоря, доказывается, что в точке, в которой принимается наибольшее в некоторой ее окрестности значение функции, не может существовать ни конечная, не равная нулю производная функции, ни определенного знака бесконечная производная. Поэтому в точке, в которой достигается наибольшее или наименьшее в ее окрестности значение функции, возможны следующие случаи: в этой точке существует конечная равная нулю производная; существует знаконеопределенная бесконечная производная; не существует никакой производной (ни конечной, ни бесконечной). 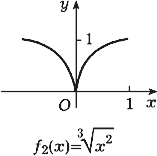Примером функции, для которой осуществляется первый случай, является функция f1(x) = x2; второй случай: ; третий: f3(x) = |x| (рис. 77).

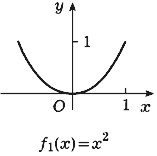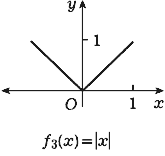Рис. 77a Рис. 77б Рис. 77в
Рис. 77

Все эти функции принимают при x = 0 наименьшее значение, f'1(x) = 0, f'2(x) = 0, производная (конечная или бесконечная) функции f3 в точке x = 0 не существует.
    Замечание 2. В теореме Ферма существенно, что точка, в которой достигается экстремальное значение, является внутренней для рассматриваемого промежутка. Так, например, функция f(x) = x, рассматриваемая только на отрезке [0,1], принимает наибольшее и наименьшее значения на его концах, а производная в них не обращается в нуль.

Дифференциалы высших порядков   Оглавление  Теоремы Ролля, Лагранжа и Коши о средних значениях