(x0)
= f(k)(x), k = 0,
1, ..., n,
(14.1)
Рассмотрим следующую задачу. Пусть функция y = f(x) имеет в точке x0 производные до порядка n включительно. Требуется найти такой многочлен Pn(x) степени не выше, чем n, что
|
(14.1) |
rn(x) |
(14.2) |
В случае n = 1 нам уже известно, что эта задача имеет решение и что ее решением является многочлен
P1(x) = f(x0) + f'(x0)(x - x0), |
(14.3) |
так как
P1(x) = f(x0),
P'1(x) = f'(x0),
r1(x) = f(x) - P1(x)
= f(x) - f(x0) - f'(x0)(x - x0)
=
= 
y - f'(x0)x = y - dy = o(x), x
0,
где, как обычно, x
= x - x0, y = f(x) - f(x0).
По аналогии с формулой (14.3) будем
искать многочлен Pn(x),
удовлетворяющий условиям (14.1) и (14.2), в виде
Pn(x) = a0 + a1(x - x0) + ...+ an(x - x0)n. |
(14.4) |
Положив x = x0, в силу условия (14.1) при k = 0 получим
a0 = f(x0). |
(14.5) |
Дифференцируя равенство (14.4), будем иметь
P'n(x) = a1 + 2a2(x - x0) + ...+ nan(x - x0)n-1.
Положив здесь x = x0, в силу условия (14.1) при k = 1 получим
a1 = f'(x0). |
(14.6) |
Вообще, продифференцировав равенство (14.4) k раз:
(x) = k!ak + (k +
1)...2ak+1(x - x0) + ...+
n(n - 1)...(n - k + 1)an(x - x0)n-k,
и положив x = x0, в силу условия (14.1) получим
ak = f(k)(x0)/k! k = 0, 1, ..., n, |
(14.7) |
Таким образом, если коэффициенты многочлена (14.4) выбраны согласно формулам (14.7), то этот многочлен удовлетворяет условию (14.1). Покажем, что он удовлетворяет и условию (14.2). Для этого прежде всего отметим, что в силу условий (14.1) для функции
rn(x) |
(14.8) |
имеет место
rn(x0) = r'n(x0)
= |
(14.9) |
Из того, что функция f(x) имеет в точке x0 производную порядка n, вытекает, что у нее в некоторой окрестности этой точки существуют производные до порядка n - 1 включительно и все производные функции f(x), а следовательно, в силу равенства (14.8) и производные функции rn(x), до порядка n - 1 включительно непрерывны в указанной точке x0 и
|
= | 0, k = 0, 1, ..., n - 1. |
| (14.9) |
Для вычисления предела 
[rn(x)/(x - x0)n]
применим сначала n - 1 раз правило
Лопиталя - теорему 2
из п. 13.1, а затем оттуда же теорему
1:
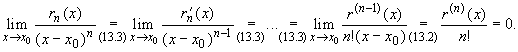
Это и означает выполнение условия (14.2). Итак,
доказана следующая
Теорема 1. Если функция f(x)
n раз дифференцируема в точке x0,
то в некоторой окрестности этой точки
|
(14.10) |
|
(14.11) |
называется многочленом Тейлора (порядка n), формула (14.10) - формулой Тейлора (порядка n) для функции f(x) в точке x = x0, а функция
rn(x) = f(x) - Pn(x) |
(14.12) |
- остаточным членом (порядка n) формулы Тейлора, а его представление в виде (14.2), т. е.
rn(x) = o((x - x0)n),
xx0,
- записью остаточного члена в виде Пеано.
Частный случай формулы Тейлора (14.10) при x0 = 0 называется формулой Маклорена
|
(14.13) |
где, согласно (14.2), остаточный член rn(x) можно записать в виде
rn(x) = o(x)n,
x |
(14.14) |
Из нижеследующей теоремы будет
следовать, что многочлен Тейлора единствен в
своем роде. Именно, никакой другой многочлен не
приближает функцию, заданную в окрестности точки
x0 с точностью до бесконечно малых того
же порядка относительно x - x0,
xx0, что и многочлен
Тейлора.
Предварительно отметим, что любой
многочлен 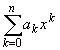Pn(x) = 
степени n для любого x0
может быть записан в виде Pn(x) =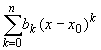 
. Действительно, положив
h = x - x0,
использовав формулу бинома Ньютона и собрав
члены с одинаковыми степенями h, получим
Pn(x) =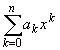 
,
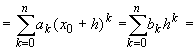
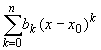где bk - некоторые постоянные.
Теорема 2. Если функция f(x) задана в окрестности точки x0 и имеет представление
f(x) = |
(14.15) |
то такое представление единственно.
Пусть наряду с
представлением (14.15) имеет место представление
f(x) = |
(14.16) |
Тогда, положив
ck = bk - ak, k = 0, 1, ..., n, |
(14.17) |
и вычтя из равенства (14.16) равенство (14.15), получим
|
(14.18) |
Перейдя в этом равенстве к пределу при xx0, получим c0 = 0.
Заметим, что o((x - x0)m)
= 
(x)(x - x0)m,
(x) = 0, и, следовательно, при x
x0, m = 1,
2, ...
o((x - x0)m)/
(x - x0) = (x)(x - x0)m-1
= o((x - x0)m-1), xx0.
Сократив на x - x0, xx0, левую часть
равенства (14.18) (в нем, как уже доказано, c0 = 0),
получим
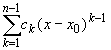+ o((x
- x0)n-1) = 0, xx0.
Перейдя в этом равенстве к пределу при xx0, xx0, получим c1 = 0.
Продолжая этот процесс после m-го шага, 0 < m < n,
получим
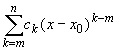+ o((x
- x0)n-m) = 0, xx0.
отсюда при xx0
следует, что cm = 0, m = 0, 1,
..., n.
Таким образом, в силу равенств (14.17)
ak = bk,
m = 0, 1, ..., n. 
Теорема 2 называется обычно теоремой единственности. Из нее следует, что если для n раз дифференцируемой в точке функции f получено представление ее в виде (14.15), то это представление является ее разложением по формуле Тейлора. В самом деле, при сделанных предположениях, согласно теореме 1, такое представление существует, а другого в силу теоремы 2 нет.
Неопределенности вида бесконечность/бесконечность Оглавление Примеры разложения по формуле Тейлора
f(x) - Pn(x)
= o((x - x0)n),
x
(x0) = 0.
(x) = r(k)(x0)
x
+ o((x - x0)n),
x
+ o((x
- x0)n) = 0, x