1. Напишем формулу Маклорена для функции f(x) = sin x.
Так как (sin x)(n) = sin (x + n
/2) (см. п. 11.1),
то Примеры.
1. Напишем формулу Маклорена для
функции f(x) = sin x.
Так как (sin x)(n) = sin (x + n/2) (см. п. 11.1),
то
f(n)(0) = |
k = 0, 1, 2,... |
Поэтому
sin x = x - |
(14.19) |
2. Для функции f(x) = cos x
имеем аналогично (cos x)(n) = cos (x + n/2),
f(n)(0) = |
k = 0, 1, 2,... |
поэтому
cos x = 1 - |
(14.20) |
3. Рассмотрим функцию f(x) = ex. Так как (ex)(n) = ex, то f(n)(0) = 1 и, следовательно,
ex = 1 + x + |
(14.21) |
Отсюда следует, что
e-x = 1 - x + |
(14.22) |
Складывая и вычитая соотношения (14.21) и (14.22), после умножения результата на 1/2 получим
ch x = (ex + e-x)/2
= 1 + |
(14.23) |
sh x = (ex - e-x)/2
= x + |
(14.24) |
В силу теоремы единственности (см. теорему 2 в п. 14.1)
полученные разложения являются разложениями
функций ch x и sh x по формуле
Тейлора.
4. Если f(x) = (1+ x)a,
a 
R, a 
N, то
f(n)(x) = a(a - 1)...(a - n + 1)(1+ x)a-n.
Поэтому
f(n)(0) = a(a - 1)...(a - n + 1)(1+ x)a-n, n = 1, 2,..., f(0) = 1;
отсюда
(1+ x)a = 1 + ax +
|
(14.25) |
Если a = m - натуральное число, то при n > m будем иметь (1+ x)m = Pm(x), где Pm(x) - многочлен степени m. Отсюда, согласно теореме единственности, следует, что Pm(x) является многочленом Тейлора, и, следовательно, в силу (14.25)
(1+ x)m = 1 + mx + 
+ ... + xm,
т. е. в этом случае формула (14.25) превращается в формулу бинома Ньютона.
5. Пусть f(x) = ln (1+ x); тогда
f'(x) = (1+ x)-1, f"(x) = (-1)(1+ x)-2,
вообще, f(n)(x) = (-1)n+1(n - 1)!(1+ x)-n, поэтому
f(n)(0) = (-1)n+1(n - 1)!, + O(x2n+3)
и так как f(0) = 0, то
ln (1+ x) = x - |
(14.26) |
Замечание. Отметим, что
axn + o(xn)
= O(xn), x |
(14.27) |
Действительно, o(xn) = 
(x)xn, где 
(x)
= 0. Поэтому существует такое 
> 0, что при |x| < имеем
|(x)| < 1 и,
следовательно,
|axn + o(xn)| = |axn
+ (xn)| <
(|a| + 1)|xn|.
Это и означает, что выполняется равенство (14.27).
Если в формуле Маклорена (14.13), (14.14)
заменить n на n + 1 (в предположении,
конечно, существовании производной порядка n + 1
при x = 0) и воспользоваться равенством
(14.27), то получим
f(x) =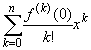 
+ O(xn+1), x
0.
Получившаяся оценка остатка rn(x) = O(xn+1) является, очевидно, более сильной, чем его оценка в формуле (14.13), где
rn(x) = o(xn),
x0.
Поэтому формула Тейлора для sin x,
cos x, ex, sh x, ch x, (1+ x)a
и ln (1+ x) можно при x0
записать в виде
sin x =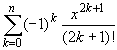 
+ O(x2n+3),
cos x =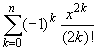 
+ O(x2n+2),
ex =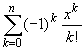 
+ O(xn+1),
sh x =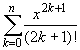 
+ O(x2n+3),
ch x =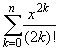 
+ O(x2n+2),
n = 0, 1,...,
(1+ x)a = 1 +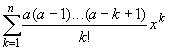 
+ O(xn+1),
ln (1+ x) =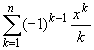 
+ O(xn+1),
n = 1, 2,...
+ o(x2n+2), x
+ o(x2n+1),
x
+ o(xn),
x
+ o(xn),
x
+ o(x2n+1),
x
+ o(x2n+2),
x
+ o(xn),
x
+ o(xn),
x