Пусть функция f представлена в окрестности точки x0 по формуле Тейлора в виде
f(x) = P(x) + o((x -
x0)), x![]() x0
x0
Многочлен Тейлора P(x) (если он не тождественный нуль) называют главной частью функции f в рассматриваемой окрестности. Ее выделение полезно применять для нахождения пределов функций. Покажем на примерах, как это делается.
Примеры.
1. Найти ![]() [(x - sin x)/x3].
Представим sin x, согласно формуле Тейлора,
в виде
[(x - sin x)/x3].
Представим sin x, согласно формуле Тейлора,
в виде
sin x = x - x3/6 + o(x4),
x![]() 0.
0.
В соответствии с теоремой 1 п. 9.3
x - sin x = x - (x - x3/6
+ o(x4)) = x3/6 + o(x4)
~ x3/6, x![]() 0.
0.
Поэтому, применив теорему 2 п. 9.3, получим
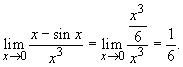
2. Найти ![]() .
.
Имеем
xcos x = x(1 + o(x)) = x +
o(x2),
(1 + 2x)1/2 = 1 + x - x2/2 +
o(x2),
ln (1 + x) = x - x2/2 + o(x2),
x![]() 0.
0.
Поэтому, согласно теоремам 1 и 2 из п. 9.3, с помощью этих соотношений будем иметь
![]()
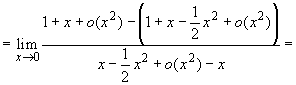
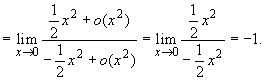
Мы воспользовались здесь тем, что
x2/2 + o(x2) ~ x2/2
и - x2/2 + o(x2) ~ -x2/2,
x![]() 0.
0.
3. Найти предел ![]()
![]() . Заметив, что
. Заметив, что ![]() =
= ![]() , найдем предел
натурального логарифма функции, стоящей под
знаком предела, т. е. предел
, найдем предел
натурального логарифма функции, стоящей под
знаком предела, т. е. предел
![]() (ctg2 x ln
cos x).
(ctg2 x ln
cos x).
Имеем
cos x = 1 - x2/2 + o(x2),
x![]() 0.
0.
Поэтому
ln cos x = ln (1 - x2/2 + o(x2))
= - x2/2 + o(x2),
x![]() 0.
0.
Далее,
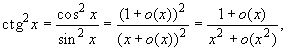 x
x![]() 0.
0.
Следовательно,
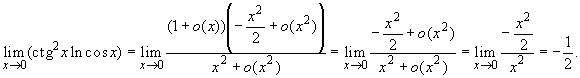
Тем самым найден и искомый предел:
![]()
Примеры разложения по формуле Тейлора Оглавление Признак монотонности функций