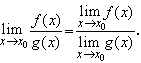6.7. Свойства пределов функций
В пп. 6.7-6.12 все рассматриваемые
функции определены на некотором фиксированном
множестве X 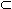 R и x0 - его точка
прикосновения, конечная или бесконечно
удаленная.
R и x0 - его точка
прикосновения, конечная или бесконечно
удаленная.
Функция называется ограниченной
(сверху или снизу), если множество ее значений
ограничено (соответственно сверху или снизу).
1o. Если функция f
имеет в точке x0 конечный предел, то
существует такая окрестность U(x0)
точки x0, что функция f
ограничена на пересечении X  U(x0).
U(x0).
 Если
Если  f(x) = a
f(x) = a  R,
то существует такая окрестность U(x0)
точки x0, что для всех x
R,
то существует такая окрестность U(x0)
точки x0, что для всех x  X
X  U(x0)
выполняется включение f(x)
U(x0)
выполняется включение f(x)  U(a,1) (здесь в
качестве окрестности U(a) в
определении 6 взята окрестность U(a,1)),
т. е. неравенство a - 1 < f(x) < a + 1.
U(a,1) (здесь в
качестве окрестности U(a) в
определении 6 взята окрестность U(a,1)),
т. е. неравенство a - 1 < f(x) < a + 1. 
Следствие. Если функция f
непрерывна в точке x0, то
существует такая окрестность U(x0)
точки x0, что функция f
ограничена на
X  U(x0).
U(x0).
Это следует из того, что если функция f
непрерывна в точке x0, то она имеет в
этой точке конечный предел.
2o. (лемма о сохранении
знака). Если функция f имеет в точке x0
не равный нулю конечный предел
 f(x)
= a
f(x)
= a 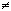 0, то существуют
такие окрестность U(x0) точки x0
и число c > 0, что для всех точек
0, то существуют
такие окрестность U(x0) точки x0
и число c > 0, что для всех точек
x  X
X  U(x0)
выполняются неравенства
U(x0)
выполняются неравенства
f(x) > c, если
a > 0;
f(x) > -c, если
a < 0.
 Поскольку a
Поскольку a 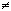 0, то |a|/2 > 0.
Возьмем в качестве окрестности U(a) в
определении 6 окрестность U(a, |a|/2)
. Тогда согласно этому определению существует
такая окрестность U(x0) точки x0,
что для всех точек
0, то |a|/2 > 0.
Возьмем в качестве окрестности U(a) в
определении 6 окрестность U(a, |a|/2)
. Тогда согласно этому определению существует
такая окрестность U(x0) точки x0,
что для всех точек
x  X
X  U(x0)
выполняется включение f(x)
U(x0)
выполняется включение f(x)  U(a, |a|/2),
т. е. справедливо неравенство
U(a, |a|/2),
т. е. справедливо неравенство
a - |a|/2 < f(x) < a + |a|/2.
Отсюда имеем при a > 0
f(x) > a - |a|/2 = a/2
> 0,
а при a < 0
f(x) < a + |a|/2 = -|a|
+ |a|/2 = -|a|/2 < 0,
Таким образом, неравенства (6.16)
выполняются при c = |a|/2. 
Следствие. Если функция f
непрерывна в точке x0 и f(x0)
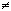 0,
0,
то существуют такие окрестность U(x0)
точки x0 и постоянная c > 0,
что для всех x  X
X  U(x0) выполняются
неравенства:
U(x0) выполняются
неравенства:
f(x) > c, если
f(x0) > 0;
f(x) > -c, если
f(x0) < 0.
Это сразу вытекает из свойства 2o,
поскольку непрерывность в точке x0
означает существование у функции f в точке x0
конечного предела, равного f(x0). В
качестве c можно взять | f(x0)|/2.
Замечание. Если у функции f в точке
x0 существует один из бесконечных
пределов 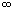 , +
, +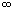 и -
и -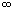 , то для любого числа c > 0
существует такая окрестность U(x0)
точки x0, что для любой точки x
, то для любого числа c > 0
существует такая окрестность U(x0)
точки x0, что для любой точки x  X
X  U(x0)
выполняются неравенства:
U(x0)
выполняются неравенства:
|f(x)| > c, если
 f(x) =
f(x) = 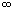 ;
;
f(x) > c, если  f(x) = +
f(x) = +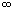 ;
;
f(x) > -c, если  f(x) = -
f(x) = -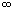 .
.
Это следует из определения
5 предела функции, в котором в качестве
окрестности U(a) бесконечно удаленной
точки в этом случае следует взять окрестность U(a,1/c).
3o. Если f(x) = c -
постоянная, x  X, то
X, то  f(x) = c.
Это означает, в частности, что постоянная функция
является непрерывной.
f(x) = c.
Это означает, в частности, что постоянная функция
является непрерывной.
4o. Если f(x) > a,
x  X и
существует конечный или определенного знака
бесконечный предел
X и
существует конечный или определенного знака
бесконечный предел  f(x), то
f(x), то  f(x)
> a.
f(x)
> a.
5o. Если 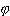 (x) < f(x)
<
(x) < f(x)
< 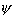 (x), x
(x), x  X и существуют
конечные или определенного знака бесконечные
пределы
X и существуют
конечные или определенного знака бесконечные
пределы 
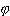 (x),
(x), 
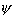 (x) и они равны между собой, то
существует
(x) и они равны между собой, то
существует  f(x) и
f(x) и
 f(x) =
f(x) = 
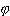 (x)
=
(x)
= 
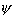 (x).
(x).
6o. Если существуют
конечные пределы  f(x) и
f(x) и  g(x), то
существуют и конечные пределы
g(x), то
существуют и конечные пределы
а если  g(x)
g(x)
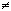 0, то и
0, то и
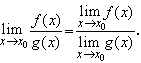 |
(6.19) |
В последнем случае функция 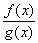 рассматривается только
для тех x, для которых g(x)
рассматривается только
для тех x, для которых g(x) 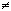 0 (см. свойство 2o).
0 (см. свойство 2o).
 Утверждения 3o-6o
следуют из соответствующих утверждений для
пределов последовательностей (см. пп. 5.3, 5.6)
Докажем, например, формулу (6.18). Пусть
Утверждения 3o-6o
следуют из соответствующих утверждений для
пределов последовательностей (см. пп. 5.3, 5.6)
Докажем, например, формулу (6.18). Пусть  f(x)
= a
f(x)
= a  R,
R,  g(x) = b
g(x) = b  R.
Возьмем какую-либо последовательность xn
R.
Возьмем какую-либо последовательность xn
 X, n = 1,
2, ..., имеющую своим пределом x0. Тогда
согласно определению 1
X, n = 1,
2, ..., имеющую своим пределом x0. Тогда
согласно определению 1 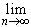 f(xn) = a,
f(xn) = a, 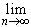 g(xn) = b, поэтому в силу
свойства пределов последовательностей (свойство 3o в
п. 5.6)
g(xn) = b, поэтому в силу
свойства пределов последовательностей (свойство 3o в
п. 5.6)
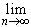 f(xn)g(xn)
=
f(xn)g(xn)
= 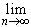 f(xn)
f(xn)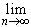 g(xn) = ab,
g(xn) = ab,
и поскольку последовательность {xn}
является произвольной последовательностью
такой, что xn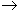 x0
и xn
x0
и xn  X,
n = 1, 2, ..., то согласно тому же
определению 1 предела функции получим
X,
n = 1, 2, ..., то согласно тому же
определению 1 предела функции получим
 f(x)g(x) = ab =
f(x)g(x) = ab =  f(x)
f(x) g(x).
g(x).
Следствие. Если функции f
и g непрерывны в точке x0  X,
X,
то функции  f(x)
+
f(x)
+ 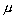 g(x),
g(x), 
 R,
R,
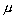
 R, f(x)g(x),
а если g(x0)
R, f(x)g(x),
а если g(x0)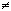 0, то и
0, то и 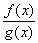 , непрерывны
в точке x0.
, непрерывны
в точке x0.
 Докажем,
например, непрерывность произведения f(x)g(x).
Если функции f и g непрерывны в точке x0,
то в этой точке они имеют конечные пределы f(x0)
и g(x0). Поэтому согласно формуле (6.18)
получим
Докажем,
например, непрерывность произведения f(x)g(x).
Если функции f и g непрерывны в точке x0,
то в этой точке они имеют конечные пределы f(x0)
и g(x0). Поэтому согласно формуле (6.18)
получим
 f(x)g(x) =
f(x)g(x) =  f(x)
f(x) g(x) = f(x0)g(x0)
g(x) = f(x0)g(x0)
Это и означает непрерывность произведения fg. 
Отметим, что проведенное
доказательство можно было бы и не проводить, так
как непрерывность функции в точке означает, что
(см. п. 6.2) эта точка
принадлежит множеству задания функции и что у
функции в этой точке существует предел по
указанному множеству. Поскольку функции f и g
заданы в точке x0, то, очевидно, и
функции  f(x) +
f(x) + 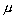 g(x), f(x)g(x), а при
g(x0)
g(x), f(x)g(x), а при
g(x0) 0 и
0 и 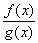 , заданы в этой точке. В
силу свойства 6o у перечисленных функций
существуют пределы в точке x0,
принадлежащей в данном случае их множеству
задания, что и означает их непрерывность в точке x0.
Иначе говоря, утверждение следствия является
просто частным случаем утверждения 6o,
когда точка, в которой рассматривается предел,
принадлежит области определения функций.
, заданы в этой точке. В
силу свойства 6o у перечисленных функций
существуют пределы в точке x0,
принадлежащей в данном случае их множеству
задания, что и означает их непрерывность в точке x0.
Иначе говоря, утверждение следствия является
просто частным случаем утверждения 6o,
когда точка, в которой рассматривается предел,
принадлежит области определения функций.
Односторонние пределы и
односторонняя непрерывность Оглавление
Бесконечно малые