19.1. Первообразная и неопределенный интеграл

    В этом параграфе рассматривается задача отыскания функции, для которой заданная функция является производной.
    Пусть  - конечный или бесконечный промежуток числовой оси, т. е. интервал, полуинтервал или отрезок (Если рассматриваемый промежуток является отрезком, то само собой разумеется, что он может быть только конечным.), и на заданы функции f и F.
    Определение 1. Функция F называется первообразной функцией (или, короче, первообразной) функции f на промежутке , если F дифференцируема на и в каждой точке этого промежутка производная функции F равна значению функции f:

    При этом если некоторый конец промежутка принадлежит этому промежутку, то под производной в этом конце, естественно, понимается соответствующая односторонняя производная. Поскольку функция, имеющая в данной точке производную, непрерывна в этой точке (односторонне непрерывна, если речь идет об односторонней производной), то первообразная F функции f непрерывна на промежутке .
    Пример. Функция F(x) = x³/3 является первообразной функции f(x) = x² на всей числовой оси.
    Иногда вместо слов "первообразная данной функции" говорят "первообразная для данной функции".
    Первообразная любой функции непрерывна, так как она имеет производную. Функция же, у которой существует первообразная, не обязательно непрерывна, например, у разрывной в нуле функции

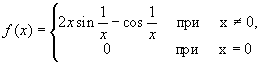
на всей числовой оси существует первообразная

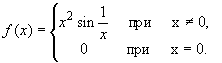
    Лемма 1. Для того чтобы две дифференцируемые на некотором промежутке функции были первообразными одной и той же функции, необходимо и достаточно, чтобы они на этом промежутке отличались на постоянную.
    Иначе говоря, функции F(x) и Ф(x) являются на промежутке первообразными одной и той же функции тогда и только тогда, когда

Если F - первообразная функции f, т. е. F' = f, то функция F + С является первообразной той же функции f, ибо (F + С)' = F' = f.
    Если F и Ф - первообразные для одной и той же функции f, т. е. F' = Ф' =  f, то (F - Ф)' = F' - Ф' = 0 и, следовательно, согласно следствию 1 теоремы Лагранжа (п. 12.2, теорема 3) разность F - Ф является постоянной на промежутке . 
    Определение 2. Пусть функция f задана на некотором промежутке . Совокупность всех ее первообразных на этом промежутке называется неопределенным интегралом от функции f и обозначается

    Если множество первообразных некоторой функции не пусто, то говорят, что у нее существует неопределенный интеграл. Таким образом, существование интеграла (на промежутке ) равносильно существованию у функции f первообразной на рассматриваемом промежутке. Если F - какая-либо первообразная функции f на рассматриваемом промежутке, то пишут

хотя правильнее было бы писать = {F(x) + С} (здесь и в дальнейшем С - произвольная постоянная).
    Иногда под понимается не совокупность всех первообразных функции f, а произвольный элемент этого множества, т. е. произвольная первообразная рассматриваемой функции. С разночтением одного и того же обозначения мы встречались и раньше, например, символом f(x) обозначается как сама функция, так и ее значение в точке x. Из контекста обычно всегда бывает ясно, в каком смысле в данном месте употреблено то или иное обозначение. Следует, однако, иметь в виду, что всякое равенство, в обеих частях которого стоят неопределенные интегралы, есть равенство между множествами.
    Под знаком интеграла пишут для удобства не саму функцию f, а ее произведение на дифференциал dx. Это делается, например, для того, чтобы указать, по какой переменной ищут первообразную:

Здесь в обоих случаях подынтегральная функция равна x²z, но ее неопределенные интегралы в первом и втором случаях различны, так как в первом случае она рассматривается как функция от переменной x, а во втором - как функция от z.
    Другие принципиально более важные удобства, вытекающие из использования записи , будут указаны в дальнейшем (см. замену переменной в интеграле в п. 19.4).
    Если F - какая-либо первообразная функции f на промежутке , то согласно формуле (19.4) под знаком интеграла стоит дифференциал функции F:

Будем считать по определению, что этот дифференциал под знаком интеграла можно записывать в любом из указанных видов, т. е. согласно этому соглашению

Кривизна и эволюта плоской кривой  Оглавление  Основные свойства интеграла