18.5. Кривизна и эволюта плоской кривой

    Пусть кривая Г = {r(t); a < t < b} лежит в некоторой плоскости; тогда и все производные векторной функции r(t), если их начало поместить на эту плоскость, будут также в ней лежать. В самом деле, приращение r = r(t₀ + t) - r(t₀) лежит в этой плоскости, поэтому лежит в ней и отношение r/t, а следовательно, и его предел (r/t) = r' . Применив те же рассуждения к r', получим, что и r" лежит в указанной плоскости и т. д. Отсюда следует, что если кривая лежит в некоторой плоскости, то касательная к кривой (а если ее кривизна k0, то и главная нормаль) лежит в той же плоскости. Поэтому эта плоскость является соприкасающейся плоскостью для рассматриваемой кривой.
    Запишем некоторые из формул, полученных в п. 18.4, более подробно для случая, когда кривая Г = {r(t); a < t < b} лежит в плоскости переменных x и y. В этом случае

r' = (x', y'),    r" = (x", y"),    |r'| = (x' ² +  y' ²)^1/2,
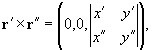     |r' x r'| = |x'y" - x"y'|.

Поэтому из формул (18.4) и (18.10) получаем следующую формулу для кривизны:

    Обозначим через (,) центр кривизны кривой Г. Из формул (18.27) и (18.28) следует, что

Аналогично,

    В случае когда кривая задается явно, т. е. функцией

(в этом случае x = t, x' = 1, x" = 0) s' = (1 + y' ²)^1/2, формулы (18.29), (18.30), (18.31) принимают вид

	(18.33)
	(18.34)

На примере кривой, имеющей явное задание, поясним, что кривизна кривой является угловой скоростью вращения касательной к этой кривой относительно длины ее дуги.
    Обозначим через угол, образованный касательной к кривой (18.7) с осью x (рис. 99), и будем его рассматривать как функцию длины дуги s этой кривой, а s в свою очередь, - как функцию переменной x.
Дифференцируя по x равенство y' = tg , получим

где (см. замечание 4 в п. 17.3) s' = (1 + y' ²)^1/2.
Поэтому y" = (1 + y' ²)^3/2d/ds, таким образом,

т. е. действительно кривизна кривой k равна абсолютной величине угловой скорости d/ds вращения касательной.
    Примеры.
    1. Найдем кривизну и эволюту параболы y² = 2px. Дважды дифференцируя это уравнение по x, получим yy' = p, y' ² + yy" = 0 и, следовательно,

y' = p/y,   y" = - y' ²/y = p²/y³,

Подставив эти выражения в формулу (18.33), найдем кривизну

и, подставив их в формулы (18.34), - уравнение эволюты

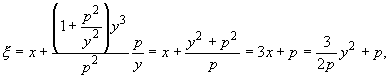	(18.38)
	(18.39)

    Таким образом, в получившемся уравнении эволюты параболы роль параметра играет переменная y; исключив ее из этих уравнений, получим

    Эта кривая, как мы знаем (п. 3.7), называется полукубической параболой (рис. 100).

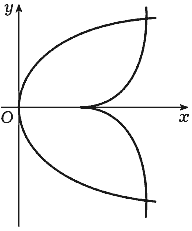Рис. 100

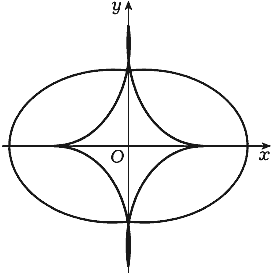Рис. 101

    2. Найдем радиус кривизны R и эволюту эллипса

x = acos t,    y = bsin t,     a > b > 0.

Заметив, что x' = -asin t, y' = bcos t, x" = -acos t, y" = -asin t, в силу формулы (18.29) получим

а из формул (18.30), (18.31) получим уравнение эволюты

Исключив из этих уравнений параметр t (для чего достаточно возвести их в степень 2/3 и сложить их), найдем уравнение эволюты в неявном виде

Полученная кривая называется астроидой (рис. 101).

Центр кривизны. Эволюта    Оглавление   Первообразная и неопределенный интеграл