25.1. Дифференцирование определенного интеграла по пределам интегрирования

    При изучении свойств интеграла была установлена (см. свойство 10^o в п. 24.1) его непрерывность по пределам интегрирования, т. е. непрерывность функций

F(x) = f(t)dt,     G(x) = f(t)dt,

на отрезке [a,b]. Оказывается, что с "улучшением" свойств подынтегральной функции f "улучшаются" и свойства функций F и G. Так, например, если функция f непрерывна на отрезке [a,b], то будет показано, что функции F и G являются уже дифференцируемыми.
    Докажем даже более точную теорему о дифференцируемости функции F в точке x₀.
    Теорема 1. Если функция f интегрируема на отрезке [a,b] и непрерывна в точке x₀ [a,b], то функция F(x) = f(t)dt дифференцируема в этой точке и

     Следствие. Всякая непрерывная на отрезке функция имеет на нем первообразную.
    Используя представление приращения F(x₀) в виде (см. (24.25))

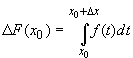, x₀ [a,b],   x₀ + x [a,b],

и тождество 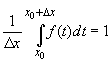, будем иметь

    Зададим произвольно > 0. В силу непрерывности функции f в точке x₀ существует такое > 0, что если |t - x₀| < и t [a,b], то

    Пусть x таково, что x < ; тогда для всех значений t, принадлежащих отрезку с концами x₀ и x₀ + x (по которому ведется интегрирование в неравенстве (25.2)), будем иметь |t - x₀| < |x|< и, следовательно,

Поэтому

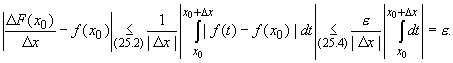
Это, согласно определению предела, и означает, что (F(x₀)/x) =  f(x₀), и, таким образом, формула (25.1) доказана. 
    Для доказательства следствия достаточно заметить, что равенство (25.1) в случае непрерывной на отрезке функции имеет место во всех точках этого отрезка.
    Замечание. Из доказанного следует, что в условиях теоремы 1 функция

G(x) = f(t)dt

также имеет производную в точке x₀ и

Это сразу следует из формулы (25.1), ибо (см. (24.26))

G(x) =  f(t)dt - F(x)

и  f(t)dt - постоянная величина.
    Если функция f непрерывна на отрезке [a,b], то для каждой его точки x справедливы формулы

Интегральная теорема о среднем  Оглавление Существование первообразной