25.2. Существование первообразной

    Теорема 2. Если функция f непрерывна во всех точках некоторого промежутка , то на этом промежутке у нее существует первообразная; при этом если x₀ - какая-либо точка рассматриваемого промежутка , то функция

является одной из первообразных функций f на промежутке .
    Достаточно проверить, что функция (25.7) действительно является первообразной функции f. Если x > x₀, x , то равенство F'(x) = f(x) сразу следует из теоремы 1. Если же x < x₀, x , то

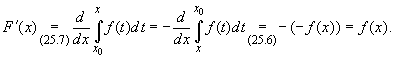
    Замечание1. Совокупность всех первообразных непрерывной на некотором промежутке функции f составляет неопределенный интеграл  f(x)dx, x , а определенный интеграл  f(t)dt , x₀ , x , является одной из первообразных функции f на . Поскольку две любые первообразные отличаются на постоянную, то

где C - произвольная постоянная. Так выглядит связь между неопределенным и определенным интегралами. Из теоремы 2 следует, что у всякой непрерывной на некотором промежутке функции существует на этом промежутке неопределенный интеграл.
    Теорема 3 (основная теорема интегрального исчисления). Если функция f непрерывна на отрезке [a,b], то, какова бы ни была на этом отрезке ее первообразная Ф, справедлива формула

называемая формулой Ньютона-Лейбница.
    По теореме 2 функция F(x) =  f(t)dt является первообразной функции f на отрезке [a,b]. Если Ф - какая-либо первообразная на [a,b] той же функции f, то они отличаются на постоянную, т. е. существует такая постоянная C, что для всех x [a,b] имеет место равенство

Положив здесь x = a и вспомнив, что  f(t)dt = 0, получим  C = - Ф(a). Подставив это значение в формулу (25.10), будем иметь

 f(t)dt = Ф(x) - Ф(a),   x [a,b].

    Формула (25.9) получается отсюда при x = a. 
    Отметим, что формула Ньютона-Лейбница (25.9) справедлива и для a > b. Действительно, если в ней поменять местами a и b, то обе части равенства (25.9) изменят знак на противоположный.
    Замечание 2. В формуле (25.9) Ф'(t) = f(t). Поэтому ее можно записать в виде

т. е. интеграл от непрерывной производной равен разности значений самой функции на концах отрезка, по которому производится интегрирование.
    Замечание 3. С помощью формулы (25.11) нетрудно показать, что формула Ньютона-Лейбница (25.9) остается верной и в случае, когда функция Ф непрерывна, а ее производная f кусочно непрерывна на отрезке [a,b] (см. замечание 3 в п. 24.1), а равенство выполняется во всех точках непрерывности функции f.
    Примером непрерывной первообразной кусочно непрерывной функции f является, например (см. теорему 1), функция

F(x) =  f(t)dt.

    Примеры.
    1. Вычислить значение интеграла x³dx. Поскольку x³dx = x⁴/4 + C, по по формуле Ньютона-Лейбница получим

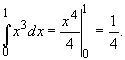
    2. Найдем значение интеграла cos x dx. Имеем

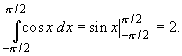
Дифференцирование определенного интеграла по пределам интегрирования  Оглавление   Формула замены переменной