![]() dx = b -
a.
dx = b -
a.
Перечислим свойства определенного интеграла, вытекающие непосредственно из того, что он является пределом интегральных сумм.
| 1o. |
|
![]() В данном случае
подынтегральная функция тождественно равна 1, и
потому при любом разбиении
В данном случае
подынтегральная функция тождественно равна 1, и
потому при любом разбиении ![]() все интегральные суммы Римана равны b - a:
все интегральные суммы Римана равны b - a:
|
(24.1) |
следовательно,
![]() dx =
dx = ![]()
![]() =
b - a.
=
b - a.
2o. Линейность
интеграла. Если функции f и g
интегрируемы на отрезке [a,b], то при
любых
![]()
![]() R
и
R
и ![]()
![]() R
функция
R
функция ![]() f +
f + ![]() g также интегрируема
на отрезке [a,b] и
g также интегрируема
на отрезке [a,b] и
|
(24.1) |
![]() Каковы бы ни
были разбиение
Каковы бы ни
были разбиение ![]() отрезка [a,b] и точки
отрезка [a,b] и точки ![]() k
k ![]() [xk-1,xk], k = 1,
2, ...,
[xk-1,xk], k = 1,
2, ..., ![]() , будем иметь
, будем иметь
|
(24.2) |
Поскольку при |![]() |
|![]() 0 предел правой части этого
равенства в силу интегрируемости функций f и
g существует, то существует при этом условии
и предел левой части
0 предел правой части этого
равенства в силу интегрируемости функций f и
g существует, то существует при этом условии
и предел левой части ![]()
![]() (
(![]() f
+
f
+ ![]() g) , что означает
интегрируемость функции
g) , что означает
интегрируемость функции ![]() f +
f + ![]() g.
Перейдя в равенстве (24.2) к пределу при |
g.
Перейдя в равенстве (24.2) к пределу при |![]() |
|![]() 0,
получим формулу (24.1).
0,
получим формулу (24.1). ![]()
3o. Если функция f
интегрируема на отрезке [a,b], то она
интегрируема и на любом отрезке
[a*,b*] ![]() [a,b].
[a,b].
![]() Из
интегрируемости функции f на отрезке [a,b]
следует ее ограниченность на нем, а
следовательно, и на отрезке [a*,b*]. Если
Из
интегрируемости функции f на отрезке [a,b]
следует ее ограниченность на нем, а
следовательно, и на отрезке [a*,b*]. Если ![]() - какое-либо разбиение
отрезка [a*,b*], то всегда, добавив к нему
соответствующее конечное множество точек,
лежащих на отрезках [a,b], но уже вне
отрезка [a*,b*], можно получить разбиение
- какое-либо разбиение
отрезка [a*,b*], то всегда, добавив к нему
соответствующее конечное множество точек,
лежащих на отрезках [a,b], но уже вне
отрезка [a*,b*], можно получить разбиение ![]() ,
, ![]() >
> ![]() ,
отрезка [a,b] той же мелкости
,
отрезка [a,b] той же мелкости
| |
(24.3) |
Обозначив посредством ![]() k(f)
и
k(f)
и ![]() колебания функции f
соответственно на отрезках [xk-1,xk]
и [
колебания функции f
соответственно на отрезках [xk-1,xk]
и [![]() ,
,![]() ] и заметив, что
] и заметив, что ![]()
![]() k( f )
k( f )![]() xk отличается
от
xk отличается
от 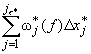 ,
, ![]() xk = xk - xk-1,
xk = xk - xk-1,
![]()
![]() =
= ![]() -
- ![]() , на неотрицательные
слагаемые вида
, на неотрицательные
слагаемые вида ![]() k(f)
k(f)![]() xk ,
соответствующие отрезкам [xk-1,xk]
разбиения
xk ,
соответствующие отрезкам [xk-1,xk]
разбиения ![]() , лежащим вне
отрезка [a*,b*], получим
, лежащим вне
отрезка [a*,b*], получим
0 < |
(24.4) |
Из интегрируемости функции f на отрезке [a,b],
согласно следствию 1
теоремы 2 из п. 23.5, вытекает, что
![]()
![]()
![]() k( f )
k( f )![]() xk = 0, поэтому в
силу (24.3) и (24.4)
xk = 0, поэтому в
силу (24.3) и (24.4) ![]()
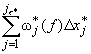 = 0 , а это, согласно тому
же следствию теоремы 2 п. 23.5, и означает
интегрируемость функции f на отрезке [a*,b*].
= 0 , а это, согласно тому
же следствию теоремы 2 п. 23.5, и означает
интегрируемость функции f на отрезке [a*,b*]. ![]()
4o. Аддитивность интеграла. Если функция f интегрируема на отрезке [a,b] и a < c < b, то
|
(24.5) |
![]() Если
Если ![]() и
и ![]() - разбиения соответственно отрезков [a,c]
и [c,b], то объединение этих разбиений
- разбиения соответственно отрезков [a,c]
и [c,b], то объединение этих разбиений
![]() =
= ![]()
![]()
![]() является разбиением отрезка [a,b],
причем
является разбиением отрезка [a,b],
причем
| |
(24.6) |
Пусть ![]() и
и ![]() - какие-либо
интегральные суммы Римана функции f,
соответствующие разбиениям
- какие-либо
интегральные суммы Римана функции f,
соответствующие разбиениям ![]() и
и ![]() ; тогда
; тогда
|
(24.7) |
- интегральная сумма Римана функции f на
отрезке [a,b].
Согласно свойству 2o из
интегрируемости функции f на отрезке [a,b]
следует ее интегрируемость на отрезках [a,c]
и [c,b]. Следовательно, интегральные
суммы ![]() ,
, ![]() и
и ![]() при условии, что мелкости разбиений
при условии, что мелкости разбиений ![]() , и стремятся к нулю, имеют
конечные пределы - интегралы от функции по
указанным отрезкам:
, и стремятся к нулю, имеют
конечные пределы - интегралы от функции по
указанным отрезкам:
![]() =
= ![]() f(x)dx,
f(x)dx,
![]() =
= ![]() f(x)dx,
f(x)dx, ![]() =
=![]() f(x)dx
f(x)dx
Поэтому, перейдя к пределу в равенстве (24.7) при
условии |![]() |
|![]() 0
(при этом в силу (24.6) |
0
(при этом в силу (24.6) |![]() |
|![]() 0 и |
0 и |![]() |
|![]() 0 ), получим формулу (24.5).
0 ), получим формулу (24.5). ![]()
Замечание 1. В силу
определения интеграла =![]() f(x)dx
при b < a (см. п. 23.1)
формула (24.5) остается в силе и при c > b,
если только функция f интегрируема на
отрезке [a,c].
f(x)dx
при b < a (см. п. 23.1)
формула (24.5) остается в силе и при c > b,
если только функция f интегрируема на
отрезке [a,c].
![]() В самом деле, если , то по
доказанному
В самом деле, если , то по
доказанному ![]() +
+ ![]() =
= ![]() и, следовательно,
и, следовательно, ![]() =
= ![]() -
-![]() =
= ![]() +
+ ![]() .
. ![]()
Замечание 2. Если функция f
интегрируема на отрезках и , то она интегрируема
и на отрезке [a,b], а следовательно, для
нее в силу свойства 3o имеет место
формула (24.5).
![]() Действительно, если функция f интегрируема
на отрезках [a,c] и [c,b], то она
ограничена на них, а поэтому ограничена и на
отрезке [a,b]. Далее, всякое разбиение
Действительно, если функция f интегрируема
на отрезках [a,c] и [c,b], то она
ограничена на них, а поэтому ограничена и на
отрезке [a,b]. Далее, всякое разбиение ![]() отрезка [a,b], не
содержащее точки x = c,
добавлением этой точки превращается в разбиение
отрезка [a,b], не
содержащее точки x = c,
добавлением этой точки превращается в разбиение ![]() ', которое является
объединением разбиений отрезков [a,c]
и [c,b]. Если точка x = c
входит в разбиение
', которое является
объединением разбиений отрезков [a,c]
и [c,b]. Если точка x = c
входит в разбиение ![]() , то
положим
, то
положим ![]() ' =
' = ![]() . Тогда |
. Тогда |![]() '| < |
'| < |![]() |. Рассмотрим такие интегральные
суммы
|. Рассмотрим такие интегральные
суммы ![]() и
и ![]() , что у них на отрезках
разбиений
, что у них на отрезках
разбиений ![]() и
и ![]() ', не содержащих точки x = c,
выбраны одинаковые точки, в которых берутся
значения функции f. Эти суммы отличаются
друг от друга не более чем на три слагаемых.
Поэтому, если | f(x)| < M, a < x < b,
то
', не содержащих точки x = c,
выбраны одинаковые точки, в которых берутся
значения функции f. Эти суммы отличаются
друг от друга не более чем на три слагаемых.
Поэтому, если | f(x)| < M, a < x < b,
то
|![]() -
- ![]() | < 3M|
| < 3M|![]() |
|![]() 0
при |
0
при |![]() |
|![]() 0
0
А так как существует предел
![]() =
= ![]() f(x)dx +
f(x)dx + ![]() f(x)dx,
f(x)dx,
то существует и равный ему предел
![]() ,
,
т. е. функция f интегрируема на отрезке [a,b]. ![]()
Замечание 3. Из
свойства аддитивности интеграла и из теоремы 4 п. 23.6
следует интегрируемость так называемых кусочно
непрерывных на отрезке функций.
Функция называется кусочно
непрерывной на отрезке, если она имеет на нем
только конечное множество точек разрыва, и
притом только первого рода. На концах отрезка
функция может быть не определена.
Таким образом, функция f кусочно
непрерывна на отрезке [a,b], если
найдется такое разбиение ![]() этого отрезка, что для всех k = 1,
2, ...,
этого отрезка, что для всех k = 1,
2, ..., ![]() существуют
конечные пределы f(xk-1 + 0) и f(xk - 0).
В точках xk, k = 1, 2, ...,
существуют
конечные пределы f(xk-1 + 0) и f(xk - 0).
В точках xk, k = 1, 2, ..., ![]() , функция f может
быть определена или не определена. Если положить
, функция f может
быть определена или не определена. Если положить
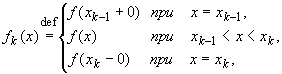
то функция fk будет непрерывна, а
поэтому, согласно теореме 4
п. 23.6, и интегрируема на отрезке [xk-1,xk],
k = 1, 2, ..., ![]() .
Отсюда следует интегрируемость функции f на
отрезке [a,b] (значения функции f в
тех точках xk, в которых она не
определена, можно задавать произвольно: это не
влияет ни на существование, ни на значение
интеграла) и справедливость формулы
.
Отсюда следует интегрируемость функции f на
отрезке [a,b] (значения функции f в
тех точках xk, в которых она не
определена, можно задавать произвольно: это не
влияет ни на существование, ни на значение
интеграла) и справедливость формулы
![]() f(x)dx
=
f(x)dx
=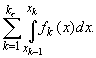
5o. Интегрируемость
произведения интегрируемых функций. Если
функции f и g интегрируемы на
некотором отрезке, то их произведение также
интегрируемо на этом отрезке.
![]() Если функции f
и g интегрируемы на отрезке [a,b], то
они на нем ограничены, т. е. существует такая
постоянная A > 0, что для всех x
Если функции f
и g интегрируемы на отрезке [a,b], то
они на нем ограничены, т. е. существует такая
постоянная A > 0, что для всех x ![]() [a,b]
выполняются неравенства
[a,b]
выполняются неравенства
| f(x)| < A, | g(x)| < A, |
(24.8) |
а следовательно, и | f(x)g(x)| < A2, т. е. произведение fg ограничено на отрезке [a,b]. Проверим для него выполнимость критерия (23.21) интегрируемости функций. Из тождества
f(x')g(x') - f(x)g(x)
= [ f(x') - f(x)]g(x')
+ [g(x') - g(x)] f(x),
x ![]() [a,b],
x'
[a,b],
x' ![]() [a,b]
[a,b]
имеем
| f(x')g(x') - f(x)g(x)| < | f(x') - f(x)||g(x')| + |g(x') - g(x)|| f(x)| < A| f(x') - f(x)| + |g(x') - g(x)|, |
(24.9) |
Если ![]() - разбиение
отрезка [a,b], то, выбирая точки x
и x' в одном и том же отрезке [xk-1,xk]
этого разбиения и переходя в неравенстве (24.9) к
верхним граням по всевозможным x
- разбиение
отрезка [a,b], то, выбирая точки x
и x' в одном и том же отрезке [xk-1,xk]
этого разбиения и переходя в неравенстве (24.9) к
верхним граням по всевозможным x ![]() [a,b]и x'
[a,b]и x' ![]() [a,b] ,
получим
[a,b] ,
получим
![]() k(fg) <
A[
k(fg) <
A[![]() k(f) +
k(f) + ![]() k(g)], k = 1, 2,
...,
k(g)], k = 1, 2,
..., ![]()
здесь ![]() k(
k(![]() )
, как обычно, - колебание соответствующей
функции на отрезке [xk-1,xk].
Отсюда
)
, как обычно, - колебание соответствующей
функции на отрезке [xk-1,xk].
Отсюда
|
(24.10) |
В силу интегрируемости функций f и g на отрезке [a,b] имеем (см. (23.21))
![]()
![]()
![]() k( f )
k( f )![]() xk =
xk = ![]()
![]()
![]() k(g)
k(g)![]() xk = 0.
xk = 0.
Поэтому из неравенства (24.10) следует, что ![]()
![]()
![]() k( fg)
k( fg)![]() xk = 0, откуда в силу того же
критерия (23.21) и вытекает интегрируемость
произведения fg.
xk = 0, откуда в силу того же
критерия (23.21) и вытекает интегрируемость
произведения fg. ![]()
6o. Интегрирование
частного интегрируемых функций. Если функции f
и g интегрируемы на некотором отрезке и
абсолютная величина функции g
ограничена на нем снизу положительной
постоянной, то частное f/g также
интегрируемо на этом отрезке.
![]() Покажем, что
при сделанных предположениях функция 1/g
интегрируема. Пусть функция g интегрируема
на отрезке [a,b] и существует такая
постоянная c > 0, что для всех точек x
Покажем, что
при сделанных предположениях функция 1/g
интегрируема. Пусть функция g интегрируема
на отрезке [a,b] и существует такая
постоянная c > 0, что для всех точек x
![]() [a,b]
выполняется неравенство g(x) > c.
Тогда для любых точек x,x'
[a,b]
выполняется неравенство g(x) > c.
Тогда для любых точек x,x' ![]() [a,b] имеем
[a,b] имеем
![]()
Если ![]() -
разбиение отрезка [a,b] и точки x,x'
содержатся в одном и том же отрезке [xk-1,xk],
k = 1, 2, ...,
-
разбиение отрезка [a,b] и точки x,x'
содержатся в одном и том же отрезке [xk-1,xk],
k = 1, 2, ..., ![]() ,
разбиения
,
разбиения ![]() , то переходя к
верхним граням в полученном неравенстве, будем
иметь
, то переходя к
верхним граням в полученном неравенстве, будем
иметь
![]()
Отсюда
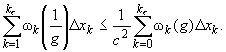
В силу интегрируемости функции g
правая часть неравенства стремится к нулю при |![]() |
|![]() 0.
Поэтому стремится к нулю и его левая часть. Это
означает интегрируемость функции 1/g на
отрезке [a,b].
0.
Поэтому стремится к нулю и его левая часть. Это
означает интегрируемость функции 1/g на
отрезке [a,b].
Если функция f также интегрируема
на этом отрезке, то частное f/g, будучи
произведением интегрируемых функций f и 1/g,
согласно свойству 5o также интегрируемо. ![]()
7o. Интегрирование неравенств. Если
функции f и g интегрируемы на
отрезке [a,b] и
f(x) > g(x),
x |
(24.11) |
то
|
(24.12) |
В частности, если f(x) > 0, x
![]() [a,b], то
[a,b], то
|
(24.13) |
![]() Из
неравенства (24.11) следует, что для любых
интегральных сумм
Из
неравенства (24.11) следует, что для любых
интегральных сумм ![]() (f) и
(f) и ![]() (g) соответственно функций f
и g выполняется неравенство
(g) соответственно функций f
и g выполняется неравенство
|
(24.14) |
ибо ![]() , k = 1, 2,
...,
, k = 1, 2,
..., ![]() . Переходя в
неравенстве (24.14) к пределу при |
. Переходя в
неравенстве (24.14) к пределу при |![]() |
|![]() 0, получим
неравенство (24.12).
0, получим
неравенство (24.12).
Неравенство (24.13) следует из
неравенства (24.12) при g(x) ![]() 0.
0. ![]() .
.
8o.Если функция f
интегрируема и неотрицательна на отрезке [a,b],
существует точка x0 ![]() [a,b], в которой функция
f непрерывна, и f(x0) > 0,
то
[a,b], в которой функция
f непрерывна, и f(x0) > 0,
то
![]() f(x)dx
> 0.
f(x)dx
> 0.
![]() Если функция
f непрерывна в точке x0
Если функция
f непрерывна в точке x0 ![]() [a,b] и f(x0) > 0,
то из очевидного неравенства f(x0) > f(x0)/2 > 0
согласно "лемме о сохранении знака" (см.
следствие из следствия 2o
в п. 6.7) следует, что существует такой отрезок [
[a,b] и f(x0) > 0,
то из очевидного неравенства f(x0) > f(x0)/2 > 0
согласно "лемме о сохранении знака" (см.
следствие из следствия 2o
в п. 6.7) следует, что существует такой отрезок [![]() ,
,![]() ],
что x0
],
что x0 ![]() [
[![]() ,
,![]() ]
]
![]() [a,b] ,
[a,b] ,![]() >
>![]() , и для всех точек x
, и для всех точек x ![]() [
[![]() ,
,![]() ] выполняется
неравенство
] выполняется
неравенство
f(x) > f(x0)/2 |
(24.15) |
а тогда
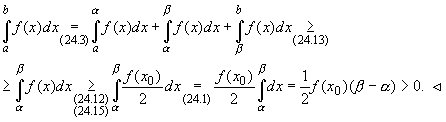
9o. Если функция f интегрируема на отрезке [a,b], то ее абсолютная величина| f| интегрируема на нем и
|
(24.16) |
![]() Прежде всего
из интегрируемости функции f следует ее
ограниченность, а следовательно, и
ограниченность функции | f |. Покажем,
что для функции | f | выполняется
критерий интегрируемости (23.21).
Прежде всего
из интегрируемости функции f следует ее
ограниченность, а следовательно, и
ограниченность функции | f |. Покажем,
что для функции | f | выполняется
критерий интегрируемости (23.21).
Заметив, что для любых двух точек x
![]() [a,b] и x'
[a,b] и x'
![]() [a,b]
справедливо неравенство
[a,b]
справедливо неравенство
|| f(x')| - | f(x)|| < | f(x') - f(x)|, |
(24.17) |
рассмотрим какое-либо разбиение ![]() отрезка [a,b].
Тогда, выбирая точки x и x' из одного и
того же отрезка [xk-1,xk] этого
разбиения, x
отрезка [a,b].
Тогда, выбирая точки x и x' из одного и
того же отрезка [xk-1,xk] этого
разбиения, x ![]() [xk-1,xk],
x'
[xk-1,xk],
x' ![]() [xk-1,xk],
и переходя в обеих частях неравенства (24.17) к
верхним граням, будем иметь
[xk-1,xk],
и переходя в обеих частях неравенства (24.17) к
верхним граням, будем иметь
![]() k(| f |)
=
k(| f |)
=![]() || f(x')| - | f(x)||
<
|| f(x')| - | f(x)||
< ![]() | f(x')
- f(x)| =
| f(x')
- f(x)| = ![]() k(f),
k(f),
где ![]() k(| f |) и
k(| f |) и ![]() k(f) - колебания
соответственно функций | f | и f на
отрезке [xk-1,xk], k = 1,
2, ...,
k(f) - колебания
соответственно функций | f | и f на
отрезке [xk-1,xk], k = 1,
2, ..., ![]() . Поэтому
. Поэтому
0 < 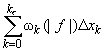 <
<
![]()
![]() k( f )
k( f )![]() xk,
xk,
а поскольку, согласно уже упоминавшемуся
критерию интегрируемости (23.21), для интегрируемой
функции f выполняется условие ![]()
![]()
![]() k( f )
k( f )![]() xk = 0 , то и
xk = 0 , то и ![]()
![]()
![]() k(| f |)
k(| f |)![]() xk= 0 , откуда и
следует интегрируемость функции | f |.
xk= 0 , откуда и
следует интегрируемость функции | f |.
Если теперь ![]() ( f ) =
( f ) = ![]() f(
f(![]() k)
k)![]() xk,
xk, ![]() k
k ![]() [xk-1,xk], k = 1,
2, ...,
[xk-1,xk], k = 1,
2, ..., ![]() , т. е.
, т. е. ![]() ( f )
- интегральная сумма Римана функции f, то
( f )
- интегральная сумма Римана функции f, то
| |
(24.18) |
где в правой части неравенства стоит интегральная сумма Римана функции | f |. Так как
![]()
![]() ( f )
=
( f )
= ![]() f(x)dx,
f(x)dx,
![]()
![]() (| f |) =
(| f |) = ![]() | f(x)|dx ,
| f(x)|dx ,
то, перейдя в неравенстве (24.18) к пределу при |![]() |
|![]() 0,
получим
0,
получим
![]()
![]() f(x)dx
f(x)dx![]() <
< ![]() | f(x)|dx.
| f(x)|dx.
Заметим, что если не предполагать, что a < b (см. п. 23.1), то вместо неравенства (24.16) следует писать
|
(24.19) |
10o. Непрерывность интеграла. Если функция f интегрируема на отрезке [a,b], то функции
| F(x) |
(24.20) |
| G(x) |
(24.21) |
непрерывны на этом отрезке.
Следствие. Если функция f
интегрируема на отрезке [a,b], то
|
(24.22) |
![]() Функция f,
будучи интегрируемой на отрезке [a,b],
ограничена на нем, поэтому существует такая
постоянная c > 0, что для всех x
Функция f,
будучи интегрируемой на отрезке [a,b],
ограничена на нем, поэтому существует такая
постоянная c > 0, что для всех x ![]() [a,b]
выполняется неравенство
[a,b]
выполняется неравенство
| f(x)| < c. |
(24.23) |
Представим интеграл ![]() f(t)dt
в виде суммы (см. (24.3)):
f(t)dt
в виде суммы (см. (24.3)):
|
(24.24) |
(отметим, что это равенство верно как при ![]() x > 0, так и при
x > 0, так и при ![]() x < 0 , лишь бы x
x < 0 , лишь бы x ![]() [a,b] и x +
[a,b] и x +
![]() x
x ![]() [a,b] ). Теперь видно, что
приращение
[a,b] ). Теперь видно, что
приращение ![]() F(x)
функции F(x) (см. (24.20)) можно записать в
виде
F(x)
функции F(x) (см. (24.20)) можно записать в
виде
|
(24.25) |
Поэтому
|![]() F(x)|
=
F(x)|
= ![]()
![]() f(t)dt
f(t)dt![]()
![]()
![]()
![]() | f(t)|dt
| f(t)|dt![]()
![]() c
c![]()
![]() dt
dt![]() = c|x|.
= c|x|.
Отсюда, очевидно, сразу следует, что ![]()
![]() F(x)
= 0, т. е. непрерывность функции F(x).
F(x)
= 0, т. е. непрерывность функции F(x).
Непрерывность функции G(x)
следует из непрерывности функции F(x).
В самом деле, поскольку
![]() f(t)dt
+
f(t)dt
+ ![]() f(t)dt =
f(t)dt = ![]() f(t)dt,
f(t)dt,
т. е. F(x) + G(x) = ![]() f(t)dt, то
f(t)dt, то
G(x) = |
(24.26) |
а так как интеграл ![]() f(t)dt -
постоянная величина, то непрерывность функции F
влечет за собой непрерывность функции G.
f(t)dt -
постоянная величина, то непрерывность функции F
влечет за собой непрерывность функции G. ![]()
Свойство непрерывности
функции F называется непрерывностью
интеграла ![]() f(t)dt
по верхнему пределу интегрирования,
соответственно свойство непрерывности функции G -
непрерывностью интеграла по нижнему пределу
интегрирования.
f(t)dt
по верхнему пределу интегрирования,
соответственно свойство непрерывности функции G -
непрерывностью интеграла по нижнему пределу
интегрирования.
![]() Для того чтобы
убедиться в справедливости равенства (24.22),
выберем какую-либо точку c
Для того чтобы
убедиться в справедливости равенства (24.22),
выберем какую-либо точку c ![]() (a,b), тогда функции
(a,b), тогда функции ![]() f(t)dt и
f(t)dt и ![]() f(t)dt в силу
свойства непрерывны соответственно в точках x = a
и x = b, поэтому при
f(t)dt в силу
свойства непрерывны соответственно в точках x = a
и x = b, поэтому при
0 < ![]() < b - a
будем иметь
< b - a
будем иметь
![]()
![]() f(x)dx
f(x)dx![]()
![]()
![]()
![]() f(x)dx+
f(x)dx+![]() f(x)dx
f(x)dx![]() =
=
= ![]()
![]() f(x)dx +
f(x)dx + ![]()
![]() f(x)dx
f(x)dx![]()
![]() f(x)dx+
f(x)dx+![]() f(x)dx
f(x)dx![]()
![]() f(x)dx.
f(x)dx.
Интегрируемость непрерывных и монотонных функций Оглавление Интегральная теорема о среднем