Определение 2. Для отрезка [a,b] всякая система
Под длиной кривой понимается точная
верхняя грань длин вписанных в эту кривую
ломанных. Сформулируем это определение более
подробно. Введем сначала понятие разбиения
отрезка - понятие, которое будет неоднократно
встречаться в дальнейшем.
Определение 2. Для отрезка [a,b]
всякая система ![]() точек ti,
i = 0, 1, 2, ..., ir, таких, что
точек ti,
i = 0, 1, 2, ..., ir, таких, что
|
![]()
называется его разбиением.
Пусть задана кривая
Г = {r(t); a < t < b}
и пусть ![]() -
некоторое разбиение отрезка [a,b].
Положим
-
некоторое разбиение отрезка [a,b].
Положим
|
(17.18) |
т. е. ![]() - это длина
ломаной с вершинами в точках Mi,
являющихся концами радиус-векторов r(ti),
i = 0, 1, 2, ..., ir, иначе говоря,
ломаной, вписанной в кривую Г (рис. 93).
- это длина
ломаной с вершинами в точках Mi,
являющихся концами радиус-векторов r(ti),
i = 0, 1, 2, ..., ir, иначе говоря,
ломаной, вписанной в кривую Г (рис. 93).
Определение 3. Верхняя грань
длин всевозможных ломаных, вписанных в данную
кривую, называется ее длиной.
Таким образом, длина SГ
кривой Г определяется формулой
|
(17.19) |
где верхняя грань берется по всевозможным
разбиениям ![]() отрезка [a,b].
Очевидно, 0 < SГ < +
отрезка [a,b].
Очевидно, 0 < SГ < +![]() .
.
Если SГ < +![]() , то кривая Г называется спрямляемой.
, то кривая Г называется спрямляемой.
Теорема 1. Если кривая Г = {r(t);
a < t < b}
непрерывно дифференцируема, то она
спрямляема и ее длина SГ
удовлетворяет неравенству
|r(b) - r(a)| < SГ < c(b - a), |
(17.20) |
где
|
(17.21) |
![]() Прежде всего
заметим, что в силу непрерывности на отрезке [a,b]
производной r'(t) числовая
функция |r'(t)| также непрерывна
на этом отрезке, а следовательно, ограничена и
принимает на нем наибольшее значение. Поэтому
существует число
Прежде всего
заметим, что в силу непрерывности на отрезке [a,b]
производной r'(t) числовая
функция |r'(t)| также непрерывна
на этом отрезке, а следовательно, ограничена и
принимает на нем наибольшее значение. Поэтому
существует число ![]() < +
< +![]() .
.
Возьмем какое-либо разбиение ![]() отрезка [a,b].
Тогда, используя очевидное векторное тождество
отрезка [a,b].
Тогда, используя очевидное векторное тождество
|
(17.22) |
и применяя теорему 1 из п. 16.2, получим
|
(17.23) |
где ti-1 < ![]() i < ti, i = 1,
2, ..., ir. Так как
i < ti, i = 1,
2, ..., ir. Так как 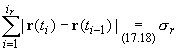 - длина вписанной в кривую Г ломаной,
соответствующей разбиению
- длина вписанной в кривую Г ломаной,
соответствующей разбиению ![]() ,
то из неравенства (17.23) следует, что
,
то из неравенства (17.23) следует, что
|r(b) - r(a)| <
![]() < c(b - a),
< c(b - a),
Перейдя в этом неравенстве к верхней грани по
всевозможным разбиениям ![]() отрезка [a,b], получим, в силу определения
(17.19), неравенство (17.20)
отрезка [a,b], получим, в силу определения
(17.19), неравенство (17.20)
![]()
Поэтому SГ < +![]() , т. е. кривая Г
спрямляема.
, т. е. кривая Г
спрямляема. ![]()
Теорема 2. Если кривая Г = {r(t) = (x(t),
y(t), z(t)); a < t < b}
непрерывно дифференцируема, то переменная
длина дуги s = s(t), отсчитываемая
от начала кривой Г, является возрастающей
непрерывно дифференцируемой функцией параметра t
и
|
(17.24) |
![]() Как и выше, будем через M(t)
обозначать конец радиус-вектора r(t).
Пусть s(t) - длина дуги кривой Г от
точки M(a) до точки M(t), t
Как и выше, будем через M(t)
обозначать конец радиус-вектора r(t).
Пусть s(t) - длина дуги кривой Г от
точки M(a) до точки M(t), t ![]() [a,b], t +
[a,b], t + ![]() t
t ![]() [a,b], и
[a,b], и ![]() s = s(t +
s = s(t + ![]() t) - s(t).
Очевидно, что |
t) - s(t).
Очевидно, что |![]() s|
является длиной дуги с концами в точках M(t)
и M(t +
s|
является длиной дуги с концами в точках M(t)
и M(t + ![]() t).
t).
Поэтому согласно теореме 1
для ![]() r = r(t +
r = r(t + ![]() t) - r(t)
имеет место неравенство
t) - r(t)
имеет место неравенство
| |
(17.25) |
где c - наибольшее значение |r'(t)|
на отрезке с концами в точках t и t + ![]() t. Обозначим через
t. Обозначим через ![]() =
= ![]() (
(![]() t) точку
этого отрезка, в которой
t) точку
этого отрезка, в которой
|r'( |
(17.26) |
Поделим обе части равенства (17.25) на |![]() t|,
t|, ![]() t
t![]() 0:
0:
|
(17.27) |
Функция s = s(t)
возрастает (с увеличением дуги ее длина
возрастает). Поэтому если ![]() t > 0, то
t > 0, то ![]() s > 0, а если
s > 0, а если ![]() t < 0, то
t < 0, то ![]() s < 0 и, следовательно, всегда
s < 0 и, следовательно, всегда ![]() s/
s/![]() t > 0, иначе говоря, |
t > 0, иначе говоря, |![]() s/
s/![]() t| =
t| = ![]() s/
s/![]() t. Таким образом,
неравенство (17.27) можно записать в виде
t. Таким образом,
неравенство (17.27) можно записать в виде
|
(17.28) |
Левая и правая части этого
неравенства имеют при ![]() t
t![]() 0 один и тот же предел, равный |r'(t)|.
В самом деле, в силу определения производной
0 один и тот же предел, равный |r'(t)|.
В самом деле, в силу определения производной
![]()
Из выполнения же условия ![]()
![]() [t,t+
[t,t+![]() t] при
t] при ![]() t > 0 или условия
t > 0 или условия ![]()
![]() [t+
[t+![]() t,
t,![]() t] при
t] при ![]() t < 0 следует, что
t < 0 следует, что
![]()
![]() = t, а так как функция |r'(t)|
непрерывна, то отсюда вытекает, что
= t, а так как функция |r'(t)|
непрерывна, то отсюда вытекает, что ![]() |r'(
|r'(![]() )| = |r'(t)|.
А тогда из неравенства (17.28) получаем, что предел
)| = |r'(t)|.
А тогда из неравенства (17.28) получаем, что предел ![]() (
(![]() s/
s/![]() t) существует и также
равен |r'(t)|. Это означает, что
существует производная s'(t) и что s'(t) = |r'(t)|.
Если r(t) = (x(t), y(t),
z(t)), то r'(t) = (x'(t),
y'(t), z'(t)), а потому
t) существует и также
равен |r'(t)|. Это означает, что
существует производная s'(t) и что s'(t) = |r'(t)|.
Если r(t) = (x(t), y(t),
z(t)), то r'(t) = (x'(t),
y'(t), z'(t)), а потому
s'(t) = |r'(t)|
= [(x'(t))2 + ( y'(t))2 + (z'(t))2]1/2.
|
(17.29) |
Замечание 1. Если длина ![]() дуг кривой Г отсчитывается от ее
конца, то
дуг кривой Г отсчитывается от ее
конца, то ![]() = SГ - s
и, следовательно,
= SГ - s
и, следовательно,
d![]() /ds = -1, поэтому
/ds = -1, поэтому
![]()
Замечание 2. Если непрерывно
дифференцируемая кривая Г = {r(t);
a < t < b} не
имеет особых точек
(r'(t)![]() 0
на отрезке [a,b]), т. е. Г - гладкая
кривая, то в силу теоремы 2 переменная длина
дуги s = s(t), отсчитываемая от
начала M(a) кривой Г, является строго
возрастающей непрерывно дифференцируемой
функцией с производной, положительной во всех
точках отрезка [a,b]: s(t) = |r'(t)| > 0.
0
на отрезке [a,b]), т. е. Г - гладкая
кривая, то в силу теоремы 2 переменная длина
дуги s = s(t), отсчитываемая от
начала M(a) кривой Г, является строго
возрастающей непрерывно дифференцируемой
функцией с производной, положительной во всех
точках отрезка [a,b]: s(t) = |r'(t)| > 0.
А так как s(a) = 0, s(b) = SГ,
то обратная функция t = t(s)
однозначна, строго возрастает, непрерывно
дифференцируема на отрезке [0,SГ] и
|
(17.30) |
Таким образом, для всякой гладкой
кривой ее параметр является строго возрастающей
непрерывно дифференцируемой функцией
переменной длины дуги и производная этой функции
нигде не обращается в нуль.
Следовательно, функция t = t(s)
есть допустимое преобразование параметра в
смысле п. 17.1 и,
следовательно, на гладкой кривой в качестве
параметра можно взять переменную длину ее дуг. Из
сказанного вытекает также, что имеет смысл
производная
|
(17.31) |
Вектор dr/ds только числовым
множителем dt/ds отличается от
касательного вектора dr/dt ![]() 0 и поэтому также
направлен по касательной. Докажем, что вектор dr/ds
является единичным вектором.
0 и поэтому также
направлен по касательной. Докажем, что вектор dr/ds
является единичным вектором.
Теорема 3. Если на кривой Г = {r(s);
0 < s < S}
параметром является длина дуги и кривая
непрерывно дяфференцируема, то
|dr/ds| = 1. |
(17.32) |
![]() Из формулы (17.24) при t
= s имеем
Из формулы (17.24) при t
= s имеем
|dr/ds| = ds/ds =
1. ![]()
|
Поскольку на гладкой кривой можно
взять за параметр длину дуги, то формула (17.32)
имеет место для гладких кривых.
Разъясним геометрический смысл
равенства (17.32).
Отрезок, соединяющий две точки кривой,
называется хордой, стягивающей дугу кривой с
концами в этих точках. Пусть кривая Г гладкая и r(s),
0 < s < S, - ее
векторное представление, в котором в качестве
параметра выбрана переменная длина дуги кривой s
![]() [0,S].
[0,S].
Длина хорды, соединяющей концы
радиус-векторов r(s0) и r(s0 + ![]() s), s0
s), s0 ![]() [0,S], s0 +
[0,S], s0 + ![]() s
s ![]() [0,S], равна длине |
[0,S], равна длине |![]() r| вектора
r| вектора ![]() r = r(s0 +
r = r(s0 + ![]() s) - r(s0)
(рис. 94). В силу равенства (17.32) для предела
отношения |dr|/|ds|
s) - r(s0)
(рис. 94). В силу равенства (17.32) для предела
отношения |dr|/|ds|
при ![]() s
s![]() 0 имеем
0 имеем
|
(17.33) |
т. е. отношение длины хорды к длине стягиваемой
ею дуги стремится к единице, когда ![]() s
s![]() 0.
0.
Замечание 3. Координатами всякого единичного
вектора являются его направляющие косинусы
углов, которые он образует с осями координат.
Поэтому если обозначить через ![]() ,
, ![]() и
и ![]() углы, которые образует с
координатными осями переменных x, y и z
единичный вектор dr/ds, то
углы, которые образует с
координатными осями переменных x, y и z
единичный вектор dr/ds, то
dr/ds = (cos |
(17.34) |
С другой стороны,
dr/ds = (dx/ds, dy/ds, dz/ds). |
(17.35) |
Сравнив формулы (17.34) и (17.35), получим
dx/ds = cos |
(17.36) |
Замечание 4. Если плоская кривая является графиком функции y = f(x), a < x < b, т. е. параметром кривой является переменная x, то x' = 1, и поэтому
ds/dx = (1 + y' 2)1/2.
Замечание 5. Если кривая Г гладкая и в
качестве параметра на ней взята переменная длина
дуги s, 0 < s < S,
то единичный касательный вектор ![]() = dr/ds
является непрерывной функцией переменной s.
= dr/ds
является непрерывной функцией переменной s.
Если какая-то функция является
непрерывной функцией параметра кривой, то будем
говорить, что она непрерывна вдоль кривой. Теперь
можно сказать, что на ориентированной гладкой
кривой имеется непрерывный вдоль нее единичный
касательный вектор. При изменении ориентации
кривой, т. е. при переходе к параметру s* = S - s,
касательный вектор меняет свое направление.
Действительно, поскольку
ds/ds*, то ![]() * =
(dr/ds)( ds/ds*) = -dr/ds
= -
* =
(dr/ds)( ds/ds*) = -dr/ds
= -![]() .
.
Таким образом, ориентации гладкой
кривой однозначным образом соответствует выбор
непрерывного единичного касательного вектора
вдоль кривой ![]() или
или ![]() *. Пусть Г - плоская кривая и на
плоскости фиксирован базис i, j.
В этом случае каждому касательному вектору
*. Пусть Г - плоская кривая и на
плоскости фиксирован базис i, j.
В этом случае каждому касательному вектору ![]() и
и ![]() * соответствует
единственный перпендикулярный к нему единичный
вектор
* соответствует
единственный перпендикулярный к нему единичный
вектор ![]() и соответственно
и соответственно ![]() * (нормаль к кривой) такой, что пары
векторов
* (нормаль к кривой) такой, что пары
векторов ![]() ,
, ![]() и
и ![]() *,
*, ![]() * ориентированы
так же как пара i, j векторов
базиса (т. е. так, что определители
преобразования этих пар положительны). Очевидно,
что
* ориентированы
так же как пара i, j векторов
базиса (т. е. так, что определители
преобразования этих пар положительны). Очевидно,
что ![]() * = -
* = -![]() , и нормали
, и нормали ![]() и
и ![]() * также являются
непрерывными функциями вдоль кривой Г. Из
сказанного ясно, что при фиксированной системе
координат ориентация плоской кривой может быть
задана непрерывной вдоль этой кривой единичной
нормалью.
* также являются
непрерывными функциями вдоль кривой Г. Из
сказанного ясно, что при фиксированной системе
координат ориентация плоской кривой может быть
задана непрерывной вдоль этой кривой единичной
нормалью.
Касательная к кривой Оглавление Определение кривизны и радиуса кривизны кривой