29.1. Определение несобственных интегралов

    Пусть функция f определена на конечном или бесконечном полуинтервале [a,b), - < a < b < +, и для любого числа [a,b) интегрируема на отрезке [a,).
    Определение 1. Функция F() = f(x)dx верхнего предела интегрирования,  a < < b, называется несобственным интегралом и обозначается

f(x)dx.

    Если существует конечный предел f(x)dx, то несобственный интеграл f(x)dx называется сходящимся, а если этот предел не существует, то - расходящимся.
    В случае когда несобственный интеграл сходится, говорят также, что он существует, а если расходится, то не существует.
    Если интеграл f(x)dx сходится, то предел f(x)dx обозначается тем же символом, что и сам интеграл, т. е.

и для краткости также называется несобственным интегралом (иногда - его значением).
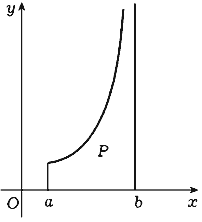
    Подчеркнем, что здесь возможны два случая: когда b - конечное число и когда b равно бесконечности (рис. 119).

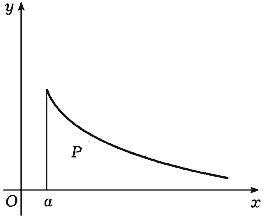Рис. 119

    Если b конечно, а функция f интегрируема на отрезке  [a,b], то в силу непрерывности интеграла (свойство 9 в п. 24.1) предел f(x)dx, a < < b, существует и равен интегралу f(x)dx. Таким образом, интеграл Римана является частным случаем несобственного интеграла.
    При условии конечности b определение 1 содержательно, только если функция f неограничена в любой окрестности точки b (см. рис. 119): если функция f ограничена на полуинтервале  [a,b) и для любого [a,b) она интегрируема по Риману на отрезке [a,], то нетрудно убедиться, что несобственный интеграл f(x)dx существует и совпадает с интегралом Римана функции f, произвольно доопределенной в точке x = b.
    Для отличия интеграла Римана от несобственного интеграла интеграл Римана называют иногда собственным интегралом.
    Геометрический смысл несобственного интеграла f(x)dx от неотрицательной функции f состоит в том, что он, подобно собственному интегралу, равен площади криволинейной трапеции

P = {(x, y):  a < x < b,  0 <  y <  f(x),},

порожденной графиком функции f, причем эта трапеция (как в случае неограниченной функции f и конечного промежутка  [a,b), так и в случае бесконечного промежутка  [a,b)) всегда является (в отличие от того, что имело место для собственного интеграла) неограниченным множеством.
    Если a < c < b, то из равенства

сразу видно, что несобственный интеграл (29.1) существует в том и только том случае, когда существует несобственный интеграл f(x)dx = f(x)dx, причем в случае существования этих интегралов, перейдя в равенстве (29.1) к пределу при b, получим

В этом равенстве и  - несобственные интегралы, а  - собственный интеграл.
    Если функция f определена на полуинтервале (a,b], - < a < b < +, и при любом (a,b] интегрируема по Риману на отрезке [,b], то аналогично формуле (29.1) несобственный интеграл f(x)dx определяется как функция F() = f(x)dx нижнего предела интегрирования, a < < b.
    Если существует конечный предел f(x)dx, то несобственный интеграл называется сходящимся, а если этот предел не существует, то - расходящимся.
    Здесь, как и выше, в случае, когда несобственный интеграл сходится, говорят, что он существует, а когда расходится, что он не существует.
    Если интеграл f(x)dx сходится, то предел f(x)dx обозначается тем же символом, что и сам интеграл, т. е.

и для краткости также называется несобственным интегралом (иногда - его значением).
    Для интеграла (29.4) имеет место свойство, аналогичное свойству (29.3) для интеграла (29.1).
    Если функция f определена на интервале (a,b), - < a < b < +, и c (a,b), то несобственным интегралом f(x)dx называется пара несобственных интегралов f(x)dx,f(x)dx. Если оба эти интеграла сходятся, то интеграл f(x)dx называется сходящимся, а если хотя бы один расходится, то - расходящимся. Если интегралы f(x)dx иf(x)dx сходятся, то их сумма обозначается тем же символом f(x)dx, т. е.

    Из свойства (29.3) и аналогичного свойства для интеграла (29.4) следует, что существование и значение несобственного интеграла f(x)dx не зависят в рассматриваемом случае от выбора точки c (a,b).
    Определим теперь общее понятие несобственного интеграла от функции f по промежутку с концами a и b, - < a < b < +.
    Всякое множество точек X = расширенной числовой прямой называется правильным разбиением промежутка относительно функции f, если:
    1) a = < x₀ < x₁ < ...< x_n  = b;
    2) функция f интегрируема по Риману на любом конечном отрезке, лежащем на промежутке и не содержащем точек множества X.
    Ясно, что на каждом из промежутков (x₀,x₁), (x₁,x₂), ..., (x_n-1,x_n), имеет смысл несобственный интеграл от функции f одного из трех рассмотренных выше типов.
    Совокупность интегралов

называется в этом случае несобственным интегралом f(x)dx .
    Если все интегралы (29.6) сходятся, то интеграл f(x)dx называется сходящимся, а если хотя бы один из них расходится, то - расходящимся.
    В случае когда интеграл f(x)dx сходится, через f(x)dx обозначается и сумма интегралов (29.6), т. е.

f(x)dx f(x)dx,

и эта сумма также называется несобственным интегралом (иногда - его значением).
    Сходимость и расходимость несобственного интеграла, как и его значение, если он сходится, не зависят от выбора правильного разбиения промежутка относительно заданной функции f.
    Заметим, что если к правильному разбиению X промежутка добавить любое конечное множество точек расширенной числовой прямой, принадлежащих этому промежутку, то полученное множество также будет, очевидно, правильным разбиением относительно функции f.
    Перейдем к рассмотрению примеров. Вычислим несобственные интегралы от функции f(x) = , > 0, на полуинтервале (0,1] (где она неограниченна) и на бесконечном промежутке [1,+).
    Примеры.
    1.
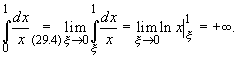
    2. 1,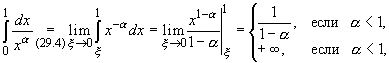

    Обратим внимание на то, что при несобственный интеграл существует, в то время как собственный интеграл заведомо не существует, поскольку функция при любом ее доопределении в точке x = 0 будет неограниченной на отрезке [0,1].
    Этот пример говорит о том, что в случае конечного промежутка понятие несобственного интеграла шире понятия собственного интеграла. В случае же бесконечного промежутка понятия собственного интеграла просто нет.
    Итак, интеграл сходится при < 1 и расходится при > 1 (при < 0 этот интеграл является интегралом Римана).

    3.
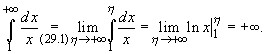
    4. 1,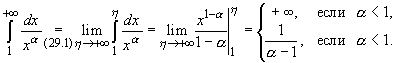 

    Итак, интеграл сходится при > 1 и расходится при < 1.

Теоремы Гульдина. Центры тяжести плоских фигур и их моменты относительно осей    Оглавление  Формулы интегрального исчисления для несобственных интегралов