29.2. Формулы интегрального исчисления для
несобственных интегралов
В силу свойства предела функций и
определения значения несобственного интеграла
как предела функции, являющейся интегралом
Римана с переменным пределом интегрирования, на
собственные интегралы предельным переходом
переносятся многие свойства определенного
интеграла. В дальнейшем в этом параграфе для
простоты в вопросах теории будем рассматривать
случай несобственного интеграла от функций,
определенных на полуинтервале [a,b) и
интегрируемых по Риману на любом отрезке [a,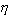 ),
),
-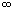 < a <
< a < 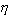 < b < +
< b < +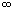 (определение (29.1)),
если, конечно, специально не оговорено что-либо
другое.
(определение (29.1)),
если, конечно, специально не оговорено что-либо
другое.
Аналогичные определения и теоремы
для интегралов (29.4) и (29.5) читатель без труда
сформулирует самостоятельно.
Для общего несобственного интеграла
(29.6) утверждения, аналогичные тем, которые будут
сформулированы ниже для интеграла вида (29.1),
также справедливы и в случае необходимости могут
быть сформулированы читателем.
1o. Формула
Ньютона-Лейбница. Если функция f
непрерывна на промежутке [a,b) и Ф -
какая-либо ее первообразная, то
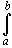 f(x)dx
= Ф(b - 0) - Ф(a). f(x)dx
= Ф(b - 0) - Ф(a).
|
(29.7) |
В этом равенстве либо обе части
одновременно имеют смысл, и тогда они равны, либо
они одновременно не имеют смысла, т. е. стоящие
в них пределы не существуют.
 Справедливость
формулы (29.7) следует из того, что для любого ,
согласно формуле Ньютона-Лейбница для интеграла
Римана (теорема 3 из п. 25.2), имеет место
равенство
Справедливость
формулы (29.7) следует из того, что для любого ,
согласно формуле Ньютона-Лейбница для интеграла
Римана (теорема 3 из п. 25.2), имеет место
равенство
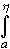 f(x)dx
= Ф( f(x)dx
= Ф(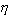 ) - Ф(a). ) - Ф(a).
|
(29.8) |
Из него следует, что предел 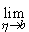
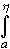 f(x)dx
существует тогда и только тогда, когда
существует предел
f(x)dx
существует тогда и только тогда, когда
существует предел 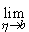 Ф(
Ф(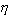 ), причем, если
эти пределы существуют, то, перейдя в равенстве
(29.8) к пределу при
), причем, если
эти пределы существуют, то, перейдя в равенстве
(29.8) к пределу при 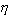
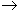 b, получим формулу (29.7).
b, получим формулу (29.7). 
2o. Линейность
интеграла. Если несобственные интегралы 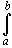 f(x)dx и
f(x)dx и 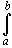 g(x)dx сходятся,
то для любых чисел
g(x)dx сходятся,
то для любых чисел  и
и 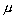 несобственный интеграл
несобственный интеграл 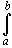 [
[ f(x)
+
f(x)
+ 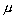 g(x)]dx
также сходится и
g(x)]dx
также сходится и
 Действительно, на основании соответствующих
свойств предела и линейности интеграла Римана
имеем
Действительно, на основании соответствующих
свойств предела и линейности интеграла Римана
имеем
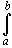 [
[ f(x) +
f(x) + 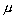 g(x)]dx
g(x)]dx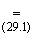
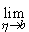
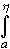 [
[ f(x)
+
f(x)
+ 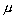 g(x)]dx =
g(x)]dx = 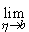
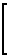

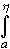 f(x)dx +
f(x)dx + 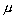
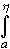 g(x)dx
g(x)dx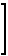 =
=
= 
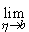
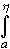 f(x)dx
+
f(x)dx
+ 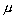
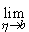
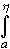 g(x)dx
g(x)dx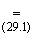

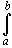 f(x)dx +
f(x)dx + 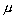
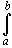 g(x)dx.
g(x)dx.

3o. Интегрирование
неравенств. Если интегралы 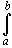 f(x)dx и
f(x)dx и 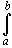 g(x)dx сходятся и для всех x
g(x)dx сходятся и для всех x
 [a,b)
выполняется неравенство f(x) < g(x),
то
[a,b)
выполняется неравенство f(x) < g(x),
то
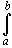 f(x)dx
< f(x)dx
< 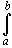 g(x)dx. g(x)dx.
|
(29.10) |
 В силу
соответствующего свойства интеграла Римана (см.
следствие свойства 7o
в п. 24.1) для любого выполняется неравенство
В силу
соответствующего свойства интеграла Римана (см.
следствие свойства 7o
в п. 24.1) для любого выполняется неравенство
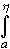 f(x)dx
<
f(x)dx
< 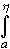 g(x)dx.
g(x)dx.
Перейдя в нем к пределу при 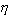
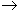 b, получим
неравенство (29.10).
b, получим
неравенство (29.10). 
Аналогичным образом, исходя из
соответствующих свойств интеграла Римана, с
помощью предельного перехода доказываются и
следующие два свойства несобственных интегралов
(проведение доказательств которых
предоставляется читателю).
4o. Правило замены
переменной. Если функция f(x)
непрерывна на полуинтервале 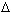 x = [a,b), функция
x = [a,b), функция
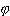 (t) непрерывно
дифференцируема на полуинтервале
(t) непрерывно
дифференцируема на полуинтервале  t = [
t = [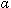 ,
,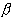 ), -
), -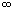 < a <
< a < 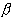 < +
< +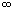 , и выполняются условия
, и выполняются условия
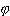 (
( t)
t) 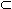
 x,
a =
x,
a = 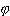 (
(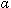 ), a =
), a = 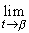
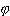 (t),
(t),
то
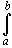 f(x)dx =
f(x)dx =
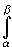 f(
f(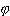 (t))
(t))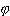 '(t)dt,
'(t)dt,
причем из существования интеграла, стоящего
слева в этом равенстве, следует
существование интеграла, стоящего справа.
Если функция 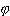 такова, что обратная функция
такова, что обратная функция 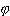 -1 однозначна и
удовлетворяет условиям, аналогичным условиям,
наложенным на функцию
-1 однозначна и
удовлетворяет условиям, аналогичным условиям,
наложенным на функцию 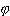 ,
и, следовательно, в интеграле, стоящем в правой
части равенства (29.11), можно сделать замену
переменной t =
,
и, следовательно, в интеграле, стоящем в правой
части равенства (29.11), можно сделать замену
переменной t = 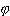 -1(x),
то оба интеграла в этом равенстве сходятся или
расходятся одновременно.
-1(x),
то оба интеграла в этом равенстве сходятся или
расходятся одновременно.
С помощью замены переменной из условий
сходимости интегралов, рассмотренных в
примерах 1 и 2 п. 29.1, следует, что интегралы
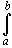
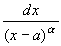 и
и 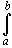
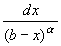 , -
, -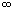 < a < b <
+
< a < b <
+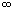 , сходятся при
, сходятся при 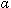 < 1 и расходятся при
< 1 и расходятся при 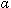 > 1. В самом деле, первый
интеграл с помощью замены переменной t = x - a,
а второй с помощью t = b - x
приводятся к интегралу
> 1. В самом деле, первый
интеграл с помощью замены переменной t = x - a,
а второй с помощью t = b - x
приводятся к интегралу 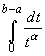 .
.
5o. Правило
интегрирования по частям. Если функции u
и v непрерывны на промежутке [a,b),
а их производные кусочно непрерывны на любом
отрезке [a,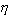 ), a
<
), a
< 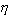 < b, то
< b, то
При этом из существования любых двух из
следующих трех пределов:
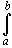 udv =
udv = 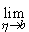
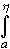 udv,
udv, 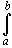 vdu =
vdu = 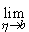
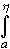 vdu,
vdu,
uv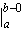 =
= 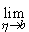 u(
u(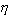 )v(
)v(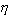 ) - u(a)v(a)
) - u(a)v(a)
следует существование оставшегося.
Замечание. Отметим, что не все свойства
интеграла Римана переносятся на несобственные
интегралы. Например, интеграл от произведения
двух функций может расходится в случае, когда
интеграл от каждого из сомножителей сходится:
если f(x) = x-1/2 , то
интеграл 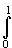 f(x)dx
=
f(x)dx
= 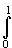 x-1/2dx
сходится, а интеграл
x-1/2dx
сходится, а интеграл
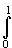 f2(x)dx
=
f2(x)dx
= 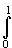 x-1dx
расходится.
x-1dx
расходится.
Примеры.
1. Посредством замены переменной x = 1/t
вычислим интеграл
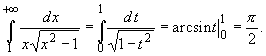
2. Вычислим интеграл 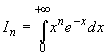 , n = 0,
1, 2, ... Проинтегрировав по частям при n > 0,
будем иметь
, n = 0,
1, 2, ... Проинтегрировав по частям при n > 0,
будем иметь
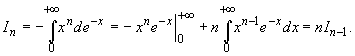
|
(29.13) |
Поскольку 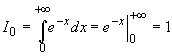 , то,
применив последовательно рекуррентную формулу
(29.13), получим
, то,
применив последовательно рекуррентную формулу
(29.13), получим
In = nIn-1 = n(n - 1)In-1
= n!I0 = n!.
Определение несобственных
интегралов Оглавление Несобственные интегралы от
неотрицательных функций
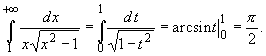
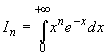 , n = 0,
1, 2, ... Проинтегрировав по частям при n > 0,
будем иметь
, n = 0,
1, 2, ... Проинтегрировав по частям при n > 0,
будем иметь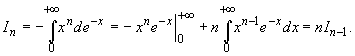
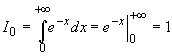 , то,
применив последовательно рекуррентную формулу
(29.13), получим
, то,
применив последовательно рекуррентную формулу
(29.13), получим