29.3. Несобственные интегралы от неотрицательных функций

    Установим признаки сходимости для несобственных интегралов от неотрицательных функций.
    Лемма1. Если функция f неотрицательна на полуинтервале [a,b), то для сходимости интеграла f(x)dx необходимо и достаточно, чтобы множество всех интегралов f(x)dx, [a,b), было ограничено сверху, т. е. чтобы существовала такая постоянная c > 0, что для всех [a,b) выполнялось бы неравенство

Положим

Если a < < ' < b, то

f(') = f(x)dx = f(x)dx + f(x)dx > f(x)dx = (),

ибо в силу неотрицательности функции f имеет место неравенство f(x)dx > 0, т. е. функция () возрастает на полуинтервале [a,b). Существование несобственного интеграла f(x)dx означает существование конечного предела

() = f(x)dx,

что имеет место тогда и только тогда, когда функция ограничена сверху (см. теорему 4 в п. 6.11), а это в силу (29.15) равносильно условию (29.14). 
    Замечание. При доказательстве леммы 1 было показано, что в случае неотрицательности функции f функция (см. (29.15)) возрастает на [a,b) и, следовательно, всегда имеет при конечный или бесконечный, равный +, предел в зависимости от того, ограничена она или нет. Если функция неограничена на [a,b), то

f(x)dx () =  +,

и в этом случае пишут

f(x)dx = +

(как мы уже и поступали в примерах п. 29.1).

    Теорема1 (признак сравнения). Пусть

    Тогда:
    1) если интеграл f(x)dx сходится, то сходится и интеграл g(x)dx;
    2) если интеграл g(x)dx расходится, то расходится и интеграл f(x)dx.
    Следствие 1. Пусть функции f и g неотрицательны на промежутке [a,b), g(x)0 при всех x [a,b) и существует конечный или бесконечный предел

    Тогда:
    1) если интеграл g(x)dx сходится и 0 < k < +, то и интеграл f(x)dx сходится;
    2) если интеграл g(x)dx расходится и 0 < k < +, то и интеграл f(x)dx расходится.
    Следствие 2. Если функции f(x) и g(x) эквивалентны при xb, т. е. f(x) = (x)g(x), a < x < b, то интегралы f(x)dx и g(x)dx одновременно сходятся или расходятся.
    Докажем теорему. Для любого [a,b) в силу неравенства (29.16) имеем

g(x)dx < f(x)dx.

Поэтому если интеграл f(x)dx сходится и, следовательно, согласно лемме 1 ограничен сверху интеграл
f(x)dx, то будет ограничен сверху и интеграл g(x)dx, откуда, согласно той же лемме, интеграл g(x)dx сходится.
    Если же расходится интеграл g(x)dx , то в силу уже доказанного интеграл f(x)dx не может сходиться, так как тогда бы сходился и интеграл g(x)dx, a это противоречит условию. Таким образом, интеграл
f(x)dx расходится. 

    Докажем теперь следствие 1.
    Пусть выполняется условие (29.17) и 0 < k < +. Из того, что k является пределом функции при
xb, и из неравенства k < k + 1 следует существование такого [a,b), что если   < x < b, то
< k + 1 , т. е.

Если сходится несобственный интеграл g(x)dx, то сходится интеграл (k + 1)g(x)dx (см. (29.3) и (29.9)); следовательно, в силу неравенства (29.18) интеграл g(x)dx , а поэтому и интеграл f(x)dx сходятся.
    Пусть теперь условие (29.17) выполняется при 0 < k < +. Тогда зафиксируем произвольно такое k', что 0 < k' < k. Из того, что k является пределом функции при xb, и из неравенства k' < k следует существование такого [a,b), что для всех выполняется неравенство > k', т. е. неравенство

f(x) > k'g(x).

Отсюда в силу расходимости интеграла g(x)dx следует расходимость интеграла k'g(x)dx, а следовательно, по теореме 1 и расходимость интеграла f(x)dx. 

    Докажем теперь следствие 2.
Из условия (x) следует, что существует такое число c, a < c < b, что при c < x < b выполняется неравенство 1/2 < (x) < 3/2. А так как f(x) = (x)g(x), то

g(x) < f(x) < g(x).

    Отсюда в силу теоремы и следует, что интегралы f(x)dx и g(x)dxодновременно сходятся или расходятся.
     При применении признака сходимости для исследования интеграла обычно начинают со сравнения подынтегральной функции с функциями

,   ,   ,

сходимость интегралов от которых уже известна (примеры п. 29.1 и п. 29.2).
    Примеры.
    1. Выясним, сходится ли интеграл

Имеем f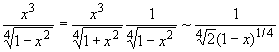(x) = =  , x1, а так как интеграл сходится, то сходится и интеграл (29.19).
    2. Исследуем интеграл

Для любого > 0, применив правило Лопиталя, получим

= = - = 0,

в частности, это равенство имеет место при 0 < < 1. Но при интеграл сходится, следовательно, сходится и интеграл (29.20).
    3. Рассмотрим интеграл

Поскольку ln x = ln [1 + (x - 1)] ~ x - 1 при x1и интеграл расходится, то расходится и интеграл (29.21).
    4. Рассмотрим на бесконечном промежутке (0,+) интеграл

Заметим, что

= = 0

(в этом легко можно убедиться по правилу Лопиталя) и что интеграл e^-x/2dx , очевидно, сходится:

e^-x/2dx = -2e^-x/2= 2.

Отсюда в силу следствия теоремы 1 при f(x) = xⁿe^-x и g(x) = e^-x/2 вытекает, что интеграл (29.22) сходится.

Формулы интегрального счисления для несобственных интегралов Оглавление  Критерий Коши