29.4. Критерий Коши

    Теорема 2 (критерий Коши сходимости интеграла). Несобственный интеграл f(x)dx сходится тогда и только тогда, когда для любого > 0 существует такое , что для всех ' и ", удовлетворяющих условию

выполняется неравенство

(рис.120 и рис.121).

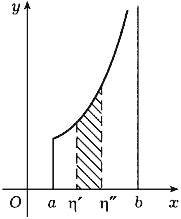Рис. 120

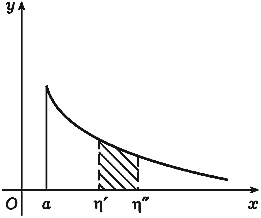Рис. 121

    Если положить

то сходимость интеграла f(x)dx будет означать существование конечного предела функции () при b. Согласно критерию Коши существования предела функции (п. 6.12) для существования указанного предела необходимо и достаточно, чтобы для любого > 0 нашлось такое , что если < ' < b, < "< b, то

Так как

(') - (") f(x)dx - f(x)dx = f(x)dx,

то неравенство (29.24) совпадает с неравенством (29.26). 

Несобственные интегралы от неотрицательных функций  Оглавление   Абсолютно сходящиеся интегралы