31.1. Сходимость функциональных последовательностей и рядов

    Пусть на некотором множестве X (произвольной природы) задана последовательность функций

принимающих числовые значения (вообще говоря, комплексные, в частности, только действительные). Элементы множества X будем называть точками.
    Последовательность (31.1) называется ограниченной на множестве X, если существует такое число c > 0, что для всех n = 1, 2, ... и всех точек x X выполняется неравенство

| f_n(x)| < c.

    Последовательность (31.1) называется сходящейся на множестве X, если при любом фиксированном
x X числовая последовательность {f_n(x)} сходится.
    Если последовательность (31.1) сходится на множестве X, то функция f, определенная при каждом x X равенством

f(x) f_n(x),

называется пределом последовательности (31.1).
    Пусть на множестве X задана последовательность числовых функций u_n(x), n = 1, 2, ... Множество всех числовых рядов u_n(x) , в каждом из которых точка x X произвольно фиксирована, называется  рядом

на множестве X, а функции u_n(x), n = 1, 2, ..., - его членами.
    Аналогично случаю числовых рядов сумма

s_n(x) = u_k(x),      x X,

называется частичной суммой ряда (31.2) n-го порядка, а ряд u_n+k - его n-м остатком.
    Ряд (31.2) называется сходящимся на множестве X, если последовательность {s_n(x)} его частичных сумм сходится на этом множестве. При этом предел частичных сумм

s_n(x) = s(x),     x X,

называется суммой ряда (31.2). В этом случае пишут

s(x) = u_n(x)

и говорят, что функция s(x) раскладывается в ряд (31.2).
    Если ряд (31.2) при любом фиксированном x X сходится абсолютно, то он называется абсолютно сходящимся на множестве X.
    Примеры.
    1. Рассмотрим ряд, членами которого являются функции

u_n(z) = zⁿ/n!,      n = 0, 1, 2, ...,

определенные на комплексной плоскости C, т. е. ряд

Исследуем абсолютную сходимость этого ряда при фиксированном z с помощью признака Даламбера:

|u_n+1(z)|/|u_n(z)| = |z|/(n + 1) = 0.

Таким образом, при любом z C ряд (31.3) абсолютно, а следовательно, и просто сходится; иначе говоря, ряд (31.3) сходится, и притом абсолютно, на всей комплексной плоскости.
    2. Рассмотрим ряд

При x = 0 все его члены обращаются в нуль и, следовательно, его сумма s(x) также равна нулю:

При x 0 ряд (31.4) представляет собой сумму членов бесконечной геометрической прогрессии со знаменателем

q = 1/(1+x²),   0 < q < 1,

и поэтому

    Из формул (31.5) и (31.6) следует, что ряд (31.4) сходится на всей числовой оси и его сумма

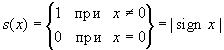
оказывается разрывной в точке x = 0 функцией (см. рис. 60), хотя все его члены, очевидно, непрерывны на всей числовой оси.
    Этот пример показывает, что сумма сходящегося и даже абсолютно сходящегося на некотором множестве ряда (члены ряда (31.4) неотрицательны, и потому ясно, что он абсолютно сходится), все члены которого непрерывны, может оказаться разрывной функцией. Таким образом, на сходящиеся и даже на абсолютно сходящиеся ряды функций не переносится свойство конечных сумм: сумма конечной совокупности непрерывных на некотором множестве функций также непрерывна на нем. Для того чтобы описать ряды функций, на которые переносится это свойство, введем понятие равномерно сходящихся рядов.

Суммирование рядов методом средних арифметических  Оглавление  Равномерная сходимость функциональных последовательностей и рядов