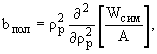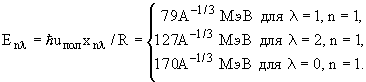5.3. Двухкомпонентная модель
ядерной жидкости
|
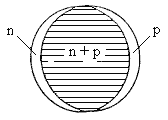 Рис. 5.8. Нейтрон-протонные
поляризационные колебания |
Мы рассмотрели ряд
коллективных степеней свободы ядра, связанных с
колебаниями или с постоянной деформацией формы
поверхности ядра. Однако, это не единственный вид
коллективных движений, который может возникать в
ядре. Любое нарушение равновесного состояния
ядерного вещества вызовет коллективные
колебания возле положения равновесия.
Поверхность ядра и его плотность могут быть
фиксированны, но если ядро поляризуется
(например, под действием падающей
электромагнитной волны) так, что центр тяжести
протонов сместится относительно центра тяжести
нейтронов (см. рис. 5.8), то возникнут
нейтрон-протонные поляризационные колебания
около равновесного распределения протонов и
нейтронов в ядре. Могут быть также
поляризационные колебания, связанные с
возмущением ориентации спинов нуклонов и т.д.
В данном разделе мы опишем модель
двухкомпонентной ядерной жидкости, позволяющую
рассчитать собственные энергии
нейтрон-протонных поляризационных колебаний. В
этой модели нейтроны и протоны рассматриваются
как две взаимопроникающие сжимаемые жидкости,
находящиеся внутри фиксированной ядерной
поверхности. В основном состоянии обе жидкости
равномерно распределены по объему ядра, так как
ядерные силы благоприятствуют однородному
перемешиванию нейтронов и протонов.
Электромагнитное поле возмущает это равновесное
распределение, поэтому при поглощении
γ-кванта возникают колебания плотностей
нейтронной и протонной жидкости
(поляризационные колебания), которые на
эксперименте проявляются как широкие пики
(гигантские резонансы) в сечениях фотоядерных
реакций.
Нейтрон-протонные поляризационные
колебания можно трактовать, как колебания
сжатия-расширения нейтронной и протонной
жидкостей, которые колеблются в противофазе, так
что общая ядерная плотность
ρ(r,t) = ρp(r,t) + ρn(r,t) = ρ0 |
(5.13) |
остается постоянной в любой точке ядра (здесь ρp(r,t) -
плотность протонной жидкости, ρn(r,t) - плотность
нейтронной жидкости и r0 - константа,
характеризующая полную плотность).
Колебания протонной (или нейтронной)
плотностей удовлетворяют обычному волновому
уравнению гидродинамики:
где uпол - скорость
распространения поляризационных колебаний в
среде. Временная зависимость для гармонических
колебаний дается множителем exp(iωt), поэтому уравнение (5.14) сводится к
уравнению Гельмгольца:
Δρp(r) + k2ρp(r) = 0, |
(5.15) |
где
k = ω/uпол = E/( uпол), uпол), |
(5.16) |
k - волновой вектор, ω - частота и E - энергия поляризационных
колебаний.
Скорость распространения
поляризационных волн равна
uпол = (bпол/m)1/2
, |
(5.17) |
где m - масса нуклона,
- aналог коэффициента сжимаемости среды для
поляризационных волн и Wсим -
энергия симметрии ядра. Мы будем предполагать,
что поляризация среды происходит в каждой точке
объема ядра. В этом случае энергия симметрии
может быть записана в виде (ср. с
полуэмпирической формулой Вейцзеккера):
Из (5.18) и (5.19) находим
где  4 4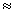 100 МэВ (см. (3.7)) 100 МэВ (см. (3.7))
Мы будем считать, что ядро имеет
фиксированную сферическую форму. Это
предполагает отсутствие потока нуклонов через
поверхность ядра наружу. Откуда следует
граничное условие
где R = r0A-1/3 - радиус ядра.
Общее решение уравнения (5.15)
имеет вид
где 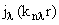 -
сферические функции Бесселя, -
сферические функции Бесселя, 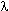 = 0, 1, 2, ... -
характеризует угловой момент колебаний и = 0, 1, 2, ... -
характеризует угловой момент колебаний и
 = - = -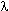 , - , -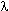 +1, ... , +1, ... , 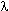 -1, -1, 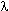 - проекцию углового момента на ось
квантования z. - проекцию углового момента на ось
квантования z.
Собственные значения волнового
вектора 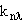 находятся
из граничного условия (5.21), что приводит к задаче
отыскания нулей производной функции Бесселя: находятся
из граничного условия (5.21), что приводит к задаче
отыскания нулей производной функции Бесселя:
Квантовое число n = 1, 2, ... нумерует собственные
значения волнового вектора, отвечающие одному и
тому же значению 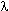 , в порядке
их возрастания. В таблице 5.2 приведены несколько
первых нулей производных , в порядке
их возрастания. В таблице 5.2 приведены несколько
первых нулей производных 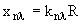 функций Бесселя для функций Бесселя для 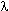 = 0, 1, 2, 3, 4. = 0, 1, 2, 3, 4.
Таблица 5.2
Нули 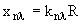 производных
функций Бесселя производных
функций Бесселя |
n\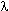 |
0 |
1 |
2 |
3 |
4 |
| 1 |
4.49 |
2.08 |
3.34 |
4.51 |
5.64 |
| 2 |
7.72 |
5.94 |
7.29 |
8.58 |
9.84 |
| 3 |
10.90 |
9.21 |
10.61 |
11.97 |
13.30 |
| 4 |
14.07 |
12.40 |
13.85 |
15.24 |
16.61 |
С помощью формул (5.16), (5.17),
(5.20) и данных таблицы 5.2
можно оценить энергии наиболее низких
поляризационных мод:
Здесь мы приняли bпол = 50 МэВ и R =
1,2A1/3 ферми.
Как видно из (5.24) и таблицы
5.2, наименьшую собственную энергию имеет
дипольная поляризационная мода первого порядка (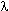 = 1, n = 1). Все остальные
поляризационные моды - квадрупольная ( = 1, n = 1). Все остальные
поляризационные моды - квадрупольная (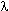 = 2), монопольная ( = 2), монопольная (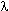 = 0),
октупольная ( = 0),
октупольная (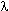 = 3) и т.д. располагаются
значительно выше по шкале энергий. Если оценить
энергию дипольных колебаний по формуле (5.24) для
ядра с массовым числом A = 100, то получится
значение = 3) и т.д. располагаются
значительно выше по шкале энергий. Если оценить
энергию дипольных колебаний по формуле (5.24) для
ядра с массовым числом A = 100, то получится
значение 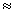 17 МэВ.
Коллективные колебания с такой большой энергией
могут существовать только очень короткое время,
так как они быстро затухают, передовая свою
энергию другим степеням свободы ядра (в том числе
одночастичным, что заканчивается испусканием
нуклонов из ядра). Но чем меньше время жизни t
состояния, тем больше, согласно принципу
неопределенности, его ширина: 17 МэВ.
Коллективные колебания с такой большой энергией
могут существовать только очень короткое время,
так как они быстро затухают, передовая свою
энергию другим степеням свободы ядра (в том числе
одночастичным, что заканчивается испусканием
нуклонов из ядра). Но чем меньше время жизни t
состояния, тем больше, согласно принципу
неопределенности, его ширина:  E ~ E ~  / / .
Поэтому на эксперименте нейтрон-протонные
поляризационные колебания наблюдаются в виде
широких пиков - так называемых гигантских
резонансов. Это иллюстрирует рис. 5.9,
где виден широкий максимум в сечении
фотопоглощения на ядре 197Au, обусловленный
дипольным гигантским резонансом. Энергия
экспериментального пика .
Поэтому на эксперименте нейтрон-протонные
поляризационные колебания наблюдаются в виде
широких пиков - так называемых гигантских
резонансов. Это иллюстрирует рис. 5.9,
где виден широкий максимум в сечении
фотопоглощения на ядре 197Au, обусловленный
дипольным гигантским резонансом. Энергия
экспериментального пика 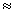 13,5 МэВ хорошо
согласуется с оценкой 13.6 МэВ, даваемой формулой (5.24). 13,5 МэВ хорошо
согласуется с оценкой 13.6 МэВ, даваемой формулой (5.24).
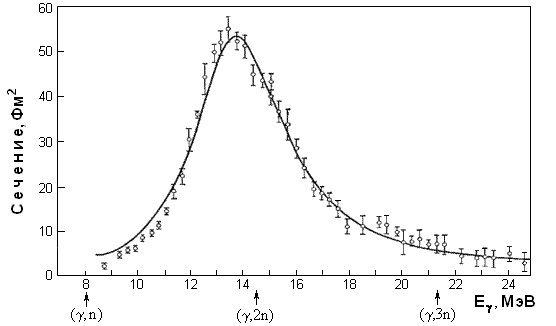
Рис. 5.9. Сечение фотопоглощения для ядра 197Au.
Сплошная кривая - апроксимация
экспериментальных данных по теоретической
резонансной формуле.
|
|