Пусть функции f и g заданы на множестве X и x0 - конечная или бесконечная удаленная точка прикосновения этого множества. При этом возможны случаи, когда x0
Будем предполагать, что существуют такие окрестность U = U(x0) точки x0 и функция
X
Как известно, сумма, разность и
произведение бесконечно малых являются
бесконечно малыми. Частное же бесконечно малых
может быть и не бесконечно малой, однако
отношение бесконечно малых позволяет сравнивать
их "по порядку убывания". Аналогично можно
сравнивать "по порядку роста" бесконечно
большие. Перейдем к точным определениям.
Пусть функции f и g заданы на
множестве X и x0 - конечная или
бесконечная удаленная точка прикосновения этого
множества. При этом возможны случаи, когда x0
![]() X и когда x0
X и когда x0
![]() X.
X.
Будем предполагать, что существуют
такие окрестность U = U(x0)
точки x0 и функция ![]() , заданная на
, заданная на
X ![]() U, что
для всех x
U, что
для всех x ![]() X
X
![]() U выполняется
равенство
U выполняется
равенство
f(x) = |
(9.18) |
В частности, если функции f и g
заданы в точке x0, то и функция ![]() задана в этой точке, а
если f и g не заданы в ней, то не задана в
ней и функция
задана в этой точке, а
если f и g не заданы в ней, то не задана в
ней и функция ![]() .
.
Определение 1. Функция f
называется функцией ограниченной относительно
функции g в окрестности точки x0,
если функция ![]() ограниченна.
ограниченна.
В этом случае существует такая
постоянная c > 0, что для всех x ![]() X
X ![]() U выполняется неравенство
U выполняется неравенство
| |
(9.19) |
а следовательно, и неравенство
| f(x)| |
< |
c|g(x)|. |
(9.20) |
(9.18) |
Условие (9.20) равносильно условиям (9.18) и (9.19). Действительно, если выполняется условие (9.20), то при
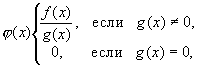
выполняются условия (9.18) и (9.19). Если функция f ограничена относительно функции g в окрестности точки x0, то пишут
f = O(g), x |
(9.21) |
(читается: f есть "O большое" от g).
Определение 2. Функция f
называется функцией того же порядка при x![]() x0, что и функция g,
если существуют такие постоянные c1 > 0
и c2 > 0, что для всех x
x0, что и функция g,
если существуют такие постоянные c1 > 0
и c2 > 0, что для всех x ![]() X
X ![]() U выполняется неравенство
U выполняется неравенство
c1 < | |
(9.22) |
В этом случае для всех x ![]() X
X ![]() U выполняется неравенство
U выполняется неравенство
c1|g(x)| < | f(x)| < c2|g(x)|. |
(9.23) |
Если функция f того же порядка
при x![]() x0, что и
функция g, то пишут f
x0, что и
функция g, то пишут f![]() g, x
g, x![]() x0.
x0.
Очевидно, что функция f того же
порядка при x![]() x0, что
и функция g, тогда и только тогда, когда f =O(g)
и g =O( f), x
x0, что
и функция g, тогда и только тогда, когда f =O(g)
и g =O( f), x![]() x0.
x0.
Определение 3. Функция f
называется бесконечно малой относительно
функции g при x![]() x0,
если функция
x0,
если функция ![]() бесконечно малая при x
бесконечно малая при x![]() x0,
т. е. если
x0,
т. е. если
|
(9.24) |
В этом случае пишут
f =o(g). |
(9.25) |
(читается: f есть "o малое" от g
при x![]() x0).
x0).
Определение 4. Функция f
называется эквивалентной функции g
(или асимптотически равной ей) при
x![]() x0, если
x0, если
|
(9.26) |
В этом случае пишут
f ~ g, x![]() x0.
x0.
Замечание 1. Если x0
![]() X, то, как
известно (см. п. 6.2), из
существования предела
X, то, как
известно (см. п. 6.2), из
существования предела ![]()
![]() (x) следует, что
(x) следует, что
![]()
![]() (x) =
(x) = ![]()
![]() (x0). Поэтому в
случае (9.24) имеем
(x0). Поэтому в
случае (9.24) имеем ![]() (x0)
= 0, а в случае (9.26) -
(x0)
= 0, а в случае (9.26) - ![]() (x0)
= 1.
(x0)
= 1.
Если f =o(g), x![]() x0 и
x0 и ![]() g(x) = 0, то функция f
называется бесконечно малой более высокого
порядка, чем бесконечно малая g. В
случае f =o(gn), x
g(x) = 0, то функция f
называется бесконечно малой более высокого
порядка, чем бесконечно малая g. В
случае f =o(gn), x![]() x0, бесконечно малую f
называют бесконечно малой порядка n
относительно бесконечно малой g.
x0, бесконечно малую f
называют бесконечно малой порядка n
относительно бесконечно малой g.
Замечание 2. Если в условиях
определений 3 или 4 функция g не обращается в
нуль на множестве
x ![]() X
X ![]() U и x0
U и x0 ![]() X, то условие (9.24)
можно записать в виде
X, то условие (9.24)
можно записать в виде
|
(9.27) |
а условие (9.26) - в виде
|
(9.28) |
Замечание 3. Если x0
![]() X, и
существует конечный предел
X, и
существует конечный предел
|
(9.29) |
то функция f(x)/g(x)
ограничена на пересечении некоторой окрестности
U(x0) точки x0 с
множеством X (см. свойство 1o
пределов функций в п. 6.7), т. е. существует
такая постоянная c > 0, что для всех x
![]() X
X ![]() U выполняется
неравенство | f(x)/g(x)| < c,
т. е.
U выполняется
неравенство | f(x)/g(x)| < c,
т. е.
| f(x)| < c|g(x)|,
откуда следует, что при выполнении условия (9.29) имеет место соотношение
f(x) = O(g(x)),
x![]() x0.
x0.
Замечание 4. В определениях
1-4 функции f и g могут быть
последовательностями f = {xn},
g = {yn}, и, таким образом,
указанные определения содержат в себе
определения следующих понятий:
а) последовательности, ограниченной
относительно другой последовательности: xn = O( yn),
n![]()
![]()
б) последовательностей одного порядка:
xn ~ yn, n![]()
![]() ;
;
в) асимптотически равных
последовательностей: xn ![]() yn, n
yn, n![]()
![]() ;
;
г) последовательности, бесконечно
малой по сравнению с другой последовательностью:
xn = o( yn), n![]()
![]() .
.
Примеры. 1. sin 2x = O(x),
x![]() 0, ибо
0, ибо
|sin 2x| < |2x|. |
(9.30) |
Верно и соотношение x = O(sin 2x),
x![]() 0, ибо существует
конечный предел
0, ибо существует
конечный предел ![]() (x/sin 2x)
= 1/2, и, следовательно, функция x/sin 2x
ограничена в некоторой окрестности U(0) точки
x = 0 (см. свойство 1o
пределов функций в п. 6.7). Иначе говоря,
существует такая постоянная c > 0, что
для всех x
(x/sin 2x)
= 1/2, и, следовательно, функция x/sin 2x
ограничена в некоторой окрестности U(0) точки
x = 0 (см. свойство 1o
пределов функций в п. 6.7). Иначе говоря,
существует такая постоянная c > 0, что
для всех x ![]() U(0)
выполняется неравенство |x/sin 2x| < c,
x
U(0)
выполняется неравенство |x/sin 2x| < c,
x![]() 0, поэтому
0, поэтому
|x| < c|sin 2x|,
x |
(9.31) |
Из (9.30) и (9.31) следует, что при x![]() 0 функции y = x и y = sin 2x
одного порядка:
0 функции y = x и y = sin 2x
одного порядка:
sin 2x![]() x,
x
x,
x![]() 0.
0.
2. x3 = o(x2),
x![]() 0, ибо x3 = x2
0, ибо x3 = x2![]() x и
x и ![]() x = 0.
x = 0.
3. x2 = o(x3),
x![]()
![]() , ибо x2 = (1/x)
, ибо x2 = (1/x)![]() x и
x и ![]() (1/x) = 0.
(1/x) = 0.
4. Поскольку ![]() [(sin x)/x],
то функции y = x и y = sin x
эквивалентны при x
[(sin x)/x],
то функции y = x и y = sin x
эквивалентны при x![]() 0:
0:
sin x ~ x, x![]() 0.
0.
Замечание 5. Символы O(g)
и o(g) по существу обозначают целые
классы функций, обладающих по сравнению с данной
функцией определенным свойством, поэтому
равенства типа f(x) = O(g(x))
и f(x) = o(g(x)), x![]() x0, следует читать только
слева направо, например, x2 = o(x),
x
x0, следует читать только
слева направо, например, x2 = o(x),
x![]() 0. Здесь верно то, что
функция y = x2 является при x
0. Здесь верно то, что
функция y = x2 является при x![]() 0 бесконечно малой по сравнению
с функцией y = x, но не всякая
функция, бесконечно малая по сравнению с
функцией y = x, является функцией y = x2.
Равенства с символами O и o не обладают и
рядом других свойств равенств, например,
свойством транзитивности:
0 бесконечно малой по сравнению
с функцией y = x, но не всякая
функция, бесконечно малая по сравнению с
функцией y = x, является функцией y = x2.
Равенства с символами O и o не обладают и
рядом других свойств равенств, например,
свойством транзитивности:
x2 = o(x),
x3 = o(x), x![]() 0,
0,
но x2 ![]() x3.
x3.