26.2. Формула интегрирования по частям

    Теорема 2. Если функции u(x) и v(x) непрерывны вместе со своими производными на отрезке [a,b], то

    Формула (26.2) называется формулой интегрирования по частям  для определенного интеграла.
Имеем

Все интегралы в (26.3) существуют, поскольку подынтегральные
функции непрерывны. Для интеграла в левой части равенства, согласно формуле Ньютона-Лейбница, имеем

(uv)' dx = uv .

Подставив выражение, стоящее в правой части последнего равенства, в (26.3), получим

udv + vdu = uv .

что равносильно (26.2). 

    Замечание. Можно доказать, что формула интегрирования по частям (26.2) остается верной и в том случае, когда функции u и v непрерывны, а их производные кусочно непрерывны (см. п. 24.1).
    Примеры.
    1. Применим формулу интегрирования по частям для вычисления интеграла ln x dx:

ln x dx = x ln x - dx = 2 ln 2 - 1.

    2. Приведем пример интеграла, при вычислении которого применим и замену переменной, и интегрирование по частям. Вычислим интеграл .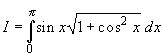
    Сделав сначала замену переменной t = cos x, а затем проинтегрировав по частям, получим

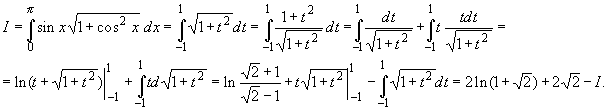
Из получившегося относительно I уравнения находим

I = ln(1 + ) + .

    Заметим, рассмотренный интеграл можно вычислить, и применяя только замену переменной. Для этого можно воспользоваться, например, уже вычисленным неопределенным интегралом (пример в п. 19.4).

    3*. Покажем, что для любого n = 1, 2, ...

Под n!!, n N, понимается произведение всех натуральных чисел, не превышающих n и имеющих ту же четность, что и число n:

(2n)!! = 24...(2n - 2)2n,
(2n + 1)!! = 135...(2n - 1)(2n + 1).

По определению 0!! = 1.
    Положив для удобства I₀ = dx = /2 и проинтегрировав по частям интеграл I_n при n > 2, имеем

I_n = sinⁿ x dx = sin^n-1 x d(-cos x) = -sin^n-1 x cos x + (n - 1)sin^n-2 x cos² x dx =
                                                  = (n - 1)sin^n-2 x (1 - sin² x) dx = (n - 1)I_n-2 - (n - 1)I_n,

откуда

Заметим, что

Поэтому при n = 2k + 1, т. е. при нечетном n,

а при n = 2k, т. е. при четном n,

Равенство интегралов sinⁿ x dx и cosⁿ x dx сразу получается с помощью замены переменных
x = /2 - t, 0 < t < /2. Таким образом, формулы (26.4) доказаны. Из них легко получается формула Валлиса

В самом деле, проинтегрировав по отрезку [0,/2] неравенства

sin²ⁿ⁺¹x < sin²ⁿ x < sin^2n-1x,   n = 1, 2, ...,

получим

sin²ⁿ⁺¹x dx < sin²ⁿ x dx < sin^2n-1x dx,

т. е.

Отсюда в силу формул (26.4) имеем

Если ввести обозначения

то неравенства (26.11) можно записать в виде

где

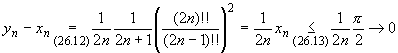при n,

и, следовательно, (x_n - y_n) = 0, т. е. длины отрезков [x_n, y_n], содержащих точку /2, стремятся к нулю, а это означает, что

x_n = y_n = /2.

Равенство x_n = /2 в силу первой формулы (26.12) и представляет собой формулу Валлиса.

Формула замены переменной  Оглавление  Понятие площади плоского множества