19.4. Формула замены переменной

    Познакомимся в заключение этого параграфа с двумя свойствами неопределенного интеграла, весьма полезными, в частности, для вычисления интегралов. Пусть функции f(x) и (t) заданы соответственно на промежутках _x и _t, причем функция f отображает промежуток _t на промежуток _x, т. е.

и, следовательно, имеет смысл сложная функция f((t)), t _t.
    Пусть, кроме того, функция (t) дифференцируема на промежутке _t и ее производная не меняет знака
на _t, т. е. для всех t _t имеет место либо неравенство '(t) > 0, либо '(t) < 0, а следовательно (см. п. 15.1), функция (t) строго монотонна на промежутке _t. Тогда (см. п. 7.3) у функции (t) существует обратная однозначная функция ^-1(x), определенная на промежутке _x. В формулируемой ниже теореме будем предполагать, что все перечисленные условия выполняются.
    Теорема 1. Существование на промежутке _x интеграла

и существование на промежутке _t интеграла

равносильны, и имеет место формула

Эта формула называется формулой замены переменной в неопределенном интеграле: переменная x заменяется переменной t по формуле x = (t). Если в формуле (19.15) в обеих частях равенства перейти к переменной t по формуле x = (t), то, меняя местами левую и правую части равенства, получим

    Иначе говоря, сделав сначала подстановку (t) = x, а затем взяв интеграл или сначала взяв интеграл, а потом сделав указанную подстановку, получим один и тот же результат.
    Формула (19.16) обычно называется формулой интегрирования подстановкой. Эту формулу можно записать также в виде

= .

Ее применение к вычислению интегралов состоит в том, что вместо интеграла вычисляется интеграл , а затем полагается x = (t). Формула замены переменной (19.15) и соответственно, формула интегрирования подстановкой (19.16) применяются тогда, когда интегралы, стоящие в их правых частях, в каком-то смысле проще интегралов, стоящих в их левых частях. Ниже, после доказательства теоремы, это будет пояснено на примерах.
Докажем сначала, что существование интегралов (19.13) и (19.14) равносильно, т. е. что равносильно существование первообразных у функции f(x) на промежутке _x и функции на промежутке _t.
    Пусть у функции f(x) на промежутке _x существует первообразная F(x), т. е.

В силу условия (19.12) имеет смысл сложная функция F((t)). Покажем, что она является на промежутке _t первообразной функции f((t))d(t)/dt. Действительно, по правилу дифференцирования сложных функций имеем

    Наоборот, пусть теперь функция f((t))d(t)/dt  имеет первообразную. Обозначим ее Ф(t):

В силу условий, которым удовлетворяет функция , обратная к ней функция ^-1 дифференцируема во всех точках промежутка _x, и имеет место формула (см. п. 10.6)

Покажем, что функция Ф(^-1(x)) является на промежутке _x первообразной для функции f(x). В самом деле,

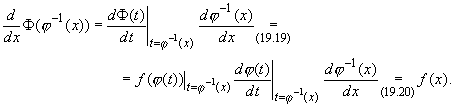
Итак, интегралы (19.13) и (19.14) одновременно существуют или нет. При этом

F(x) + С,	(19.21)
F((t)) + С	(19.22)

а так как

то

F(x) + СF((t)) + С = .

    Примеры.
    1^o. Вычислим с помощью формулы замены переменной (19.13) интеграл

,    -1 < x < 1.

Сделав замену переменной x = sin t, -/2 < x < /2, получим

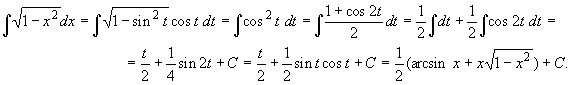
Аналогично вычисляется и интеграл , только здесь целесообразно положить x = sh t:

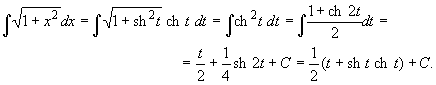
    В полученном выражении надо вернуться к переменной x. Имеем sh t = x, ch t = (1 + sh²t)^1/2 = (1 + x²)^1/2. Переменную же t найдем из уравнения x = sh t, т. е. из уравнения x = (e^t - e^-t)/2. Из него следует, что y = e^t удовлетворяет квадратному уравнению y² - 2xy - 1 = 0 и, следовательно, e^t = x + (1 + x)^1/2 (другой корень указанного квадратного уравнения отрицателен, а e^t принимает только положительные значения), откуда t = ln (x + (1 + x)^1/2). В результате окончательно получим

    2^o. Вычисление интегралов с помощью формулы подстановки (19.16) целесообразно, например, применять к интегралам вида . Применив в них подстановку (x) = u, получим

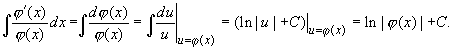
К такому типу интегралов относится интеграл

    Иногда, прежде чем применить метод интегрирования подстановкой, приходится проделать некоторые преобразования подынтегральной функции:

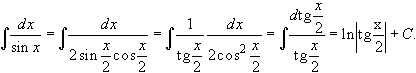
Табличные интегралы  Оглавление   Формула интегрирования по частям