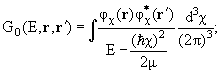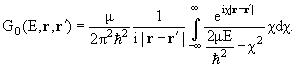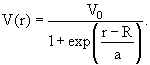Раздел I. Потенциальное рассеяние
Лекция 1. Стационарная теория потенциального рассеяния. Общие положения
§ 1.1. Постановка задачи. Интегральное уравнение для волновой функции. Асимптотическое условие
Методы современной квантовой теории столкновений принято разделять на две категории
− стационарные и нестационарные.
Внешнее различие между этими двумя подходами велико. Оно касается и
того, как формулируется задача, и математического аппарата и, наконец,
области непосредственного практического применения. В первом случае она
очень широка и включает разнообразные задачи, относящиеся к
столкновениям атомных частиц, ядерным реакциям, взаимодействию
элементарных частиц. Во втором случае область практического применения
теории гораздо уже. Нестационарная теория столкновений используется чаще
всего при решении особых задач, связанных с трактовкой специально
поставленных экспериментов. Кроме того, в отличие от стационарной теории
здесь по существу нет таких стандартных теоретических приемов, которые
были бы взяты «на вооружение» непосредственно экспериментаторами.
Тем не менее, между стационарной и нестационарной теориями
столкновений нет принципиальных различий, а, следовательно, и
какого-либо принципиального разделения сфер их действия. Мы покажем, что
стационарная теория столкновений со всеми ее привычными атрибутами − фазами рассеяния, борновским приближением, формфакторами и т.п.
− вытекает из строгой формулировки задачи столкновения, которая в
квантовой механике, как и в классической механике, дается изначально в рамках нестационарной теории. Другими словами,
стационарная теория столкновений − это особый математический метод,
«рецепт» решения задач теории столкновений, который технически очень
удобен и физически нагляден. Вместе с тем надо учитывать и то, что
современная квантовая физика все чаще сталкивается с задачами, где видна
потребность в разработке других, «прямых» методов нестационарной
теории, позволяющих непосредственно проследить за эволюцией состояний
квантовых систем в процессах столкновений.
Мы построим изложение следующим образом. Сначала, отправляясь от
интуитивных соображений, сформулируем основные положения стационарной
теории столкновений − сперва применительно к задаче потенциального
рассеяния, а затем и к разнообразным задачам о столкновениях с
составными системами. По ходу разработки конкретных методов теории мы
будем не только демонстрировать их успешное применение, но и
останавливаться на трудностях, условностях стационарной теории. В
заключительной лекции первого раздела курса будет сделано «сшивание»
стационарного и нестационарного подходов.
Начнем с простейшей задачи о рассеянии частиц неподвижным силовым
центром. Пусть V(r) − потенциальная энергия взаимодействия частиц с
центром, μ − масса частицы. Наша цель − найти дифференциальное сечение
рассеяния dσ/dΩ при условии, что на центр из бесконечности падает
плоскопараллельный пучок частиц с заданной начальной скоростью v0 =
n0v0.
Вспомним, как решается эта задача в классической механике. При t =
−∞ для каждой частицы падающего пучка задается прицельный параметр b. В общем случае это двумерный вектор в плоскости, перпендикулярной
направлению n0. При рассеянии сферически-симметричным или аксиально-симметричным (относительно направления падающих
частиц) потенциалом задача характеризуется аксиальной симметрией; в
таком случае достаточно указать модуль вектора b = |b|. Уравнения
движения позволяют найти для каждого значения b траекторию движения
частиц:
r = r(t). Ее асимптотика при t → +∞ указывает направление
вылета рассеянной частицы n, т.е. в общем случае, полярный G и
азимутальный ср углы рассеяния. Установив зависимость n = n(b), мы
вычисляем дифференциальное сечение рассеяния dσ/dΩ.
В квантовой механике нет траекторий движения частиц. Процесс
рассеяния описывается волновой функцией, которая при использовании
стационарной теории столкновений есть решение стационарного уравнения
Шредингера:
 ψ(r)
= Eψ(r). ψ(r)
= Eψ(r). |
(1.1) |
В рассматриваемой задаче r − это пространственная координата частицы,
а гамильтониан  − оператор, представляющий собой сумму оператора
кинетической энергии частицы
− оператор, представляющий собой сумму оператора
кинетической энергии частицы
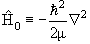 и потенциальной энергии ее взаимодействия с силовым центром и потенциальной энергии ее взаимодействия с силовым центром
 = V(r): = V(r):
Все взаимодействия, с которыми мы будем иметь дело, исчезают на
больших расстояниях от силового центра. Примем уровень потенциальной
энергии на бесконечности за начало отсчета полной и потенциальной
энергии частицы:
Таким образом, область, в которой V(r) > 0, соответствует отталкиванию, a V(r) < 0
− притяжению частицы силовым центром.
При Е > 0 уравнение (1.1) не имеет квадратично интегрируемых
решений. Вместе с тем важнейшим исходным положением квантовой механики
является положение о том, что только квадратично интегрируемые функции
описывают реальные состояния физических систем (см. [1, с.6]). Таким
образом, решения стационарного уравнения Шредингера, с которыми имеет
дело стационарная теория столкновений, играют с физической точки зрения
лишь вспомогательную роль, и их связь с реальными состояниями частицы,
испытывающей столкновение, нам еще предстоит выяснить (см. лекцию 7).
Подставляя (1.2) в (1.1), перепишем уравнение Шредингера в виде
( 0
− E)ψ(r) = - 0
− E)ψ(r) = - ψ(r). ψ(r). |
(1.4) |
Вместе с этим уравнением нам придется рассматривать и соответствующее
однородное уравнение, решения которого мы будем обозначать как φ(r):
( 0
− E)φ(r) = 0. 0
− E)φ(r) = 0. |
(1.5) |
Частным случаем решения φ(r) является плоская волна:
Не будучи квадратично интегрируемой, функция (1.6) не описывает
какого-либо реального состояния частицы; в стационарной теории
столкновений мы будем пользоваться ею для описания плоскопараллельного
стационарного потока частиц с заданным импульсом р = ћk (в дальнейшем
мы будем просто говорить - «с импульсом k»). Заметим, что при выбранной
нами нормировке функции (1.6) удовлетворяют следующему соотношению
(«условие полноты»):
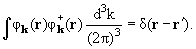 |
(1.7) |
Будем искать решение уравнения (1.4), описывающее процесс рассеяния,
исходя из следующего физического требования: пусть на достаточно большом
расстоянии от силового центра, когда взаимодействием между частицей и
силовым центром можно пренебречь, волновая функция задачи рассеяния
представляет собой суперпозицию плоской волны (1.6) и расходящейся
сферической волны:
| φk(r)|r→∞ = eikr
+ расх. волна, |
(1.8) |
где k − импульс (волновой вектор) падающих частиц. Ниже мы покажем, что такое решение уравнения (1.4) действительно существует.
Для этого перейдем от дифференциального уравнения Шредингера (1.4) к эквивалентному интегральному уравнению
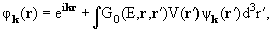 |
(1.9) |
где G0(E,r,r') − функция Грина, соответствующая оператору  0
и удовлетворяющая уравнению 0
и удовлетворяющая уравнению
(E −
 0)G0(E,r,r')
= δ(r − r') 0)G0(E,r,r')
= δ(r − r') |
(1.10) |
(мы будем называть G0(E,r,r')
функцией Грина свободного движения
частицы). В эквивалентности (1.4) и (1.9) легко убедиться, подставив
(1.9) в левую часть уравнения (1.4). При этом надо учесть связь между
энергией и импульсом свободной частицы:
В дальнейшем мы будем пользоваться также сокращенной записью уравнения (1.9):
ψk(r) = eikr
+
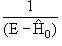  ψk(r), ψk(r), |
(1.12) |
или
ψk(r) = eikr
+ 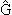 0(E) 0(E) ψk(r), ψk(r), |
(1.13) |
где
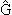 0(E) ≡ 0(E) ≡
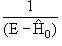
− гриновский оператор свободного движения частицы (являющийся, как видно из (1.9), интегральным оператором).
Интегральные уравнения (1.9), (1.13) для волновой функции задачи рассеяния носят название
уравнения Липпмана−Швингера.
Из всех возможных решений уравнения Липпмана− Швингера нам надо выбрать такие, которые удовлетворяют
асимптотическому условию (1.8). Как это сделать? Для ответа на этот
вопрос вычислим функцию Грина G0(E,r,r') и рассмотрим, как выглядит
она при r → ∞.
|