31.4. Свойства равномерно сходящихся последовательностей и рядов

    До сих пор при изучении последовательностей и рядов функций эти функции предполагались заданными на произвольном множестве X. Теперь мы перейдем к изучению свойств непрерывности, дифференцируемости и интегрируемости, в связи с чем множество X будет являться подмножеством числовой прямой.
    При изучении вопроса о непрерывности суммы ряда будем рассматривать ряды

u_n(x), где x X, u_n(x) C, n = 1, 2, ...

    Теорема 7. Если ряд равномерно сходится на некотором множестве и в какой-то точке этого множества все члены ряда непрерывны, то сумма ряда непрерывна в этой точке.
    Пусть ряд

равномерно сходится на множестве X, s(x) = u_n(x) - его сумма, а

- его частичные суммы. Зафиксируем произвольно > 0. Равномерная сходимость ряда (31.31) означает, что последовательность {s_n(x)} равномерно сходится на множестве X к функции s(x). Поэтому существует такой номер  > 0, что для всех точек x X выполняется неравенство

так как такое неравенство имеет место для всех номеров, начиная с некоторого. Зафиксируем указанный номер n.
    Функция s_n(x), являясь конечной суммой непрерывных (согласно условиям теоремы) в точке x₀ X функций u₁(x), u₂(x), ..., u_n(x), сама непрерывна в этой точке. Поэтому существует такое > 0, что для всех точек x X, удовлетворяющих условию x U(x₀;), выполняется неравенство

В силу сказанного для любой точки x X U(x₀;) имеем

|s(x) - s(x₀)| = |[s(x) - s_n(x)] + [s_n(x) - s_n(x₀)] + [s_n(x₀) - s(x₀)] <
< |s(x) - s_n(x)| + |s_n(x) - s_n(x₀)| + |s_n(x₀) - s(x₀)| /3 + /3 + /3 = .

Это и означает непрерывность функции s(x) в точке x₀. 
    Отметим, что в условиях теоремы в точке x₀ X для ряда u_n(x) возможен почленный переход к пределу, т. е.

un(x) =

un(x).

    Действительно, в силу непрерывности функций s(x) и u_n(x) в точке x₀ имеем
s(x) = s(x₀), u_n(x) = u_n(x₀) , n = 1, 2, ..., поэтому

un(x) = un(x) =

s(x) = s(x0) = un(x0) =

un(x).

    Заметим, что в теореме 7 условие равномерной сходимости ряда на множестве нельзя заменить условием только его сходимости на этом множестве. Это показывает пример 2 в п. 31.1: ряд (31.4) сходится на всей числовой прямой, его члены являются непрерывными на ней функциями, а сумма ряда - разрывная в точке x = 0 функция.
    Выше отмечалось, что изучение рядов равносильно изучению последовательностей (п. 30.1), поэтому каждое предложение о рядах можно перефразировать в соответствующее предложение о последовательностях. Будем рассматривать последовательности { f_n(x)}, x X R,  f_n(x) C, n = 1, 2, ... Теорема 7 в терминах последовательностей равносильна следующей теореме.
    Теорема 7'. Если последовательность функций равномерно сходится на некотором множестве и в некоторой точке множества все члены последовательности непрерывны, то и предельная функция последовательности непрерывна в этой точке. Заметим, что если

f_n f

и все функции непрерывны в точке x₀ X, то

 f_n(x) = f_n(x),

т. е. при сделанных предложениях предельные переходы при n и при xx₀ перестановочны. Действительно,

f_n(x) = f_n(x₀) = f(x₀) = f(x) =  f_n(x).

    Пример 3 в п. 31.2 еще раз подтверждает, что условие равномерной сходимости в теоремах 7 и  существенно.
    Теорема 8. Пусть функции u_n(x) R, n = 1, 2, ..., x [a,b], непрерывны на отрезке [a,b] и ряд

равномерно сходится на этом отрезке. Тогда, какова бы ни была точка x₀ [a,b], ряд

также равномерно сходится на отрезке [a,b] и

    Равенство (31.37) означает, что в условиях теоремы ряд (31.35) можно почленно интегрировать.
    В силу равномерной сходимости ряда (31.35) и непрерывности его членов на отрезке [a,b] его сумма

также непрерывна на этом отрезке (теорема 7), а следовательно, и интегрируема по Риману на отрезке [a,b], а поэтому и на любом отрезке с концами в точках x₀ [a,b] и x [a,b].
    Покажем, что ряд (31.36) равномерно сходится к функции

Как всегда, положим

а через _n(x) обозначим частичные суммы ряда (31.36):

Для любого x [a,b] имеем

|(x) - n(x)| s(t)dt - sn(t)dt < |s(t) - sn(t)|dt |rn(t)|dt < |rn(t)| dt  = |x - x0| |rn(t)| < (b - a)|rn(t)|.

(31.42)

Отсюда следует, что

|(x) - _n(x)| < (b - a)|r_n(x)|.

Из равномерной сходимости на отрезке [a,b] ряда (31.35) следует, что

 |r_n(x)| = 0.

Следовательно,

 |(x) - _n(x)| = 0.

что, согласно лемме 1, означает, что последовательность {_n(x)} равномерно на отрезке [a,b] сходится к функции (x), т. е. что ряд (31.36) равномерно сходится на указанном отрезке и что его сумма равна

(x) = u_n(t)dt.

Последнее равенство в силу (31.39) можно записать в виде

 s(t)dt = u_n(t)dt.

что согласно (31.38) равносильно равенству (31.37). 
    Перефразировка теоремы 8 в терминах последовательностей имеет следующий вид.
    Теорема 8'. Если последовательность непрерывных на отрезке [a,b] функций f_n(x), n = 1, 2, ..., равномерно сходится на этом отрезке к функции f(x), то, какова бы ни была точка x₀ [a,b], последовательность f_n(t)dt сходится равномерно на отрезке [a,b] к функции f(t)dt .
    Из этой теоремы следует, в частности, что

fn(t)dt = f(t)dt =

fn(t)dt,

т. е. что в данном случае можно переходить к пределу под знаком интеграла, или, коротко: в рассматриваемом случае предел интегралов равен интегралу от предела.

Замечание. Условия равномерной сходимости в теореме 8' являются существенными. Подтвердим это примером.
Функции f_n(x), 0 < x < 1, зададим для наглядности графически (рис. 126). Для любой точки x [0,1] имеем f_n(x) = 0 и, следовательно, 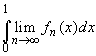= 0. При любом же n = 1, 2, ... интеграл f_n(x)dx = 1 равен площади треугольника AOB. Поэтому в этом случае

 f_n(x)dx = 1 0 = .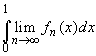

    Теорема 9. Пусть функции u_n(x) R, n = 1, 2, ..., непрерывно дифференцируемы на отрезке [a,b] и ряд, составленный из их производных:

равномерно сходится на отрезке [a,b]. Тогда если ряд

сходится хотя бы в одной точке x₀ [a,b], то он сходится равномерно на всем отрезке [a,b], его сумма

является непрерывно дифференцируемой функцией и

В силу формулы (31.45) последнее равенство можно записать в виде

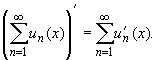
Таким образом, в условиях теоремы ряд (31.44) можно почленно дифференцировать.
    Положим

По теореме 8 этот ряд можно почленно интегрировать:

(мы использовали формулу Ньютона-Лейбница), причем ряд, стоящий в правой части равенства, в силу той же теоремы 8 равномерно сходится на отрезке [a,b].
    По условию теоремы числовой ряд u_n(x₀) сходится, причем, как и для всякого числового ряда, у него сходимость совпадает с равномерной сходимостью. Сумма двух равномерно сходящихся на отрезке [a,b] рядов [u_n(x) - u_n(x₀)] и u_n(x₀), т. е. ряд u_n(x), также, очевидно, равномерно сходится на отрезке [a,b]. В силу доказанной сходимости ряда (31.44) формулу (31.48) можно записать в виде

(t)dt = u_n(x) - u_n(x₀),

или (см. (31.45))

    Функция (t) является суммой равномерно сходящегося ряда непрерывных функций на отрезке [a,b] (см. (31.47)), и поэтому она сама непрерывна на этом отрезке, а тогда функция (t)dt непрерывно дифференцируема на [a,b] (см. п. 25.1) и

В силу формулы (31.49) это означает, что функция непрерывно дифференцируема и что

s'(x) (t)dt (x)u'_n(x).    

Для последовательностей функций аналогичная теорема выглядит следующим образом.
    Теорема 9'. Если последовательность непрерывно дифференцируемых на отрезке [a,b] функций f_n(x), n = 1, 2, .., сходится в некоторой точке x₀ [a,b], а последовательность их производных f'_n(x), n = 1, 2, ..., равномерно сходится на [a,b] к некоторой функции (x), то и последовательность {f_n(x)} сходится равномерно на отрезке [a,b] к непрерывно дифференцируемой функции f и f' = .
    Из рассуждений, проведенных при доказательстве теоремы 9, следует, что если функции f_n, n = 1, 2, .., непрерывно дифференцируемы и последовательность их производных {f'_n} равномерно сходится на отрезке [a,b], то условия:
    1) существует такая точка x₀ [a,b], что числовая последовательность {f_n(x₀)} сходится;
    2) f_nf;
    3) f_nf;
равносильны (то, что из условия 1) следуют условия 2) и 3), было доказано; что из 3) следует 1) - очевидно). Поэтому теорема 9 равносильна следующему утверждению.
   Если

f_nf   и  f'_n,

то существует производная f' и f' = , т. е. в этом случае предел производных равен производной от предела.
    В терминах рядов это утверждение (равносильное теореме 9) можно сформулировать следующим образом: если функции u_n(x) непрерывно дифференцируемы, а ряды u_n(x) = s(x) и u'_n(x) = (x) равномерно сходятся на отрезке [a,b], то у суммы ряда s(x) существует производная s'(x) и s'(x) = (x).
    Эти формулировки отражают сущность условий, при выполнении которых возможно почленное дифференцирование последовательностей и рядов. Но, конечно, на практике очень удобно, что сходимость последовательностей и рядов достаточно проверять лишь в одной точке и не доказывать их равномерную сходимость (конечно, равномерную сходимость последовательностей и рядов производных необходимо установить).
    Пример. Рассмотрим функцию

f(x) = 1/n^x,   x > 1,

называемую функцией Римана (ряд, стоящий в правой  части равенства, сходится при x > 1; см. (30.20)). Каково бы ни было > 1, ряд 1/n^x и ряд, получающийся его формальным дифференцированием, т. е. ряд
-ln n/n^x , равномерно сходятся на полуинтервале [,+). Это сразу вытекает в силу признака Вейерштрасса из неравенств

1/n^x < 1/,    0 < ln n/n^x < ln n/ < 1/,  0 < < - 1,

справедливых при фиксированном для достаточно больших n, и из сходимости рядов 1/, 1/. В силу теоремы 9 при любом x > имеет место равенство

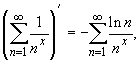
а поскольку > 1 было выбрано произвольно, то это равенство верно и при любом x > 1.

Специальные признаки равномерной сходимости рядов  Оглавление  Радиус сходимости и круг сходимости