|
(32.1) |
Степенным рядом называется ряд вида
|
(32.1) |
числа an ![]() C, n = 1, 2, …,
называются коэффициентами ряда (32.1).
C, n = 1, 2, …,
называются коэффициентами ряда (32.1).
С помощью замены переменного ![]() = z - z0
ряд (32.1) может быть преобразован к виду
= z - z0
ряд (32.1) может быть преобразован к виду
|
(32.2) |
Поэтому, как правило, мы ограничиваемся
рассмотрением рядов вида (32.2).
Теорема 1 (первая теорема
Абеля). Если степенной ряд (32.2) сходится
при z = z0, то при любом z таком, что
|z| < |z0|, ряд (32.2) сходится
абсолютно.
Следствие. Если ряд (32.2) расходится
в точке z0, то в любой точке z
такой, что |z| > |z0|, он
также расходится.
![]() Если ряд
Если ряд
|
(32.3) |
сходится, то![]() an
an![]() = 0, и потому существует
такая постоянная c > 0, что для всех n = 1,
2, … выполняется неравенство
= 0, и потому существует
такая постоянная c > 0, что для всех n = 1,
2, … выполняется неравенство
|an |
(32.4) |
Следовательно, при z0![]() 0 (в случае z0 = 0
утверждение теоремы очевидно и
бессодержательно, так как множество таких z,
что |z| < 0, пусто) имеем
0 (в случае z0 = 0
утверждение теоремы очевидно и
бессодержательно, так как множество таких z,
что |z| < 0, пусто) имеем
|anzn| = |an |
(32.5) |
|
и если |z| < |z0|, то ряд ![]() |z|/|z0|n
сходится, ибо является суммой бесконечно
убывающей геометрической прогрессии (ее
знаменатель |z|/|z0|n = |z|/|z0| < 1).
Поэтому по признаку сравнения сходимости рядов
из неравенства (32.5) следует, что сходится ряд
|z|/|z0|n
сходится, ибо является суммой бесконечно
убывающей геометрической прогрессии (ее
знаменатель |z|/|z0|n = |z|/|z0| < 1).
Поэтому по признаку сравнения сходимости рядов
из неравенства (32.5) следует, что сходится ряд ![]() |anzn|,
т. е. ряд (32.2) абсолютно сходится
(рис. 127).
|anzn|,
т. е. ряд (32.2) абсолютно сходится
(рис. 127). ![]()
Следствие сразу вытекает из теоремы:
если в точке z0 ряд (32.2) расходится, то
при |z| > |z0| он не может
сходиться в точке z, так как тогда бы он по
доказанной теореме сходился (и даже абсолютно) в
точке z0.
Рассмотрим степенной ряд (32.2). Он
заведомо сходится в точке z = 0. Обозначим
через X множество всех таких действительных
неотрицательных чисел x ![]() R,
что при z = x ряд (32.2) сходится.
Поскольку 0
R,
что при z = x ряд (32.2) сходится.
Поскольку 0 ![]() X,
то
X,
то
X![]()
![]() . Пусть
. Пусть
R = sup X. |
(32.6) |
Очевидно, 0 < R < +![]() . Неравенство |z| < R
задает на комплексной плоскости C
замкнутый круг радиуса R с центром в точке z = 0.
При R = 0 этот круг вырождается в точку z = 0,
а при R = +
. Неравенство |z| < R
задает на комплексной плоскости C
замкнутый круг радиуса R с центром в точке z = 0.
При R = 0 этот круг вырождается в точку z = 0,
а при R = +![]() превращается во всю комплексную плоскость.
превращается во всю комплексную плоскость.
Определение 1. Число R = sup X
(конечное или бесконечное) называется радиусом
сходимости ряда} (32.2), а круг {z: |z| < R}
- его кругом сходимости.
Теорема 2. Пусть R - радиус
сходимости ряда (32.2). Тогда если |z| < R,
то ряд (32.2) сходится абсолютно, если |z| > R,
то ряд (32.2) расходится, а если 0 < r < R,
то в круге {z: |z| < r} ряд
(32.2) сходится равномерно.
![]() Если R = 0,
то точек z
Если R = 0,
то точек z ![]() C таких, что |z| < R
нет. Если же 0 < R < +
C таких, что |z| < R
нет. Если же 0 < R < +![]() и z
и z ![]() C таково,
что |z| < R, то согласно определению
верхней грани из равенства R = sup X
следует, что существует такое x
C таково,
что |z| < R, то согласно определению
верхней грани из равенства R = sup X
следует, что существует такое x ![]() X, что |z| < x < R,
а так как по определению множества X во всех
его точках x ряд
X, что |z| < x < R,
а так как по определению множества X во всех
его точках x ряд ![]() an
xn сходится, то по первой теореме Абеля
он абсолютно сходится в точке z.
an
xn сходится, то по первой теореме Абеля
он абсолютно сходится в точке z.
|
Если R = +![]() , то точек z
, то точек z ![]() C
таких, что |z| > R, нет. Если же R < +
C
таких, что |z| > R, нет. Если же R < +![]() и z
и z ![]() C
таково, что |z| > R, то для любой точки
x такой, что R < x < |z|,
согласно определению R = sup X имеем x
C
таково, что |z| > R, то для любой точки
x такой, что R < x < |z|,
согласно определению R = sup X имеем x
![]() X, а поэтому в
силу определения множества X ряд
X, а поэтому в
силу определения множества X ряд ![]() an xn
расходится. Следовательно, в силу следствия из
теоремы 1 ряд (32.2) расходится в
рассматриваемой точке z.
an xn
расходится. Следовательно, в силу следствия из
теоремы 1 ряд (32.2) расходится в
рассматриваемой точке z.
Если теперь
0 < r < R, |
(32.7) |
то покажем, что ряд (32.2) сходится равномерно в круге |z| < r (рис. 128). Действительно, если |z| < r, то
|anzn| < |anrn|. |
(32.8) |
Из неравенства (32.7), согласно
вышедоказанному свойству радиуса сходимости,
вытекает, что ряд (32.2) при z = r
абсолютно сходится, т. е. сходится ряд ![]() |anrn, а тогда в
силу признака равномерной сходимости
Вейерштрасса (п. 31.2) из неравенства (32.8)
следует, что ряд (32.2) равномерно сходится в
круге {z: |z| < r}.
|anrn, а тогда в
силу признака равномерной сходимости
Вейерштрасса (п. 31.2) из неравенства (32.8)
следует, что ряд (32.2) равномерно сходится в
круге {z: |z| < r}. ![]()
Рассмотрим степенной ряд общего вида ![]() an(z - z0)n.
Он сходится или расходится в точке z тогда и
только тогда, когда соответственно сходится или
расходится в точке
an(z - z0)n.
Он сходится или расходится в точке z тогда и
только тогда, когда соответственно сходится или
расходится в точке ![]() =
z - z0 ряд
=
z - z0 ряд ![]() an
an![]() . Радиус сходимости R последнего
ряда называется и радиусом сходимости исходного
ряда
. Радиус сходимости R последнего
ряда называется и радиусом сходимости исходного
ряда ![]() an (z - z0)n.
an (z - z0)n.
При замене переменного ![]() = z - z0 кругу
сходимости {
= z - z0 кругу
сходимости {![]() : |
: |![]() | < R} ряда
| < R} ряда ![]() an
an![]() соответствует круг {z: |z - z0| < R}.
Он называется кругом сходимости ряда
соответствует круг {z: |z - z0| < R}.
Он называется кругом сходимости ряда ![]() an(z - z0)n.
an(z - z0)n.
Из теоремы 2 следует, что если R
является радиусом сходимости ряда ![]() an(z - z0)n,
то при |z - z0| < R этот
ряд абсолютно сходится, при |z - z0| > R
он расходится, а если 0 < r < R,
то в круге{z: |z - z0| < r}
ряд равномерно сходится.
an(z - z0)n,
то при |z - z0| < R этот
ряд абсолютно сходится, при |z - z0| > R
он расходится, а если 0 < r < R,
то в круге{z: |z - z0| < r}
ряд равномерно сходится.
Отметим, что из равномерной сходимости
ряда (32.1) в любом круге |z - z0| < R,
где 0 < r < R$, и
непрерывности каждого члена этого ряда следует,
что сумма каждого степенного ряда непрерывна
внутри его круга сходимости R > 0.
Действительно, для любого z, |z| < R,
можно выбрать такое R, что |z| < r < R.
В круге |z| < r рассматриваемый
ряд сходится равномерно, а так как его члены -
непрерывные функции, то его сумма также
непрерывна на этом круге, в частности в точке z (см.
теорему 7 в п. 31.4).
Примеры.
1. Рассмотрим ряд
|
32.9 |
Для исследования его абсолютной сходимости применим признак Даламбера (п. 30.4):
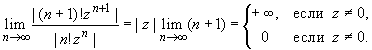
Следовательно, ряд (32.9) сходится только при z = 0,
а потому его радиус сходимости равен нулю: R =
0.
2. Радиус сходимости R ряда
|
(32.10) |
равен +![]() , так как
в п. 31.1 было показано,
что этот ряд сходится при любом z
, так как
в п. 31.1 было показано,
что этот ряд сходится при любом z ![]() C.
C.
3. Радиус сходимости суммы бесконечной
геометрической прогрессии
|
(32.11) |
равен 1, так как ряд (32.11) сходится при |z| < 1
и расходится при |z| > 1 (п. 30.1, 30.2). На границе {z: |z| = 1}
круга сходимости имеем |z| = 1 и,
следовательно, последовательность членов
ряда (32.11) не стремится к нулю, откуда явствует,
что во всех точках границы своего круга
сходимости ряд (32.11) расходится.
4. У ряда
|
(32.12) |
радиус сходимости также равен 1. Действительно, при |z| < 1 выполняется неравенство
|zn/n2| < 1/n2 |
(32.13) |
и, следовательно, согласно признаку
равномерной сходимости Вейерштрасса, ряд (32.12)
равномерно, а следовательно, и просто сходится.
При |z| > 1 имеем ![]() |zn|/n2
= +
|zn|/n2
= +![]() , т. е. не
выполняется необходимое условие сходимости ряда
(см. теорему 1 из п. 30.2), и,
таким образом, ряд (32.12) при |z| > 1
расходится.
, т. е. не
выполняется необходимое условие сходимости ряда
(см. теорему 1 из п. 30.2), и,
таким образом, ряд (32.12) при |z| > 1
расходится.
Отметим, что во всех точках границы
круга сходимости, т. е. при |z| = 1, в силу
того же неравенства (32.13) ряд (32.12) сходится.
5. Радиус сходимости R ряда
|
(32.14) |
можно найти, применив признак Даламбера: имеем
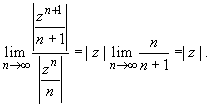
Поэтому ряд (32.14) сходится при |z| < 1
и расходится при |z| > 1. Таким образом, R = 1.
В точке z = 1 границы круга
сходимости ряд (32.14) превращается в гармонический
ряд и, следовательно, расходится, а при z = -1
получается сходящийся ряд ![]() (-1)n/n. Итак, у ряда (32.14) на
границе круга сходимости имеются как точки, в
которых он сходится, так и точки, в которых он
расходится. Разобранные примеры показывают, что
существуют степенные ряды, у которых радиус
сходимости равен нулю (ряд (32.9)), равен
конечному положительному числу (ряд (32.11)) и
равен бесконечности (ряд (32.10)). На границе
круга сходимости ряд может во всех точках
сходиться (ряд (32.12)), а может и сходиться в
одних точках и расходиться в других (ряд (32.14))
или расходиться во всех точках (ряд (32.11)).
(-1)n/n. Итак, у ряда (32.14) на
границе круга сходимости имеются как точки, в
которых он сходится, так и точки, в которых он
расходится. Разобранные примеры показывают, что
существуют степенные ряды, у которых радиус
сходимости равен нулю (ряд (32.9)), равен
конечному положительному числу (ряд (32.11)) и
равен бесконечности (ряд (32.10)). На границе
круга сходимости ряд может во всех точках
сходиться (ряд (32.12)), а может и сходиться в
одних точках и расходиться в других (ряд (32.14))
или расходиться во всех точках (ряд (32.11)).
Функции, раскладывающиеся
в степенные ряды, называются аналитическими.
Точнее, имеет место следующее
Определение 2. Функция f
называется аналитической в точке z0,
если в некоторой окрестности (см. п. 5.11) этой
точки функция f раскладывается в степенной
ряд:
f(z) = ![]() an(z - z0)n.
an(z - z0)n.
Поскольку в силу определения
окрестности точки все точки, достаточно близкие
к данной точке, принадлежат ее окрестности, то
радиус сходимости написанного ряда положителен.
Теорема 3* (вторая теорема
Абеля). Если R - радиус сходимости
степенного ряда (32.2), R < +![]() , и этот ряд сходится при z = R,
то он сходится равномерно на отрезке [0,R]
действительной оси.
, и этот ряд сходится при z = R,
то он сходится равномерно на отрезке [0,R]
действительной оси.
Следствие. Если ряд (32.2) сходится
при z = R, то его сумма
непрерывна на отрезке [0,R] действительной
оси.
![]() Доказательство
теоремы. Имеем
Доказательство
теоремы. Имеем
|
(32.15) |
причем, по условию теоремы ряд ![]() anRn сходится. Поскольку
этот ряд числовой, то его сходимость можно
рассматривать как равномерную сходимость на
отрезке [0,R]. Последовательность
anRn сходится. Поскольку
этот ряд числовой, то его сходимость можно
рассматривать как равномерную сходимость на
отрезке [0,R]. Последовательность
(x/R)n, n = 1, 2, ...,
ограничена на отрезке [0,R], ибо если 0 < x < R, то
0 < (x/R)n < 1,
и монотонна при любом x ![]() [0,R]. Следовательно, в силу
признака равномерной сходимости Абеля (п. 31.3*) ряд (32.2)
равномерно сходится на отрезке [0,R].
[0,R]. Следовательно, в силу
признака равномерной сходимости Абеля (п. 31.3*) ряд (32.2)
равномерно сходится на отрезке [0,R]. ![]()
Утверждение следствия вытекает из
непрерывности каждого члена ряда (32.2) на
отрезке [0,R] и доказанной равномерной
сходимости этого ряда на указанном отрезке.
Докажем еще одну лемму для степенных рядов в
комплексной области, которая будет использована
в следующем параграфе.
Лемма 1. Радиусы сходимости R, R1
и R2 соответственно рядов
| (32.16) | |
| (32.17) | |
| (32.18) |
равны:
| R = R1 = R2. | (32.19) |
Таким образом, ряды (32.17) и (32.18),
получающиеся из (32.16) соответственно с помощью
"формального интегрирования и
дифференцирования", имеют те же радиусы
сходимости, что и исходный ряд. Интегрирование и
дифференцирование названо здесь формальным,
поскольку для функций комплексного аргумента
эти операции у нас не были определены и они были
произведены так, как если бы an и z
были действительными числами.
![]() Из неравенства
Из неравенства
![]()
![]() zn+1
zn+1![]() =
= ![]() |z||anzn| < |z||anzn|
|z||anzn| < |z||anzn|
следует, что если в точке z абсолютно сходится ряд (32.16), то в этой точке абсолютно сходится и ряд (32.17), а это означает, что радиус сходимости R1 ряда (32.17) не меньше радиуса сходимости R ряда (32.16): R1 > R. Из неравенства же
|anzn| < n|anzn| = |nanzn-1||z|
следует, что если в точке z абсолютно
сходится ряд (32.18), то в этой точке абсолютно
сходится и ряд (32.16), т. е. R > R2.
Таким образом,
R1 > R > R2. |
(32.20) |
Покажем теперь, что
R2 > R1. |
(32.21) |
Возьмем какую-либо точку z![]() 0 внутри круга сходимости ряда (32.17)
и докажем, что в ней сходится ряд (32.18).
Поскольку |z| < R1, то существует
такое действительное число R, что
0 внутри круга сходимости ряда (32.17)
и докажем, что в ней сходится ряд (32.18).
Поскольку |z| < R1, то существует
такое действительное число R, что
|z| < r < R1. |
(32.22) |
Запишем абсолютную величину члена ряда (32.18) следующим образом:
|nanzn-1| = |
(32.23) |
Положим q = |z/r|. В силу условия (32.22) 0 < q < 1. Ряд
![]()
![]()
![]() =
= ![]()
![]() qn+1
qn+1
сходится (в этом легко убедиться, например, с помощью признака Даламбера). Поэтому последовательность его членов стремится к нулю и, следовательно, ограничена, т. е. существует такая постоянная c > 0, что для всех n = 0, 1, 2, ... выполняется неравенство
|
(32.24) |
Из (32.23) и (32.24) следует неравенство
|nanzn-1|< c![]()
![]() rn+1
rn+1![]() .
.
Поскольку r![]() R1,
то ряд
R1,
то ряд ![]()
![]() rn+1 абсолютно сходится, т. е.
сходится ряд
rn+1 абсолютно сходится, т. е.
сходится ряд ![]()
![]()
![]() rn+1
rn+1![]() , а поэтому по
признаку сравнения сходится и ряд
, а поэтому по
признаку сравнения сходится и ряд ![]() nanzn-1. Итак, из условия |z| < R1,
следует абсолютная сходимость ряда (32.18). Это и
означает выполнение неравенства (32.21). Из
неравенств (32.20) и (32.21) следует, что имеет место
равенство (32.19).
nanzn-1. Итак, из условия |z| < R1,
следует абсолютная сходимость ряда (32.18). Это и
означает выполнение неравенства (32.21). Из
неравенств (32.20) и (32.21) следует, что имеет место
равенство (32.19). ![]()
Свойства равномерно сходящихся последовательностей и рядов Оглавление Аналитические функции в действительной области